Раздел 9. Начала математического анализа.
Самостоятельная работа № 27.
Способы задания и свойства числовой последовательности.
Понятие о пределе последовательности. Бесконечно убывающая геометрическая последовательность и ее сумма
Цель: Знать определение последовательности и способы ее задания. Иметь понятие о пределе последовательности, бесконечно убывающей геометрической последовательности и ее сумме.
1. Изучив тему, письменно ответьте на вопросы:
10. Сформулируйте определение последовательности.
20. Перечислите способы задания последовательности.
30. Сформулируйте определение предела последовательности.
40. Дайте понятие бесконечно убывающей геометрической прогрессии и ее сумме.
2. Выполните письменно задания: №4.38(а,г), с. 138 из [2].
Литература: 1. М.Я. Пратусевич «Алгебра и начала математического анализа, 10кл., М., «Просвещение», 2014, гл.VII, §39, §40.
2. С.М. Никольский «Алгебра и начала математического анализа, 10 кл., М., «Просвещение», 2014, §4, п.4.5.
Самостоятельная работа № 28.
Производная и ее применение
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: создание презентации по заявленной теме.
Работа должна соответствовать методическим рекомендациям по созданию презентации.
Самостоятельная работа № 29.
Предел, связанный с числом 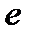
Цель: Знать основу появления числа 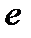 .
.
1. Изучив тему, письменно ответьте на вопросы:
10. Сформулируйте теорему о существовании предела:
а) ограниченной сверху неубывающей последовательности;
б) ограниченной снизу невозрастающей последовательности.
20. Что такое число 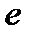
 (прим. 3, с. 141)?
(прим. 3, с. 141)?
2. Выполните письменно задание: №4.47(а,б,в).
Литература: С.М. Никольский «Алгебра и начала математического анализа», 10кл., М., «Просвещение», 2014, §4, п. 4.6.
Самостоятельная работа № 30.
Решение прикладных задач
Цель: Уметь применять определение производной и ее механический смысл к решению прикладных задач.
Методические рекомендации
Физический смысл первой производной.
Физический смысл производной заключается в том, что мгновенная скорость движения 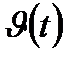 в момент времени t есть производная пути по времени, т.е.
в момент времени t есть производная пути по времени, т.е.
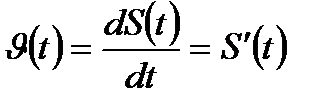
Физический смысл второй производной.
Ускорение прямолинейного движения в данный момент времени есть первая производная скорости по времени или вторая производная пути по времени.
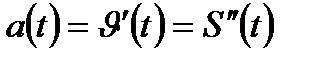
Пример.
1. Зависимость пути от времени при прямолинейном движении точки задана уравнением
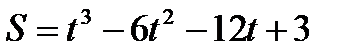 .
.
В какой момент времени ускорение движения точки будет равно 24 м/с2?
Решение.
а) Найдем скорость движения точки по формуле: 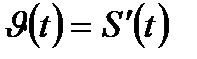
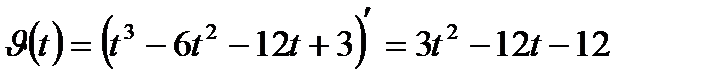
б) Найти ускорение движения точки по формуле: 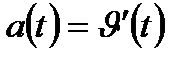
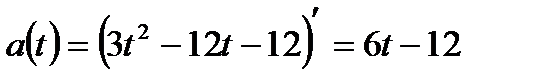
в) Из условия 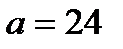 м/с2, найти момент времени:
м/с2, найти момент времени:
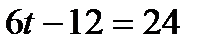
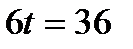
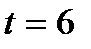 c
c
Ответ: 6 с.
v Правила дифференцирования и таблица производных основных функций.
Правила.
1. 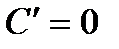 | 4. 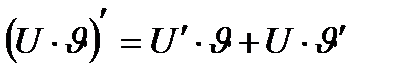 |
2. 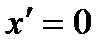 | 5. 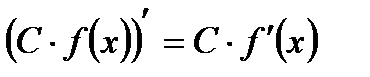 |
3. 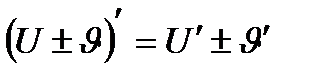 | 6. 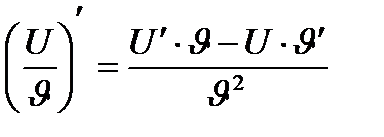 |
Производные основных элементарных функций.
1. 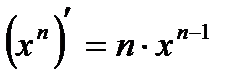 , , 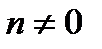 | 8. 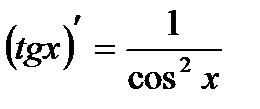 |
2. 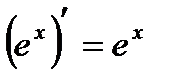 | 9. 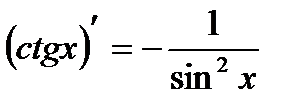 |
3. 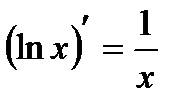 | 10. 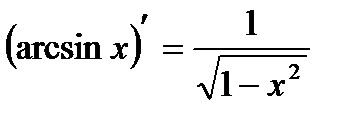 |
4. 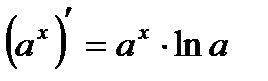 | 11. 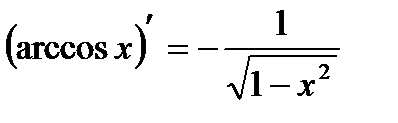 |
5. 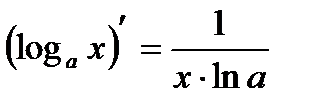 | 12. 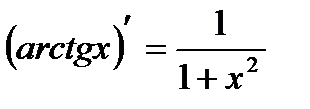 |
6. 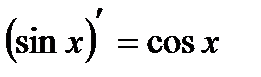 | 13. 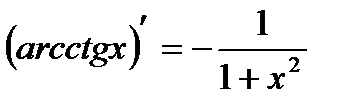 |
7. 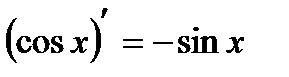 |
Используя методические рекомендации, выполните задания:
| 1 вариант | 2 вариант |
1. Тело движется вверх по закону 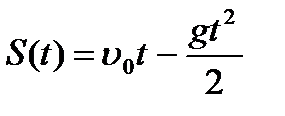 с начальной скоростью с начальной скоростью 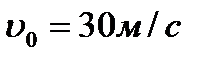 , , 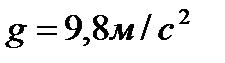 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 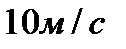 ? ? | 1. Тело движется вверх по закону 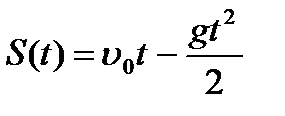 с начальной скоростью с начальной скоростью 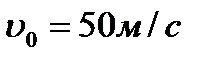 , , 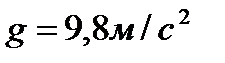 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 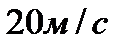 . . |
2. Найдите силу, действующую на тело массой 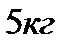 , движущееся по закону , движущееся по закону 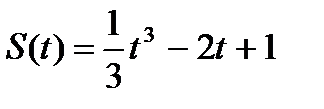 в момент времени в момент времени 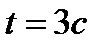 . . | 2. Тело массой 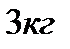 движется по прямой согласно уравнению движется по прямой согласно уравнению 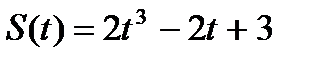 . Найдите действующую на него силу в момент времени . Найдите действующую на него силу в момент времени 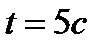 . . |
3. Определить кинетическую энергию точки, массой 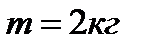 , движущейся по закону , движущейся по закону 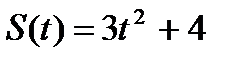 в момент времени в момент времени 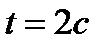 . . | 3. Определить кинетическую энергию точки, массой 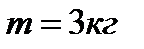 , движущейся по закону , движущейся по закону 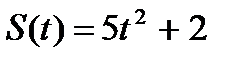 в момент времени в момент времени 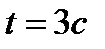 . . |
4.Точка движется по прямой по закону 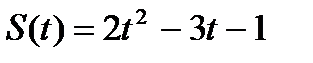 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 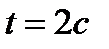 . . | 4. Точка движется по прямой по закону 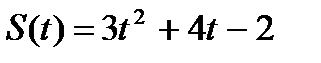 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 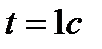 . . |
