Элементарные функции. Сложные функции
Цель: Знать определение функции, элементарной функции, сложной функции.
1. Изучив тему, письменно ответьте на вопросы:
10. Сформулируйте определение функции.
20. Какую функцию называют сложной?
30. Перечислите основные элементарные функции.
40. Какие функции называются элементарными?
2. Выполните письменно задания: №1.2; №1.4(а,б,в).
Литература: С.М. Никольский «Алгебра и начала анализа» 11кл., М., «Просвещение», 2014, с.3-4.
Самостоятельная работа № 19.
Изучение свойств функции
Цель: научиться исследовать функцию стандартными методами, строить ее график, научиться использовать преобразования для построения графика функции.
Методические рекомендации.
4.2. Преобразования графиков
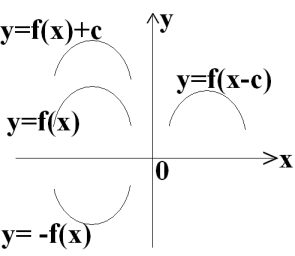
В общем виде: пусть имеем график некоторой функции 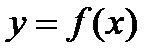 . Тогда, графики приведенных ниже функций получаются сдвигом исходного: (a > 0)
. Тогда, графики приведенных ниже функций получаются сдвигом исходного: (a > 0)
· 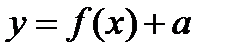 сдвиг графика вверх по оси У
сдвиг графика вверх по оси У
· 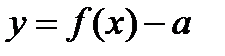 сдвиг графика вниз по оси У
сдвиг графика вниз по оси У
· 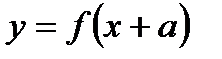 сдвиг графика влево по оси Х
сдвиг графика влево по оси Х
· 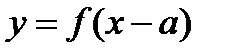 сдвиг графика вправо по оси Х
сдвиг графика вправо по оси Х
· 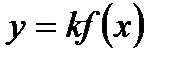 сжатие или растяжение графика от оси X
сжатие или растяжение графика от оси X
· 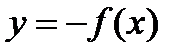 симметрия (отражение) графика относительно оси Х
симметрия (отражение) графика относительно оси Х
· 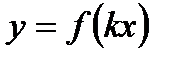 сжатие или растяжение графика от оси У(при к > 1 –сжат–е, при k < 1- растяжение)
сжатие или растяжение графика от оси У(при к > 1 –сжат–е, при k < 1- растяжение)
· 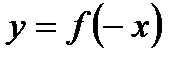 симметрия (отражение) графика относительно оси У
симметрия (отражение) графика относительно оси У
· 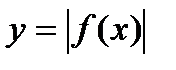 симметрия относительно оси Х
симметрия относительно оси Х
·  симметрия относительно оси У
симметрия относительно оси У
Исследование функций с помощью свойств.
1. Область определения функции - ОДЗ: функция может быть определенна на промежутках (a;b),[a;b],(−∞;+∞),(−∞;b),(a;+∞)
2. Исследование функции на четность, нечетность и периодичность: график четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
3. Нахождение точек пересечения графика функции с осями координат: на оси ОХ точка (x0;y0=f(x0)=0)
и на оси ОY точка (0;y0=f(0))
4. Нахождение промежутков знакопостоянства функции: промежутки, где функция принимает положительные или отрицательные значения, т.е. f(x)>0
или f(x)<0
5. Исследование поведения функции на бесконечности и в окрестности точек разрыва: точки разрыва определяют наличие вертикальной асимптоты, при исследовании поведения функции на бесконечности определяют наличие наклонной асимптоты или горизонтальной, как частный случай наклонной асимптоты.
1) 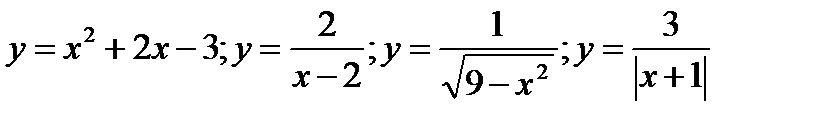 Найти область определения и множество значений функций:
Найти область определения и множество значений функций:
2) Исследовать на четность функции:
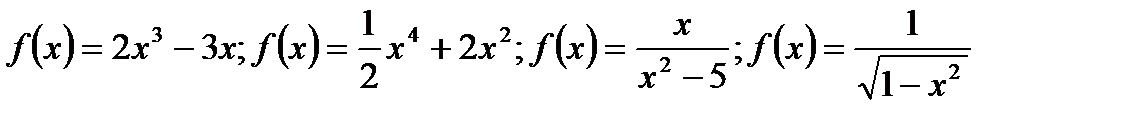
3) Используя график функции 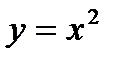 и преобразования графиков, построить графики функций:
и преобразования графиков, построить графики функций: 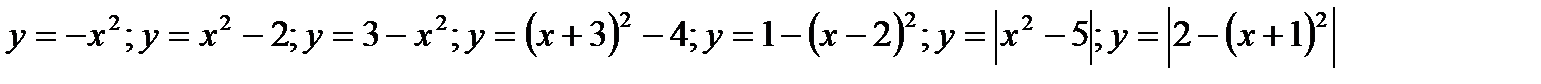
4) Найти область определения и множество значений функции, обратной данной: 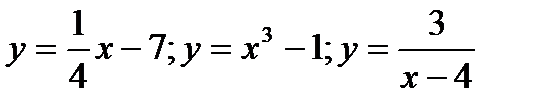
Самостоятельная работа № 20.
Примеры функциональных зависимостей
В реальных процессах и явлениях
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: подготовить реферат по предложенной теме.
Реферат должен быть выполнен с соблюдением методических рекомендаций по написанию реферата.
Раздел 8. Многогранники и круглые тела.
Самостоятельная работа № 21.
Правильные многогранники
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: создание презентации по заявленной теме.
Работа должна соответствовать методическим рекомендациям по созданию презентации.
Самостоятельная работа № 22.
Звездчатые многогранники
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: подготовить сообщение по предложенной теме.
Сообщение должно соответствовать методическим рекомендациям по подготовке сообщений.
Самостоятельная работа № 23.
Модели многогранников
Цель: Закрепить понятие многогранника при изготовлении моделей, используя развертки.
Форма самостоятельной деятельности: изготовление моделей многогранников.
Методические рекомендации
Одним из способов изготовления правильных многогранников является способ с использованием, так называемых, развёрток.
Если модель поверхности многогранника изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по нескольким рёбрам и развернуть так, что она превратится в модель некоторого многоугольника. Этот многоугольник называют развёрткой поверхности многогранника. Для получения модели многогранника удобно сначала изготовить развёртку его поверхности. При этом необходимыми инструментами являются клей и ножницы. Модели многогранников можно сделать, пользуясь одной разверткой, на которой будут расположены все грани. Однако в этом случае все грани будут одного цвета.
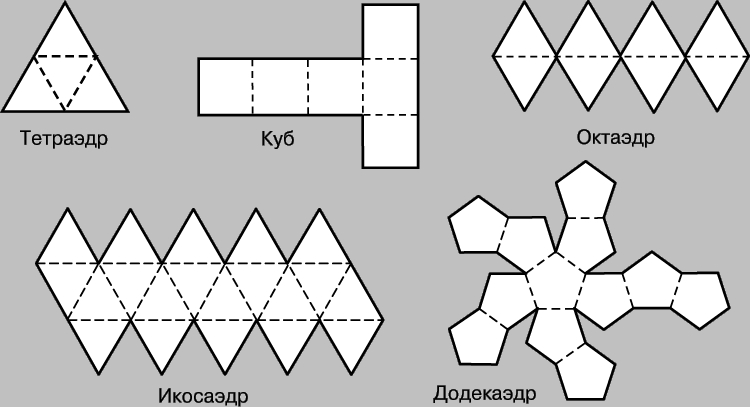
Используя методические рекомендации, изготовьте модели изученных вами многогранников.
Самостоятельная работа № 24.
Тела вращения
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: создание доклада по заявленной теме.
Работа должна соответствовать методическим рекомендациям по созданию доклада.
Самостоятельная работа № 25.
Модели тел вращения
Цель: Закрепить понятие тел вращения при изготовлении моделей, используя развертки.
Форма самостоятельной деятельности: изготовление моделей тел вращения.
Методические рекомендации
Одним из способов изготовления тел вращения является способ с использованием, так называемых, развёрток.
Если модель поверхности тела вращения изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по образующей, отделить основание и развернуть так, чтобы она превратится в модель некоторого многоугольника плюс круг. Эту фигуру называют развёрткой поверхности тела вращения. Для получения модели тела вращения удобно сначала изготовить развёртку его поверхности. При этом необходимыми инструментами являются клей и ножницы. Модели тел вращения можно сделать, пользуясь одной разверткой, на которой будут расположены все элементы.
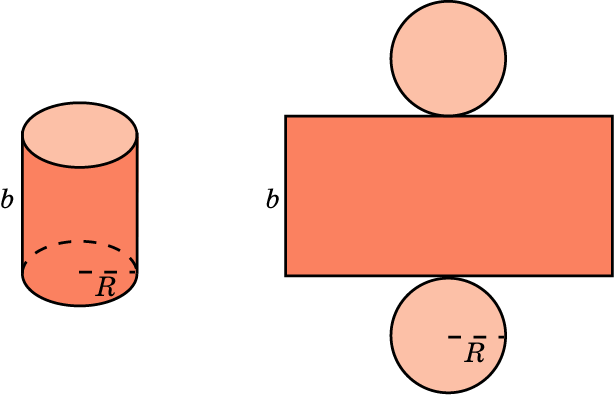
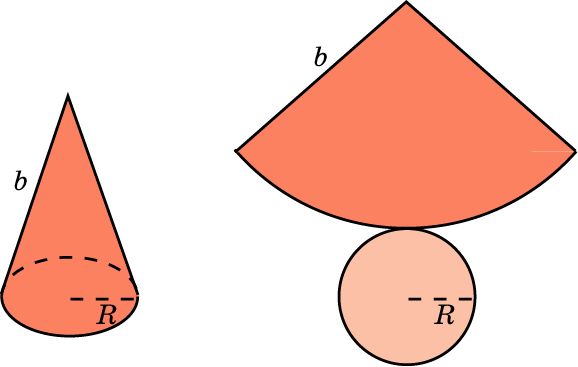
Используя развертки тел вращения, изготовьте их модели.
Самостоятельная работа № 26.
Объемы тел
Цель: Знать формулы для нахождения объемов многогранников и тел вращения.
Методические рекомендации
Основные формулы
| № п/п | Наименование многогранника | Изображение | Площадь боковой и полной поверхности |
| Куб | 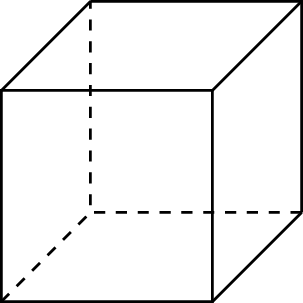 | 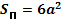 V=a3 V=a3 | |
| Прямоугольный параллелепипед |  | 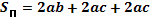 V=a*b*c V=Sосн*h V=a*b*c V=Sосн*h | |
| Призма | 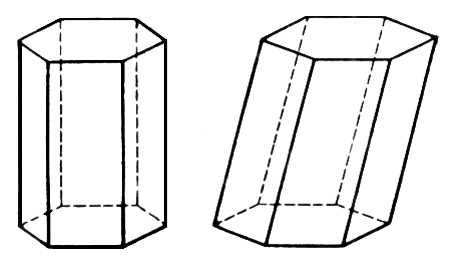 | 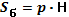 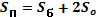 V=Sосн*h V=Sосн*h | |
| Пирамида | 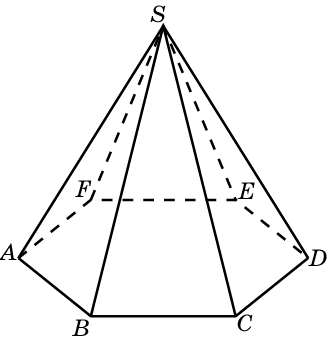 | 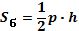 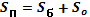 V=(1/3)*Sосн*h V=(1/3)*Sосн*h |
Теоретический материал
| № п/п | Наименование фигуры | Изображение | Формула площадей полной и боковой поверхности |
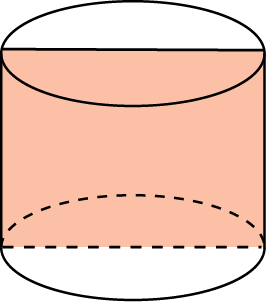
| Цилиндр |  | 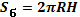 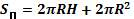 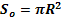 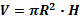 | |
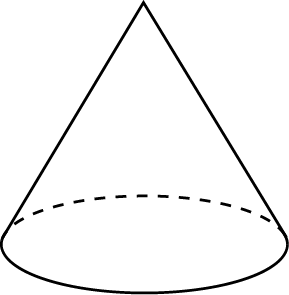
| Конус |  | 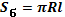 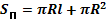 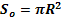 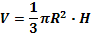 | |
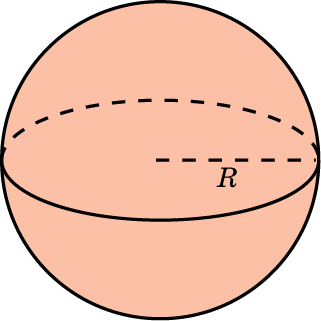
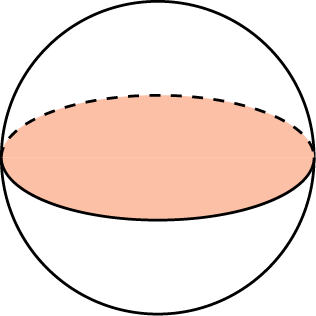
| Сфера, шар |  | 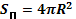 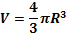 |
Используя методические рекомендации, решите задачи:
1 вариант
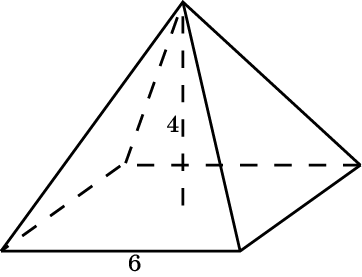
1. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6 см и высота 4 см.
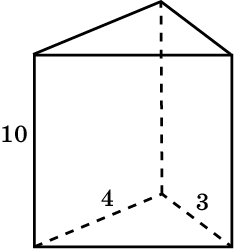
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите объем данной призмы.
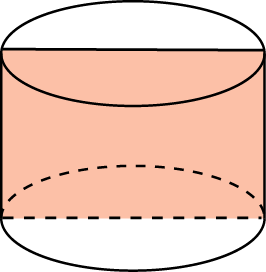
3. Площадь осевого сечения цилиндра равна 4 м2. Найдите объем цилиндра.
4. Высота конуса равна 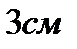 . образующая конуса составляет с плоскостью основания угол в
. образующая конуса составляет с плоскостью основания угол в  . Найти объем конуса.
. Найти объем конуса.
5. Площадь большого круга шара равна 3 см2. Найдите объем шара.
2 вариант
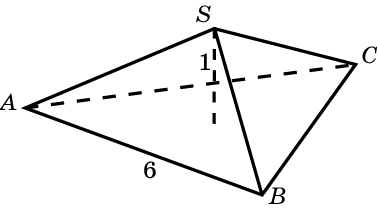
1. Найдите объём правильной треугольной пирамиды со стороной основания 6 см и высотой 1 см.
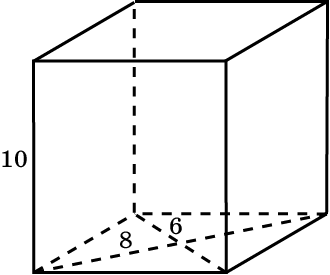
2. Найдите объем прямой призмы, в основании которой лежит ромб с диагоналями 6 см и 8 см и боковым ребром 10 см.
3. Осевое сечение цилиндра - квадрат. Площадь основания равна 1. Найдите объем цилиндра.
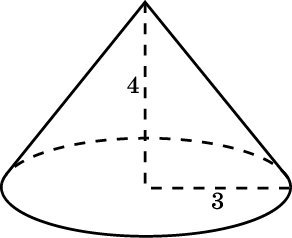
4. Радиус основания конуса равен 3 м, высота - 4 м. Найдите площадь объем конуса.
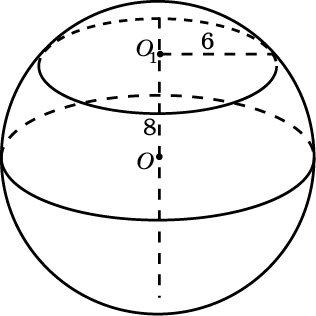
5. Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите объем шара.