Раздел 6. Элементы теории оптимизации
С.В. Акманова
Высшая математика
(избранные разделы)
МАГНИТОГОРСК
Министерство образования и науки Российской Федерации
ГОУВПО «Магнитогорский государственный университет»
Физико-математический факультет
Кафедра математического анализа
Светлана Владимировна Акманова
Высшая математика
(избранные разделы)
Магнитогорск
Рецензенты:
Кандидат технических наук, профессор кафедры
математического анализа МаГУ
Л.Е. Смушкевич
Доцент кафедры математического анализа МаГУ
Л.Н. Малышева
А40 Акманова С.В.
Высшая математика (избранные разделы): учебно-методическое пособие для студентов технологического факультета. – Магнитогорск : МаГУ, 2006. - 73 с.
В пособии рассмотрены основные теоретические положения, методы и правила решения задач по избранным вопросам высшей математики: нахождение безусловных и условных локальных экстремумов функций многих переменных, глобальных экстремумов функций многих переменных; элементы теории дифференциальных уравнений, включающие в себя подробное рассмотрение решения уравнений с разделяющимися переменными и линейных дифференциальных уравнений первого порядка; элементы теории вероятностей, а именно: классическое определение вероятности и связанные с ним понятия и теоремы, понятие случайной величины, закон распределения случайной величины, нормально распределенные случайные величины. Приведено большое количество подробно решённых задач, разъясняющих эти положения, методы и правила, предложены задания для самоконтроля, список рекомендуемой литературы.
Для студентов технологического факультета (в первую очередь, для студентов-заочников), а также для студентов университета, самостоятельно изучающих избранные разделы высшей математики.
ã Акманова С.В., 2006
Содержание
1. Предисловие…………………………………………………………………….4
2. Раздел 6. Элементы теории оптимизации...…………………………………..5
3. Раздел 7. Основные понятия теории обыкновенных дифференциальных уравнений…...……………………………………………………………………24
4. Раздел 8. Вероятность и статистика…………………………………………39
5. Рекомендуемая литература…………………………………………...............71
Приложение………………………………………………………………………72
Предисловие
Данное учебно-методическое пособие представляет собой практическое руководство студентов-заочников технологического факультета всех специальностей для выполнения индивидуальных домашних заданий, которые содержатся в методическом пособии Акмановой С.В., Смушкевича Л.Е. «Комплекс индивидуальных домашних заданий по курсу «Математика» для студентов заочного отделения технологического факультета» (Магнитогорск, 2004). Оно является продолжением изданных ранее пособий Акмановой С.В. «Руководство к решению индивидуальных домашних заданий по курсу «Математика» для студентов заочного отделения технологического факультета» и «Математика. Функции одной и нескольких действительных переменных».
В пособии представлены:
- основные теоретические сведения, охватывающие разделы 6, 7 и 8 указанного комплекса индивидуальных домашних заданий;
- способы и алгоритмы выполнения предложенных домашних заданий;
- задания для самоконтроля;
- список рекомендуемой литературы.
Предлагаемое руководство к решению задач будет также полезным и для студентов дневного отделения университета, начинающих изучать такие разделы математики, как «Элементы теории оптимизации», «Дифференциальные уравнения», «Теория вероятностей и математическая статистика».
Раздел 6. Элементы теории оптимизации
(Экстремум функции нескольких переменных)
Ранее нами было рассмотрено понятие экстремума функции одной действительной переменной. Введём понятие экстремума функции нескольких действительных переменных (на примере функции двух действительных переменных) и рассмотрим примеры выполнения заданий на его отыскание.
Задание 1. Исследовать на экстремум функцию.
Задания для самоконтроля
Исследовать на экстремум функции:
а) 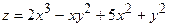 ;
;
б) 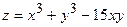 ;
;
в) 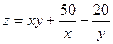 ;
;
г) 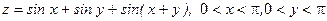 .
.
Ответы: а) 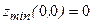 ;
;
б) 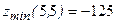 ;
;
в) 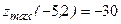 ;
;
г) 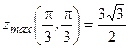 .
.
Итак, мы рассмотрели способы поиска безусловных локальных экстремумов функций, т.е. наибольших и наименьших значений функций, принимаемых ими в окрестностях отдельных точек из области определения функций. А теперь перейдём к рассмотрению вопроса о поиске глобальных экстремумов функций, т.е. наибольших и наименьших значений функций, принимаемых ими на области определения.
Задание 2. Найти наибольшее и наименьшее значения функции в замкнутой области.
На замкнутой области
1. Построить замкнутую область и определить её границу.
2. Найти критические точки функции внутри замкнутой области и вычислить значения функции в них.
3. Найти критические точки функции на границе замкнутой области и вычислить значения функции в них.
4. Найти значения функции в точках пересечения участков границы области (или на концах отрезков на границе области).
5. Выбрать из найденных значений функции наибольшее и наименьшее.
Примеры.
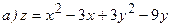 , область – треугольник, ограниченный прямыми
, область – треугольник, ограниченный прямыми 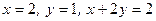 .
.
Решение.
1. Построим замкнутую область и выделим её границу.
|
|



|



|
|
|
|





|
|

|
2. Найдём критические точки функции внутри замкнутой области и вычислим значения функции в них.
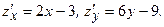
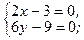
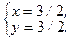
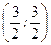 - критическая (стационарная) точка функции, однако
- критическая (стационарная) точка функции, однако 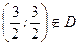 , т.е. внутри области
, т.е. внутри области 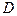 нет критических точек.
нет критических точек.
3. Найдём критические точки функции на границе замкнутой области и вычислим значения функции в них.
а) 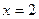 , тогда
, тогда 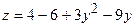 ,
,
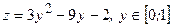 .
.
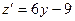 ,
, 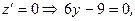
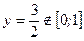 .
.
Значит, на указанном участке границы функция не имеет критических точек.
б) 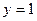 , тогда
, тогда 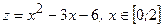 .
.
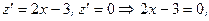
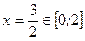 .
.
Значит, 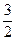 - критическая (стационарная) точка функции
- критическая (стационарная) точка функции 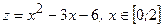 ;
;
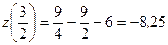 .
.
в) 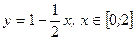 , тогда
, тогда 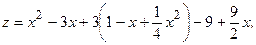
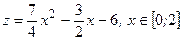 ,
,
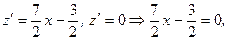
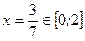 .
.
Значит, 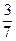 - критическая (стационарная) точка функции
- критическая (стационарная) точка функции 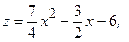
где 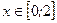 ;
; 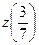 =
= 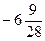 .
.
4. Найдём значения функции 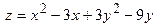 в точках
в точках 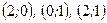 .
.
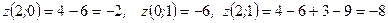 .
.
Таким образом, 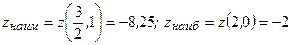 .
.
Ответ: 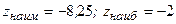 .
.
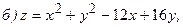 область – круг
область – круг 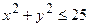 .
.
Решение.
|
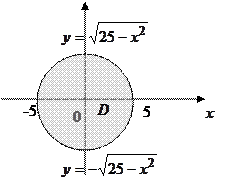 | |||||
| |||||
| |||||
2. Найдём критические точки функции внутри замкнутой области и вычислим значения функции в них.
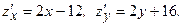 Рассмотрим систему
Рассмотрим систему
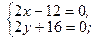
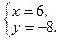
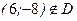 , значит, внутри замкнутой области функция не имеет критических точек.
, значит, внутри замкнутой области функция не имеет критических точек.
3. Найдём критические точки функции на границе замкнутой области и
вычислим значения функции в них.
Граница области (окружность) представима в виде двух дуг: 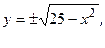
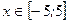 .
.
а) 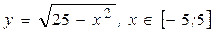 , тогда
, тогда 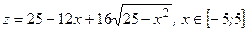 .
.
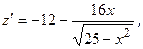
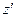 не существует при
не существует при 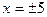 , а т.к.
, а т.к. 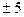 не являются внутренними точками отрезка
не являются внутренними точками отрезка 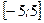 , то они не являются критическими точками функции
, то они не являются критическими точками функции 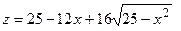 на отрезке
на отрезке 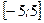 .
.
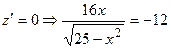 ,
,

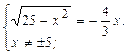 ;
;
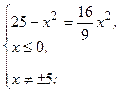
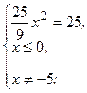
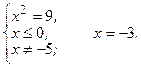
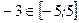 - критическая (стационарная) точка функции
- критическая (стационарная) точка функции 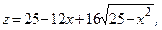
где 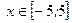 ;
; 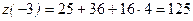 .
.
б) 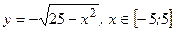 , тогда
, тогда 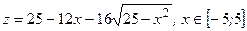 .
.
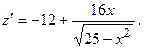 Аналогично,
Аналогично, 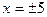 не являются критическими точками функции
не являются критическими точками функции 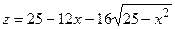 на отрезке
на отрезке 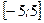 .
.
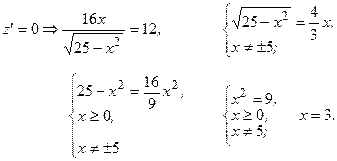
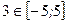 - критическая (стационарная) точка функции
- критическая (стационарная) точка функции 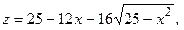
где 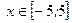 ;
; 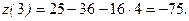
Заметим, что 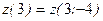 , где
, где 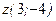 - значение функции
- значение функции 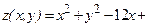
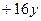 в точке
в точке 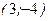 .
.
4. Найдём значения функции 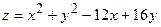 в точках (-5;0) и (5;0).
в точках (-5;0) и (5;0).
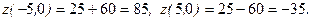
Значит, 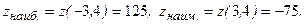
Ответ: 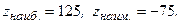
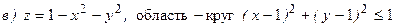 .
.
Решение.
|

|

 |


{Справка: 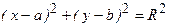 - каноническое уравнение окружности с центром в точке (
- каноническое уравнение окружности с центром в точке ( 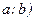 радиуса
радиуса 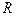 . Указанную окружность можно описать и параметрическими уравнениями вида:
. Указанную окружность можно описать и параметрическими уравнениями вида:
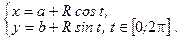 }
}
Таким образом, параметрические уравнения данной окружности имеют вид:
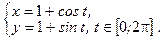
2. Найдём критические точки функции внутри области 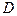 и вычислим значения функции в них.
и вычислим значения функции в них.
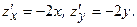
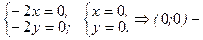 критическая точка функции.
критическая точка функции.
Однако, 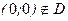 , т.е. внутри области
, т.е. внутри области 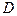 функция не имеет критических точек.
функция не имеет критических точек.
3. Найдём критические точки функции на границе области 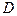 и вычислим значения функции в них.
и вычислим значения функции в них.
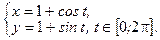
|
|

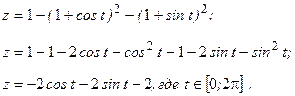
|
|
|



|
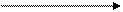
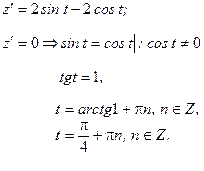
Поскольку 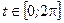 , то
, то 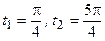 - критические точки функции на границе области.
- критические точки функции на границе области.
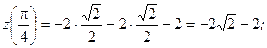
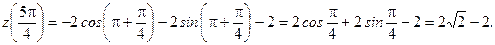
4. Найдём значения функции на концах отрезка 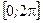 на границе области.
на границе области.
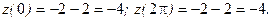
Значит, 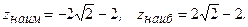
Ответ: 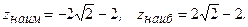
Задания для самоконтроля
Найти наибольшее и наименьшее значения функции:
а) 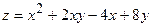 в прямоугольнике, ограниченном прямыми
в прямоугольнике, ограниченном прямыми 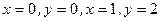 ;
;
б) 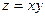 в круге
в круге 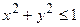 ;
;
в) 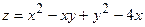 в замкнутой области, ограниченной прямыми
в замкнутой области, ограниченной прямыми 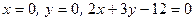 ;
;
г) 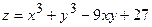 в квадрате
в квадрате 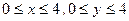 .
.
Ответы: а) 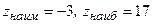 ;
;
б) 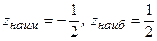 ;
;
в) 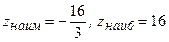 ;
;
г) 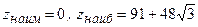 .
.
Помимо безусловных локальных экстремумов и глобальных экстремумов функций существуют и условные локальные экстремумы. Итак, рассмотрим следующее задание.
Задание 3. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
Задания для самоконтроля
Найти точки условного экстремума функции, используя метод множителей Лагранжа.
а) 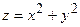 при
при 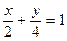 ;
;
б) 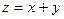 при
при 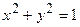 ;
;
в) 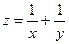 при
при 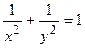 ;
;
г) 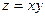 при
при 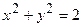 .
.
Ответы: а) 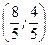 - точка условного минимума;
- точка условного минимума;
б) 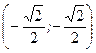 - точка условного минимума,
- точка условного минимума, 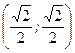 - точка условного максимума;
- точка условного максимума;
в) 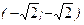 - точка условного минимума,
- точка условного минимума, 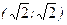 - точка условного максимума.
- точка условного максимума.
г) 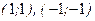 - точки условного максимума,
- точки условного максимума, 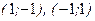 - точки условного минимума.
- точки условного минимума.
Раздел 7. Основные понятия теории обыкновенных дифференциальных уравнений
(Элементы теории дифференциальных уравнений)
Определение 1.Обыкновенным дифференциальным уравнением называется равенство, содержащее независимую переменную 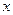 , неизвестную функцию
, неизвестную функцию 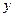 и её производные
и её производные 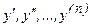 , т.е. имеющее вид
, т.е. имеющее вид
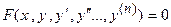 , (1)
, (1)
где 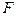 - функция действительных переменных
- функция действительных переменных 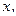
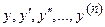 , принимающая также действительные значения.
, принимающая также действительные значения.
Определение 2.Порядком дифференциального уравнения называется максимальный порядок производной, который встречается в уравнении.
Так,
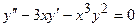 - дифференциальное уравнение второго порядка,
- дифференциальное уравнение второго порядка,
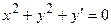 - дифференциальное уравнение первого порядка,
- дифференциальное уравнение первого порядка,
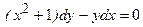 - дифференциальное уравнение первого порядка (
- дифференциальное уравнение первого порядка ( 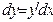 ),
),
(1) – общий вид дифференциального уравнения n-ого порядка. Дифференциа-льное уравнение 1 – ого порядка в общем виде запишется так: 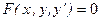 .
.
Например, 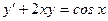 - дифференциальное уравнение первого порядка, где
- дифференциальное уравнение первого порядка, где 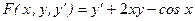 .
.
Определение 3.Решением дифференциального уравнения называется функция 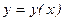 , обращающая при подстановке это уравнение в тождество.
, обращающая при подстановке это уравнение в тождество.
Например, для уравнения 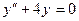 функция
функция 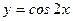 является решением, т.к.
является решением, т.к. 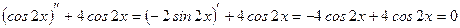 .
.
Определение 5.Общим решением дифференциального уравнения 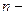 ого порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее
ого порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее  независимых произвольных постоянных, т.е. имеющее вид
независимых произвольных постоянных, т.е. имеющее вид
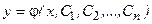 ,
,
где 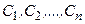 - независимые произвольные постоянные.
- независимые произвольные постоянные. 
Пример 1. 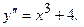 (*)
(*)
Решение.
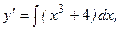
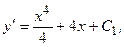
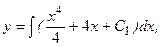
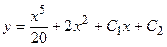 - общее решение уравнения (*).
- общее решение уравнения (*).
Определение 6.Частным решением дифференциального уравнения называется решение, получаемое из общего решения подстановкой вместо произвольных постоянных определённых чисел.
Так, 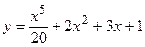 - частное решение уравнения (*), где
- частное решение уравнения (*), где 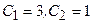 .
.
Определение 7.Общим интегралом дифференциального уравнения является его общее решение, выраженное в виде неявной функции.
Общий интеграл дифференциального уравнения n – ого порядка задаётся соотношением 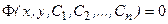 .
.
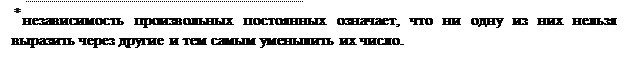
Например, 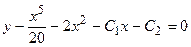 - общий интеграл уравнения (*). Его можно записать также в виде
- общий интеграл уравнения (*). Его можно записать также в виде 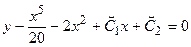 , где
, где 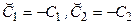 . Это объясняется тем, что из произвольности констант
. Это объясняется тем, что из произвольности констант 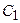 и
и 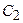 следует произвольность констант
следует произвольность констант 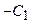 и
и 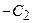 , для которых можно ввести новые обозначения, например,
, для которых можно ввести новые обозначения, например, 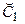 и
и 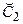 соответственно.
соответственно.
Общий интеграл дифференциального уравнения 1 – ого порядка задаётся соотношением 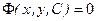 или
или 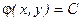 .
.
Пример 2. 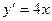 . (**)
. (**)
Решение.
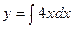 ,
,
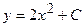 - общее решение уравнения (**),
- общее решение уравнения (**), 
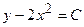 или
или 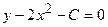 - общий интеграл уравнения (**).
- общий интеграл уравнения (**).
Задание 1.Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 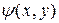 =С).
=С).
Задания для самоконтроля
Найти общее решение (общий интеграл) дифференциального уравнения:
1) 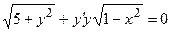 ; 5)
; 5) 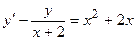 ;
;
2) 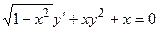 ; 6)
; 6) 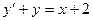 ;
;
3) 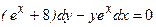 ; 7)
; 7) 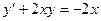 .
.
4) 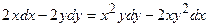 ;
;
Ответы: 1) 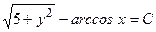 ; 5)
; 5) 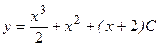 ;
;
2) 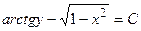 ; 6)
; 6) 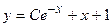 ;
;
3) 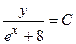 ; 7)
; 7) 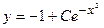 .
.
4) 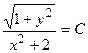 ;
;
Элементы комбинаторики
Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определённого типа можно составить из данных элементов. При этом под комбинациями понимаются группы элементов, отличающиеся одна от другой или порядком следования элементов, или самими этими элементами.
Комбинаторные задачи бывают самых разных видов, но большинство из них решается с помощью двух основных правил: правила произведения и правила суммы.
Правило произведения. Если объект 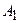 может быть выбран
может быть выбран 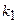 способами из имеющихся элементов, объект
способами из имеющихся элементов, объект 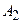 -
- 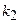 способами из оставшихся элементов, объект
способами из оставшихся элементов, объект 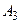 -
- 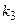 способами и т.д., то существует
способами и т.д., то существует 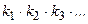 способов выбора совокупности объектов
способов выбора совокупности объектов 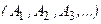 .
.
Пример. В группе 25 студентов. Сколькими способами можно выбрать в этой группе старосту, профорга и физорга?
Решение.
1. Старостой может быть каждый студент, тогда имеется 25 возможностей выбора старосты.
2. После выбора старосты осталось 24 студента, любой из них может быть профоргом. Следовательно, имеется 24 возможности выбора профорга.
3. Аналогично рассуждая, получаем 23 возможности выбора физорга.
Выбор старосты сочетается с выбором профорга и с выбором физорга.
Таким образом, всего возможностей выбора трёх должностей будет 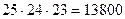 .
.
Ответ: 13800.
Правило суммы. Если множество 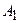 состоит из
состоит из 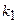 элементов,
элементов, 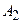 - из
- из 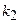 элементов, …, причём эти множества не имеют общих элементов, то выбор элемента либо из
элементов, …, причём эти множества не имеют общих элементов, то выбор элемента либо из 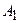 , либо из
, либо из 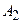 , … можно осуществить
, … можно осуществить 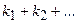 способами.
способами.
Пример. На книжной полке стоит 20 книг по алгебре, 12 – по теории вероятностей, 7 – по истории, 25 – по литературе и 6 – по геометрии. Сколькими способами можно выбрать книгу по математике?
Решение.
Всего книг по математике 20+12+6=38. Значит, имеется 38 способов выбора книги по математике.
Ответ:38.
Существуют три вида комбинаций, среди элементов которых нет повторяющихся, это: перестановки, размещения, сочетания.
Определение 11.Перестановки из  элементов – комбинации, состоящие из всех
элементов – комбинации, состоящие из всех  элементов и отличающиеся друг от друга лишь порядком следования элементов.
элементов и отличающиеся друг от друга лишь порядком следования элементов.
Обозначаются перестановки из  элементов -
элементов - 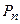 , при этом вычисляется число таких комбинаций по формуле
, при этом вычисляется число таких комбинаций по формуле
 |
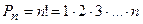
Полагаем, что 0!=1!=1.
Примеры.
1) Сколько пятизначных чисел можно составить из цифр 0,2,4,6,8, если числа в цифрах не повторяются.
Решение.
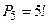 - число способов перестановки пяти цифр.
- число способов перестановки пяти цифр.
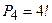 - число «пятизначных» чисел, начинающихся с «0». Тогда
- число «пятизначных» чисел, начинающихся с «0». Тогда 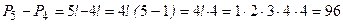 - число пятизначных чисел.
- число пятизначных чисел.
Ответ:96.
2) На трёх карточках написаны буквы У, К, Ж. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность, что получится слово «ЖУК»?
Решение.
Пусть  - событие «получится слово «ЖУК».
- событие «получится слово «ЖУК».
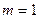 - число способов получения слова «ЖУК» из букв У, К, Ж;
- число способов получения слова «ЖУК» из букв У, К, Ж;
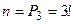 - число слов, которые можно получить из букв У, К, Ж.
- число слов, которые можно получить из букв У, К, Ж.
Значит, 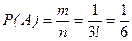 .
.
Ответ: 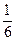 .
.
3) На один ряд из 7 мест случайным образом рассаживаются 7 учеников. Найдите вероятность того, что 3 определённых ученика окажутся рядом.
Решение.
Пусть  - событие, состоящее в том, что из 7 человек 3 определённых окажутся рядом. Найдём вероятность события
- событие, состоящее в том, что из 7 человек 3 определённых окажутся рядом. Найдём вероятность события  , используя классическое определение вероятности.
, используя классическое определение вероятности.
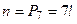 - общее число способов рассаживания 7 учеников,
- общее число способов рассаживания 7 учеников,
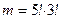 - число способов рассаживания 7 учеников, когда 3 определённых ученика окажутся рядом (3 ученика рассматриваются как один, тогда 1+4=5 учеников можно рассадить 5! способами, при этом внутри «тройки» ученики могут пересаживаться 3! способами; так как одни способы рассаживания нужно рассматривать в совокупности с другими, то по правилу произведения получим
- число способов рассаживания 7 учеников, когда 3 определённых ученика окажутся рядом (3 ученика рассматриваются как один, тогда 1+4=5 учеников можно рассадить 5! способами, при этом внутри «тройки» ученики могут пересаживаться 3! способами; так как одни способы рассаживания нужно рассматривать в совокупности с другими, то по правилу произведения получим 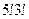 способов рассаживания учеников).
способов рассаживания учеников).
Значит, 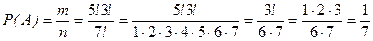 .
.
Ответ: 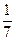 .
.
Определение 12.Размещения из  элементов по
элементов по 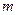 - комбинации, каждая из которых содержит
- комбинации, каждая из которых содержит 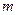 элементов из данных
элементов из данных  , при этом одна комбинация отличается от другой либо составом элементов, либо порядком расположения элементов.
, при этом одна комбинация отличается от другой либо составом элементов, либо порядком расположения элементов.
 Обозначение размещений из
Обозначение размещений из  элементов по
элементов по 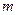 -
- 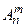 . Вычисляется число таких комбинаций по формуле
. Вычисляется число таких комбинаций по формуле
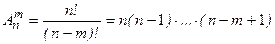 , где
, где 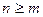
Примеры.
1) Сколько различных натуральных чисел можно записать с помощью цифр 0, 1, 2, 3, 4, если цифры в числах не повторяются?
Решение.
Поскольку числа – упорядоченные наборы цифр, отличающиеся один от другого либо порядком следования цифр, либо составом цифр, тогда для подсчёта количества однозначных, двузначных и других чисел нужно применять размещения.
Подсчитаем количество однозначных, двузначных, трёхзначных, четырёхзначных и пятизначных чисел, которые можно составить из данных цифр.
Количество однозначных чисел - 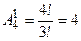 (это числа 1, 2, 3, 4).
(это числа 1, 2, 3, 4).
Количество двузначных чисел - 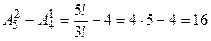 (так как
(так как 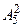 - число упорядоченных пар цифр, составленных из 0,1,2,3,4, то среди них могут быть числа вида 01, 02, 03, 04, которые не являются двузначными; количество таких чисел равно числу размещений
- число упорядоченных пар цифр, составленных из 0,1,2,3,4, то среди них могут быть числа вида 01, 02, 03, 04, которые не являются двузначными; количество таких чисел равно числу размещений 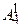 ).
).
Количество трёхзначных чисел - 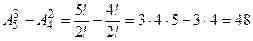 (
( 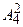 - число «трёхзначных» чисел, начинающихся с «0»).
- число «трёхзначных» чисел, начинающихся с «0»).
Количество четырехзначных чисел - 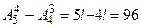 .
.
Количество пятизначных чисел - 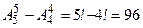 .
.
Итак, общее число натуральных чисел, записанных с помощью цифр 0,1, 2, 3, 4, равно: 4+16+48+96+96=260.
Ответ:260.
2) Из букв слова «событие», составленного с помощью разрезной азбуки, извлекаются наудачу и складываются друг за другом в порядке их извлечения 3 карточки (буквы). Какова вероятность получить при этом слово «быт»?
Решение.
Пусть  - событие, состоящее в том, что получено слово «быт».
- событие, состоящее в том, что получено слово «быт».
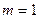 - число способов получения слова «быт» (это слово получится только
- число способов получения слова «быт» (это слово получится только  при условии: если из трёх извлечённых карточек первой будет буква «б», второй – «ы», третьей – «т»).
при условии: если из трёх извлечённых карточек первой будет буква «б», второй – «ы», третьей – «т»).
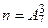 - общее число способов извлечения трёх карточек из семи.
- общее число способов извлечения трёх карточек из семи.
Тогда 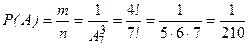 .
.
Ответ: 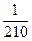 .
.
3) Числа 1,2,3,4,5 написаны на 5 карточках. Наудачу последовательно вынимаются 3 карточки, и вынутые таким образом цифры ставятся слева направо. Чему равна вероятность того, что полученное таким образом трёхзначное число окажется чётным?
Решение.
Виды трёхзначных чётных чисел, составленных из указанных цифр: 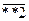 и
и 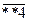 .
.
 - событие «получено чётное трёхзначное число».
- событие «получено чётное трёхзначное число».
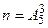 - общее число полученных трёхзначных чисел;
- общее число полученных трёхзначных чисел;
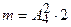 - число чётных трёхзначных чисел указанного выше вида, где
- число чётных трёхзначных чисел указанного выше вида, где 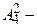 число способов заполнения ** в одной модели чётного числа (т.к. одна цифра уже задействована, то две цифры из четырёх с учётом порядка можно взять числом способов, равным
число способов заполнения ** в одной модели чётного числа (т.к. одна цифра уже задействована, то две цифры из четырёх с учётом порядка можно взять числом способов, равным 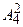 ).
).
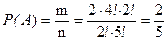 .
.
Ответ: 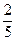 .
.
Определение 13.Сочетания из  элементов по
элементов по 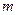 - комбинации, каждая из которых содержит
- комбинации, каждая из которых содержит 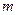 элементов из данных
элементов из данных  , при этом одна комбинация отличается от другой лишь составом элементов, но не порядком расположения элементов.
, при этом одна комбинация отличается от другой лишь составом элементов, но не порядком расположения элементов.
 Обозначение сочетаний из
Обозначение сочетаний из  элементов по
элементов по 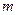 -
- 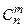 . Вычисляется число таких комбинаций по формуле
. Вычисляется число таких комбинаций по формуле

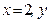
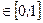 ; б)
; б) 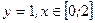 ; в)
; в) 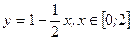 .
. 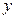
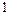
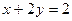
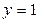
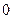
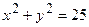 , т.е.
, т.е. 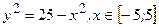 . Она представима в виде двух дуг
. Она представима в виде двух дуг 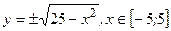 .
. 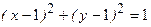 . Это каноническое уравнение окружности.
. Это каноническое уравнение окружности.