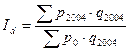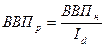Коэффициент автокорреляции Езекиэла и Фокса

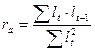, -1 ≤ r_q ≤ 1

Близость значения коэффициента к нулю означает отсутствие автокорреляции. Если величина близка к единице – наличие автокорреляции в остатках.

Критерий Дарвина-Уотсона

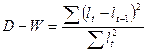
Между критерием Дарвина-Уотсона и коэффициентом автокорреляции существует соотношение:

D-W ≈ 2(1 – r_a)

Исходя из этого соотношения:

если в остатках нет автокорреляции (то есть r_a =0), то D-W = 2

если в остатках фиксируется полная положительная корреляция, то D-W = 0

если r_a = -1 , то D-W = 4

0 ≤ D-W ≤ 4

Близость к нулю и к четырем – присутствие автокорреляции в остатках от трендовой модели, к 2 – отсутствие.

Чтобы избежать субъективности оценок, обычно пользуются таблицами критерия D-W. По таблицам исходя из длины динамического ряда (числа уровней в динамическом ряду) и числа факторов в уравнении тренда находят границы критерия D-W₁ и D-W₂.

D-W_факт < D-W₁ - автокорреляция в остатках присутствует

D-W_факт > D-W₂ - автокорреляция в остатках отсутствует

D-W₁ ≤ D-W _факт ≤ D-W₂ - ситуация неопределенности, что требует дальнейшее исследование ряда и в частности построение ряда в условиях увеличения длины ряда.

40. Автокорреляция в рядах динамики. Понятие временного лага.

Автокорреляция в динамических рядах – зависимость между уровнями ряда или зависимость между исходным динамическим рядом и тем же рядом, но смещенным на определенный временной интервал, называемый лагом.

Лаг – временной интервал, разделяющий зависимые уровни.

Исходный		Смещенные ряды
ряд
lag = 1 lag = 2
yt
y1	yt-1
y2	y1	yt-2
y3	y2	y1
…	…	…
yn	yn-1	yn-2
	yn	yn-1
		yn

Наличие автокорреляции в рядах динамики оценивается на основе коэффициентов автокорреляции, которые строятся и рассчитываются аналогично коэффициентам парной корреляции

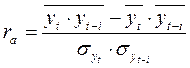, где

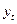– уровни исходного ряда

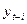– уровни смещенного ряда

i – временной лаг

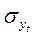– среднеквадратическое отклонение, рассчитанное на основе значений исходного ряда

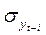- среднеквадратическое отклонение, рассчитанное на основе значений смещенного ряда

Величина лага определяет порядок коэффициента:

если lag = 1, то говорят о коэффициенте автокорреляции первого порядка

если lag = 2, то говорят о коэффициенте автокорреляции второго порядка

…

Если n > 20 и рассчитывается коэффициент автокорреляции первого порядка, то , .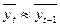

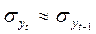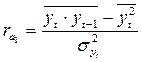
Чем больше величина лага и чем меньше число уровней в изучаемом ряду, тем больше разница в значениях средних уровней и стандартных отклонений коррелируемых рядов.

Коэффициент автокорреляции, как и парный коэффициент, изменяется в пределах от -1 до 1.

Оценка существенности (статистической значимости коэффициента автокорреляции) осуществляется на основе t- статистики:

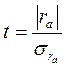
t_ф ≥ t_т - чтобы признать величину коэффициента автокорреляции статистически значимой.

Близость коэффициента автокорреляции к нулю будет свидетельствовать об отсутствии автокорреляции в уровнях рядов, к единице – о присутствии.

Наличие автокорреляции в рядах динамики (что характерно для экономических и социальных явлений) свидетельствует о присутствии тенденции в изучаемых рядах.

Если исследуемый временной ряд включает достаточное число временных рядов, то могут быть рассчитаны коэффициенты автокорреляции высоких порядков.

Последовательность коэффициентов автокорреляции r_a1, r_a2, r_a3, … , r_ai принято называть автокорреляционной функцией. На ее основе может быть изучена внутренняя структура динамического ряда, то есть можно получить ответы на вопросы: присутствует ли тенденция в изучаемом ряду, подвержены ли уровни ряда циклическим (сезонным) колебаниям; и указать период циклических колебаний, о котором свидетельствуют максимальные значения коэффициентов автокорреляции.

На основе функции автокорреляции строится график, который называется коррелограмма.

41. Авторегрессионные модели

Если установлено наличие автокорреляции в уровнях ряда, то тенденция изучаемого временного ряда может быть описана на основе уравнения авторегрессии.

Уравнение тренда: y = a + bt

Уравнение авторегрессии: y = a + by_t-i (в качестве фактора выступает предшествующий уровень).

Выбор уравнения авторегрессии осуществляется по аналогии с уравнением тренда и оценка его качества – по тем же критериям.

Величина i определяется исходя из порядка коэффициента автокорреляции, имеющего максимальное значение (если величина коэффициента статистически значима).

Если в изучаемом временном ряду отсутствуют циклические колебания, то коррелограмма отразит затухающую автокорреляционную функцию, так как чем выше порядок автокорреляции, тем меньше будет его значение. Поэтому в динамических рядах, построенных по данным годичных интервалов, как правило, максимальное значение имеет коэффициент автокорреляции первого порядка. Строится уравнение, в котором фактором выступает ряд, смещенный на один лаг.

Если получено удовлетворительное уравнение авторегрессии, на его основе может быть осуществлен прогноз, но следует помнить, что чем больше период упреждения, тем менее точен прогноз (так как уже на втором шаге прогноза в качестве фактора в уравнение подставляется уже спрогнозированная величина).

42. Анализ сезонности в рядах динамики.

Сезонность – устойчиво повторяющиеся (закономерные) колебания значений признака внутри года.

Динамика продаж Ford M.Company. Сезонные индексы и прогноз с учетом сезонной волны

год	квартал	объем продаж, млн. долл.	скользящая средняя объема продаж	отношение к скользящей средней	объем продаж с поправкой на сезонность
				0,93
				0,92
				1,04
				1,11
				0,91
				0,98
…	…	…	…	…	…
				1,1
				0,89
				1,05
				0,99
				1,07

Для определения индекса сезонности производится выравнивание исходного ряда по скользящей средней. Период скольжения равен пяти кварталам. Скользящая средняя рассчитывается по средней хронологической. То есть первое значение скользящей средней будет получено:

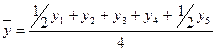
На основании полученных значений пятой графы по средней арифметической простой рассчитываются индексы сезонности для каждого квартала.

Индекс сезонности

Для 1 квартала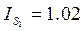

Для 2 квартала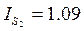

Для 3 квартала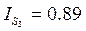

Для 4 квартала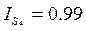

Индекс сезонности, например, второго квартала, говорит о том, что во втором квартале можно ожидать увеличение продаж в среднем на 9%.

На основе коэффициента сезонности может быть построен график сезонной волны.

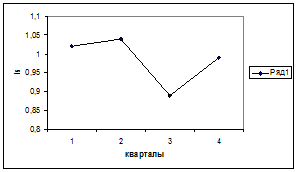
На основе значений индексов сезонности рассчитываются данные шестой графы таблицы. Строится трендовая модель, описывающая основную тенденцию изучаемого временного ряда. Уравнение тренда имеет вид:

Уравнение тренда – это уравнение, описывающее основную тенденцию объемов продаж компании, то есть построенное по теоретическим (выровненным) уровням, полученным на основе скользящей средней и без учета сезонной волны.

Прогноз основной тенденции осуществляется на основе уравнения тренда. Полученные данные корректируются с учетом соответствующих индексов сезонности.

Прогноз на основе тренда

	Без учета сезонной волны	С учетом сезонной волны
A

Значения первой графы – значения, полученные по уравнению тренда. Отражают поступательное увеличение объемов продаж по кварталам без учета сезонной волны.

Значения второй графы получают путем корректировки значений первой, то есть умножением на соответствующие индексы сезонности.

43. Корреляция рядов динамики.

На практике часто возникает необходимость изучения связей между двумя или несколькими динамическими рядами. Статистическим процедурам анализа всегда должен предшествовать теоретический анализ на основе положений экономической теории и знаний о тех процессах и явлениях, которые описываются имеющимися динамическими рядами. Этот анализ необходим чтобы избежать оценки так называемой ложной корреляции при реальном отсутствии зависимости между явлениями.

Если в изучаемых рядах существуют однонаправленные тенденции, то коэффициент корреляции получается завышенным. Если в изучаемых рядах присутствуют разнонаправленные тенденции, то значения коэффициентов корреляции получаются заниженными. Поэтому, если теоретически обоснованно наличие связи между временными рядами, то при статистической ее оценке следует исключить также с невыполнением одного из условий применения метода корреляционно-регрессионного анализа.

В динамических рядах, как правило, присутствует автокорреляция уровней, что говорит о невыполнении условия независимости наблюдений.

Статистикой разработано несколько вариантов исключения тенденции из временных рядов.

I В первую очередь возможно коррелировать не уровни рядов, а остатки от трендовых моделей. При этом выполняются следующие шаги:

1) строятся статистически значимые трендовые модели для каждого ряда;

2) определяются остатки от трендовых моделей;

3) оценивается наличие автокорреляции в остатках. Если в остатках автокорреляция присутствует, то опять строится модель и заново вычисляются остатки. Если в остатках автокорреляция присутствует, то на основе значений остатков рассчитывают показатели корреляции и строят модель.

II Коррелирование показателей, являющихся постоянными в трендовых моделях. Так, в условиях линейного тренда коррелируются цепные абсолютные приросты. Если тренд описывался экспонентой, коррелируются цепные коэффициенты роста. Если тренды в изучаемых рядах описаны с использованием разных функций, возможно коррелировать разные показатели.

III Переход от парной регрессии ко множественной регрессии путем прямого включения в уравнение связи фактора времени.

Математической статистикой доказано, что включение фактора времени аналогично коррелированию остатков от трендовых моделей.

Самый распространенный вариант ухода от автокорреляции.

При изучении зависимости между временными рядами следует учитывать возможность запаздывания изменения уровней другого временного ряда. При коррелировании таких рядов следует учитывать этот временной лаг.

44. Экстраполяционное прогнозирование. Расчет доверительных интервалов.

Получив удовлетворительную модель динамического ряда, можно осуществить прогнозирование поведения изучаемого временного ряда. Как правило, период упреждения не должен превышать ⅓ длины изучаемого ряда. В любом случае прогнозирование требует анализа условий существования изучаемого объекта.

Экстраполяция означает продление описанной тенденции в будущее.

Пример: 1) трендовая модель, описывающая динамику индексов потребительских цен

y = 99.7 + 1.8t

2) трендовая модель, описывающая динамику производства мяса в России

1983 – 1995гг

y = 9.7133 – 0.1593t – 0.0817t²

При благоприятных условиях на основе трендовой модели может быть получен так называемый точечный прогноз, который никогда не может сбыться. Поэтому точечный прогноз следует дополнить расчетом доверительных интервалов прогноза.

ŷ - ∆ ≤ ỹ ≤ ŷ + ∆ ,

где ỹ - точечный прогноз на основе трендовой модели, который рассчитан по уравнению тренда путем подставления в качестве фактора t порядкового номера временного периода, на который осуществляется прогноз.

∆ = t · S - предельная ошибка

Величина t в предельной ошибке берется исходя из заданного уровня вероятности в таблице Стьюдента.

Величина S – средняя квадратическая ошибка

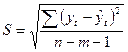
Получив доверительные границы, можем указать вероятность, с которой гарантируется, что прогнозируемая величина будет находиться в указанных пределах.

45. Статистические индексы, задачи, решаемые с помощью индексного анализа.

Индекс – относительный показатель, полученный как соотношение значений того или иного признака (экономического показателя) во времени, пространстве, в сравнении с каким-либо нормативом лил плановым уровнем.

Так как индекс – это всегда соотношение двух значений, то тому значению, которое сопоставляется, присваивается понятие показатель отчетного периода и рядом со значением показателя ставится 1 (единица). То значение показателя, с которым производится сравнение, называется базисным и рядом с ним ставится 0 (ноль).

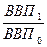
В индексном анализе существует ряд общепринятых обозначений:

q (или Q) – физический объем продукции или товара (в натуральном выражении);

p – цена единицы изделия;

z (иногда С) – себестоимость единицы изделия;

q∙p – стоимость товара, товарооборот;

q∙z – издержки производства;

t – трудоемкость единицы изделия;

w – выработка.

При использовании индексного анализа показателей социальной сферы могут быть использованы приведенные выше обозначения. При этом следует помнить, что необходимо различать количественные показатели и так называемые качественные (рассчитанные на ту или иную единицу). Деление на количественные и качественные показатели соответствует делению на первичные и вторичные признаки.

46. Индексы общие и индивидуальные.

По степени охвата элементов изучаемой совокупности различают индексы:

Индивидуальные (i)

Рассчитываются по отдельным элементам. Тот показатель, изменение которого оценивается, называется индексируемым, а соответствующий индекс отражает название показателя.

Индекс физического объема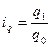

Так как в индексном анализе как правило проводится сравнение во времени, то эти индивидуальные индексы – показатели темпа роста.

Общие индексы (сводные, I)

Рассчитываются по всей совокупности элементов благодаря введению в индексы так называемых соизмерителей. Чаще всего в качестве соизмерителей используются цены, а также себестоимость и трудоемкость.

Общие индексы могут быть рассчитаны в виде агрегатных индексов и как индексы средние из индивидуальных.

47. Агрегатный индекс как основная форма индексов.

Агрегатный индекс товарооборота:

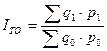
Агрегатный индекс выполняет две функции:

- объединяет изначально несоизмеримые элементы (синтетическая функция)

- позволяет оценить роль отдельных факторов в изменении сводного показателя (аналитическая).

Синтетическая функция реализуется благодаря введению показателя соизмерителя (веса) в агрегатный индекс.

Индекс товарооборота может быть разложен на две составляющие:

1)индекс физического объема, который позволит оценить роль изменения объемов продаж в изменении объема товарооборота в целом.

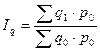
Индексируемой величиной является физический объем продаж, поэтому в числителе объем продаж берется на уровне отчетного периода, а в знаменателе – базисного, а вес (цена) остается неизменной (на уровне базисного периода). В целом числитель индекса – это экономический показатель, характеризующий фактический объем продаж в неизменных сопоставимых ценах. Знаменатель – товарооборот базисного периода (объем продаж).

2) индекс цен

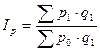
Данный индекс будет характеризовать изменение товарооборота за счет изменения цен на товары.

Произведение этих двух индексов – общий индекс товарооборота.

Ряд индексов, построенных по взаимосвязанным признакам, называют системой индексов. В частности индекс товарооборота равен произведению индексов физического объема и цен.

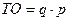
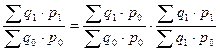
На основе полученных индексов можно рассчитать величины абсолютных изменений товарооборота, физического объема и цен

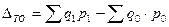- абсолютное изменение товарооборота.

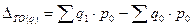
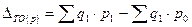
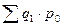- товарооборот отчетного периода в ценах базисного периода;

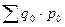- товарооборот базисного периода;

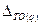- характеризует изменение объема продаж в сопоставимых ценах (то есть элиминируется влияние цен на изменение общего товарооборота);

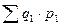- товарооборот отчетного периода;

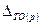- означает величину экономии/перерасхода населения за счет снижения/увеличения цен в отчетном периоде по сравнению с базисным периодом.

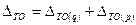
При построении индексов основной обсуждаемой проблемой является проблема выбора периода весов. Основной критерий выбора периода взвешивания – цель индексного анализа. Однако при построении системы индексов существует правило выбора периода весов: если индексируется количественный (первичный) признак, признак-вес берется на уровне базисного периода; если индексируется качественный (вторичный) признак, признак-вес берется на уровне отчетного периода.

Вторая система индексов (с точки зрения популярности применения на практике) связана с изучением изменения средних величин (средних показателей) и включает в себя индекс переменного состава, индекс постоянного состава и индекс структуры.

Общее изменение средней величины (например, средней цены) характеризуется индексом переменного состава

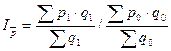
На изменение средней цены влияет изменение собственно цен, а также структура продаж (доля продаж по той или иной цене в общем объеме продаж).

Так как в индексном отношении структура берется за разные периоды времени, то индекс носит название индекса переменного состава.

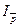может быть разложен на два составляющих индекса:

- индекс, который изменит изменение средней цены в результате изменения собственно цен при элиминировании влияния структурных изменений

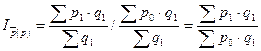- индекс постоянного состава.

- изменение средней цены в результате изменения структуры

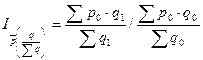- индекс струетуры

Индексируемый признак – структура продаж. Признак-вес – цена. Ее закрепление на уровне базисного периода позволяет элиминировать изменение цен на динамику средней цены.

Величина индекса структуры, большая 1 (>100%) будет свидетельствовать о том, что в отчетном периоде по сравнению с базисным увеличивается доля продукции с более высокой ценой.

Если индекс < 1 (<100%), то в отчетном периоде по сравнению с базисным увеличивается доля продукции с более низкой ценой.

На основе системы индексов также могут быть рассчитаны показатели в абсолютном выражении.

Абсолютный прирост или снижение средней цены (на сколько в абсолютном выражении выросла средняя цена по сравнению с базисным периодом) – это разность составляющий индексного отношения.

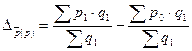
Абсолютное изменение цены за счет изменения структуры:

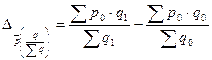
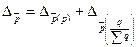
48. Индексы Ласпейреса и Пааше.

Индексы Ласпейреса и Пааше возникли в рамках решения проблемы построения индексов цен. В 1864г немецким статистиком и аналитиком Ласпейресом был предложен индекс цен, в котором признак-вес закрепляется на уровне базисного периода.

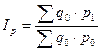- индекс Ласпейреса

В 1874г немецкий аналитик Пааше предложил индекс цен с использованием признака-веса на уровне отчетного периода

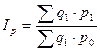- индекс Пааше

В настоящее время при исчислении индексов потребительских цен в большинстве экономически развитых стран используется индекс Ласпейреса.

При использовании индекса Ласпейреса постоянно необходимо отслеживать только изменение цен, поскольку физический объем продаж остается на уровне базисного периода. Так в европейских странах физический объем (структура, состав) остается неизменным в течении трех лет.

Несмотря на то, что методика и Ласпейреса и Пааше предполагалась только относительно индексов цен, в настоящее время любые индексы с использованием базисных весов называются индексами Ласпейреса, а с использованием отчетных весов – индексами Пааше.

,

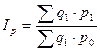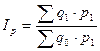
Идеальный индекс Фишера

Рассчитывается как средняя геометрическая величина из произведений индексов Ласпейреса и Паше

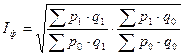
Затруднена экономическая интерпретация полученного индекса.

Идеальный индекс Фишера используется в международных сравнениях.

49. Правило выбора весов при построении системы индексов.

При построении индексов основной обсуждаемой проблемой является проблема выбора периода весов. Основной критерий выбора периода взвешивания – цель индексного анализа. Однако при построении системы индексов существует правило выбора периода весов: если индексируется количественный (первичный) признак, признак-вес берется на уровне базисного периода; если индексируется качественный (вторичный) признак, признак-вес берется на уровне отчетного периода.

Вторая система индексов (с точки зрения популярности применения на практике) связана с изучением изменения средних величин (средних показателей) и включает в себя индекс переменного состава, индекс постоянного состава и индекс структуры.

50. Индексы средние из индивидуальных.

Форма индексов средних из индивидуальных, широко используется для обобщения динамики цен на уровне стран.

Индексы средние из индивидуальных можно назвать показателями центральной тенденции (так как среднее значение – показатель центра распределения). Эти индексы также могут быть рассчитаны по методике Ласпейреса и Пааше.

Индексы цен средние из индивидуальных рассчитывают по средней взвешенной, в качестве весов используется доля расходов населения на приобретение того или иного товара или услуги в конкретном регионе или на конкретной территории в общем объеме затрат населения страны на приобретение данного товара (услуги).

Эти данные получают на основе обследования бюджетов семей. Доля расходов населения рассчитывается по отдельным группам товаров-представителей и по отдельным видам услуг.

Индексы средние из индивидуальных, рассчитанные по методике Ласпейреса с использованием признака-веса на уровне базисного периода, рассчитываются по средней арифметической взвешенной.

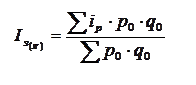
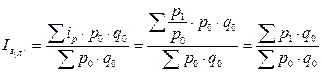
Если индексы средние из индивидуальных рассчитываются по методике Пааше (с использованием отчетных весов), то используется средняя гармоническая взвешенная

Специальный вид индексов, который используется для перевода показателей системы национальных счетов в сопоставимый вид. Например, пересчет ВВП из номинального вида в реальную величину. По экономической теории номинальный ВВП – это фактический объем производства ВВП в текущем году в текущих ценах, а реальный ВВП – фактический объем производства в ценах базисного периода.

,
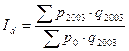