Средняя арифметическая простая

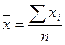, где

n – объем совокупности (число единиц в совокупности),

x_i – значение признака у i-ой единицы совокупности.

Среднее арифметическое – отношение объема признака к объему совокупности. Используется для расчета средних значений абсолютных показателей по несгруппированным данным.

Средняя арифметическая взвешенная

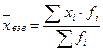, где

x_i – варианты значений признака,

f_i – частота повторений данного варианта.

Используется при расчете среднего значения абсолютных величин по сгруппированным данным, а также среднего значения относительных показателей при условии, что известен знаменатель исходной формулы усредняемого показателя.

Средние по относительным показателям рассчитываются только по средней взвешенной и никогда по средней простой.

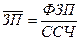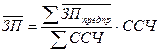, , где

ЗП – заработная плата,

ФЗП – фонд заработной платы,

ССЧ – средняя списочная численность рабочих.

Средняя гармоническая

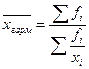
Средняя гармоническая используется для расчета среднего значения относительных величин при условии, что известен числитель исходной формулы усредняемого показателя.

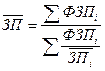
Средняя геометрическая

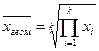
k - число сомножителей в подкоренном выражении

Степень корня = k

Средняя геометрическая используется для расчета средних темпов роста в анализе рядов динамики.

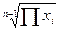- имеется в виду подсчет по всем единицам совокупности,

то есть k = n – 1.

Средняя квадратическая

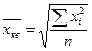(простая) → 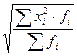(взвешенная)

Формула средней квадратической лежит в основе расчета дисперсии.

Свойства средней арифметической:

1. Произведение средней арифметической на сумму частот равно сумме произведения индивидуальных значений признака на соответствующие частоты.

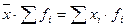
Среднее арифметическое – это значение признака, которое имела бы каждая единица совокупности при равномерном распределении общего объема признака совокупности.

1. Сумма отклонений индивидуальных значений признака от средней величины всегда равна нулю.

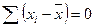
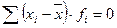
1. Сумма квадратов отклонений индивидуальных значений от средней величины всегда меньше суммы квадратов отклонений индивидуальных значений от любой другой произвольной величины.

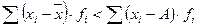
1. Если все индивидуальные значения увеличить или уменьшить на одну и ту же постоянную величину, то среднее арифметическое уменьшится или увеличится на эту же величину.
2. Если все частоты умножить или разделить на одно и то же постоянное число, то среднее не изменится.

9. Понятие вариации, показатели вариации.

Вариация – это различия в индивидуальных значениях признака у единиц совокупности. Вариация – основа развития различных систем (биологических, экономических).

От степени вариации признаков совокупности зависит типичность показателей центра распределения. Чем меньше вариация, тем в большей степени средняя выполняет роль характеристики типического уровня признака. Поэтому, как правило, расчет показателей центра распределения сопровождается расчетом показателей вариации.

Для оценки вариации существуют абсолютные и относительные показатели вариации.

Абсолютные показатели: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

1. размах вариации. Разность между максимальным и минимальным значением признаков совокупности.

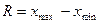
Характеризует на какую величину различаются между собой крайние значения изучаемого распределения.

Среднее линейное отклонение

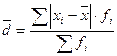, где

x_i - индивидуальное значение признака,

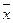- среднее значение по совокупности.

3. дисперсия

σ² =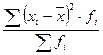

Показатель дисперсии в экономических исследованиях содержательно не интерпретируется, но благодаря своим свойствам широко используется в расчете многих статистических характеристик.