Метод простой итерации для решения СЛАУ

Применим метод простой итерации для решения системы уравнений

.

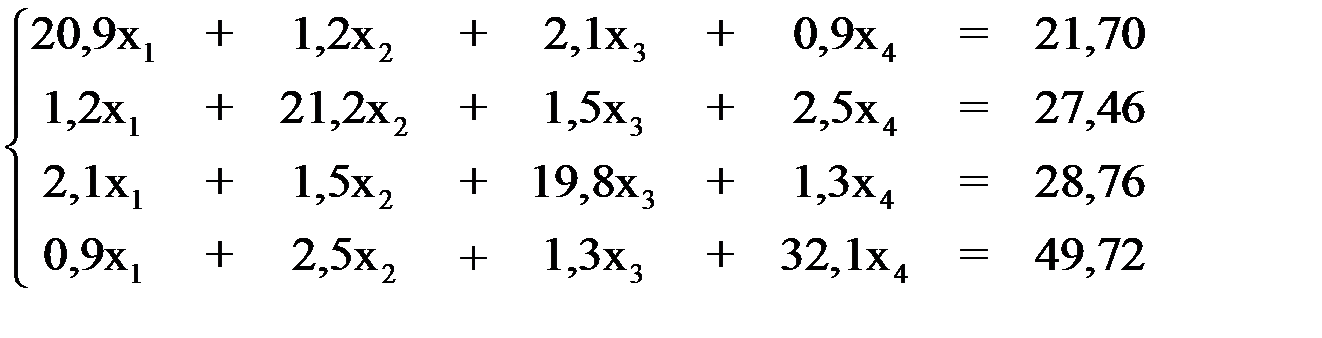Заметим, что метод простой итерации сходится, так как выполняется условие преобладания диагональных элементов:

, ,

, .

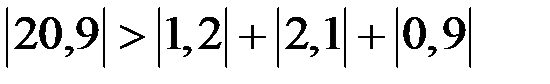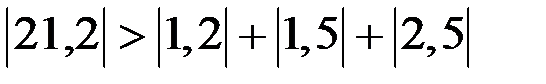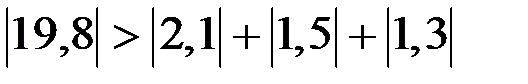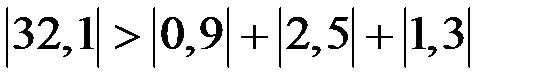Пусть требуемая точность 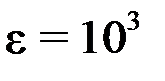. Вычисления будем проводить с четырьмя знаками после десятичной точки.

Приведем систему к виду:

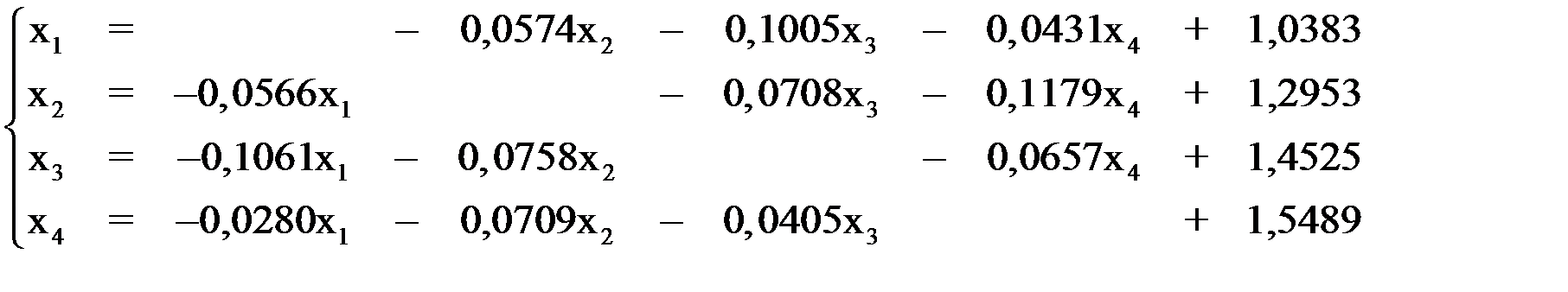
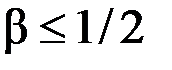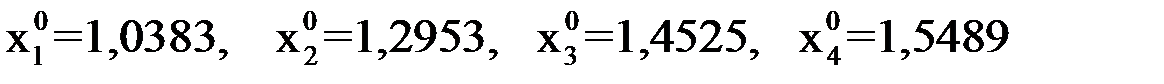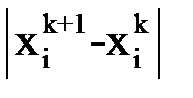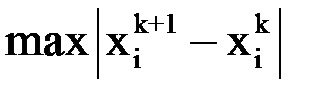Величина равна 0,1179, т. е. выполняется условие и можно пользоваться критерием окончания итерационного процесса (8). В качестве начального приближения возьмем элементы столбца свободных членов: . Вычисления будем вести до тех пор, пока все величины , , а следовательно, и не станут меньше .

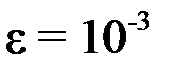Последовательно вычисляем:

при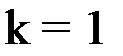

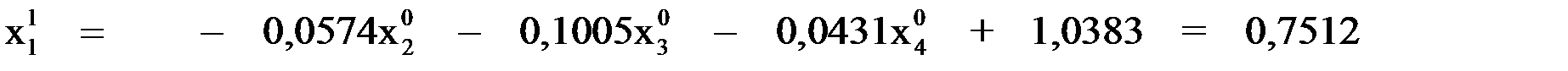
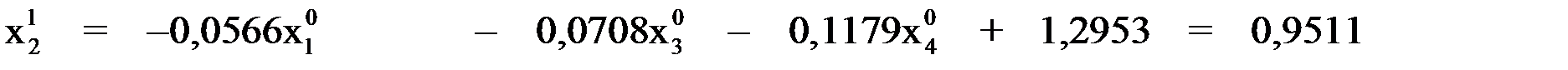
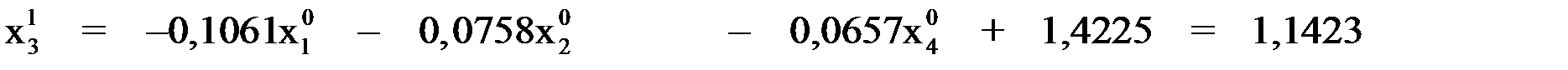
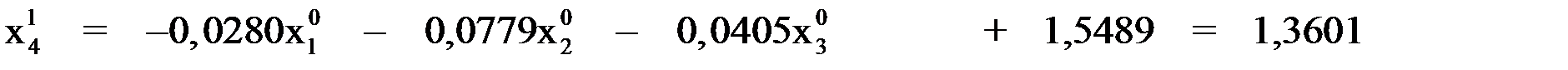
при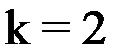

.

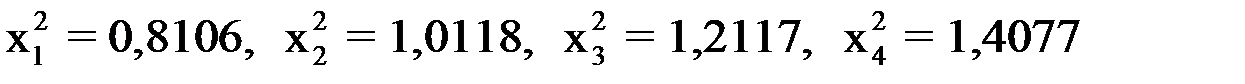при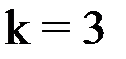

.

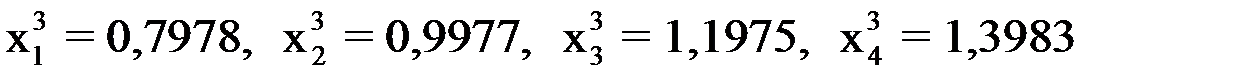при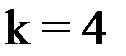

.

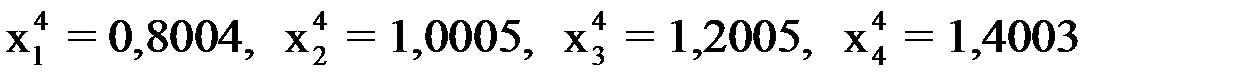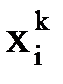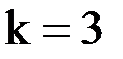Вычисляем модули разностей значений при и :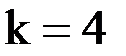

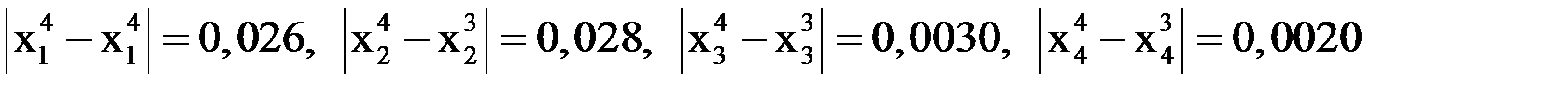. Так как все они больше заданной точности 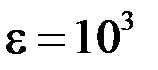, продолжаем итерации.

При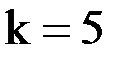

.

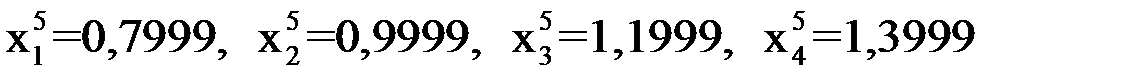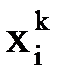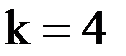Вычисляем модули разностей значений при и :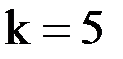

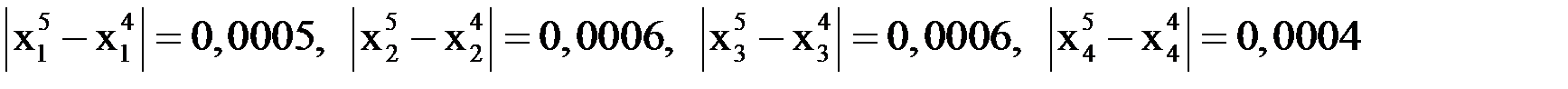. Все они меньше заданной точности 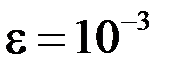, поэтому итерации заканчиваем. Приближенным решением системы являются следующие значения:

.

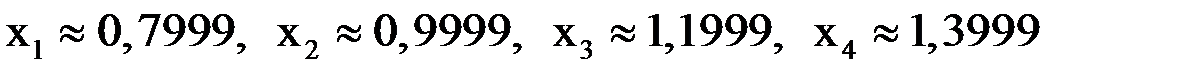Для сравнения приведем точные значения переменных:

.

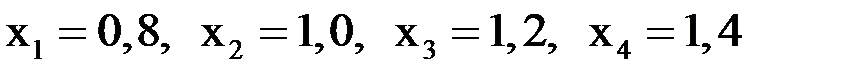Метод Зейделя для решения СЛАУ

Применим метод Зейделя для решения системы уравнений из предыдущего примера. Первые шаги полностью совпадают с процедурой решения по методу простых итераций. Проведем теперь итерации методом Зейделя.

При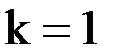

.

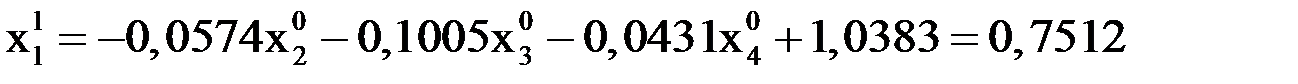При вычислении 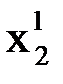используем уже полученное значение :

.

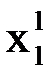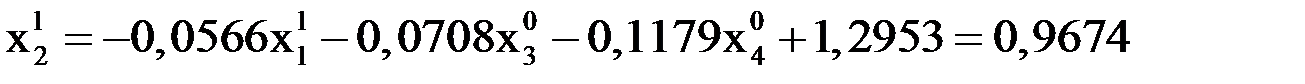При вычислении 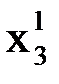используем уже полученные значения и :

.

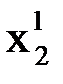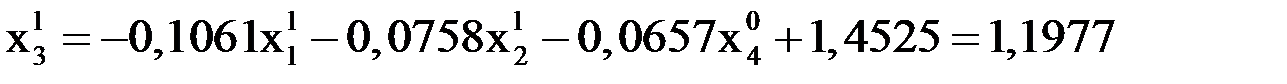При вычислении 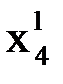используем уже полученные значения , , :

.

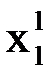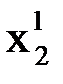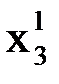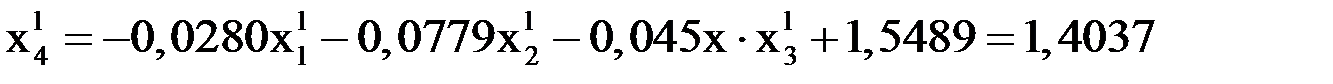Аналогичным образом проведем вычисления пр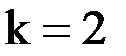и и .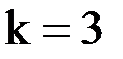

Получим:

при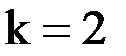

.

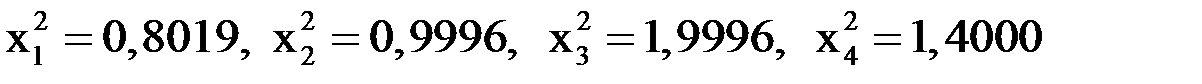при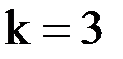

.

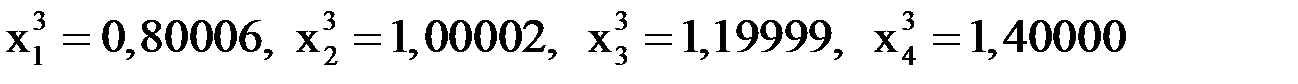Известны точные значения переменных:

.

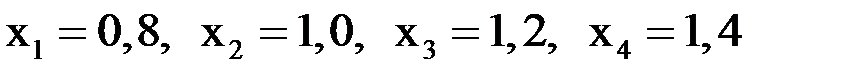Метод Ньютона для решения систем нелинейных уравнений

Методом Ньютона решить систему двух уравнений:

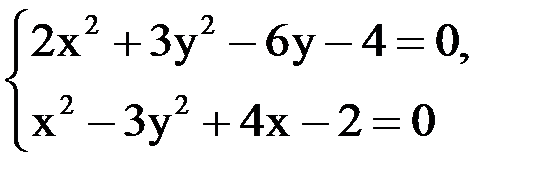с точностью до 0,001.

Решение.

1) Начальные приближения можно определить графическим способом. Для этого перепишем систему в виде: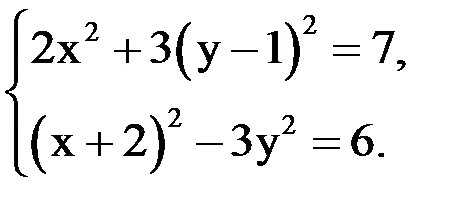

Первое из преобразованных уравнений определяет эллипс, а второе – гиперболу. Данная сис­те­ма имеет два решения. Для уточнения выбирают одно из них, принадлежащее област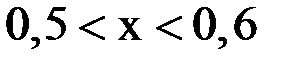и и .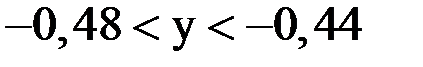

За начальное приближение принимают 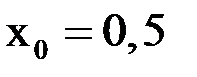и .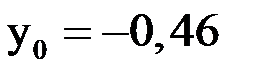

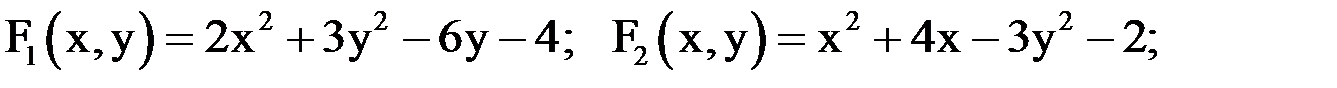
2) Находим

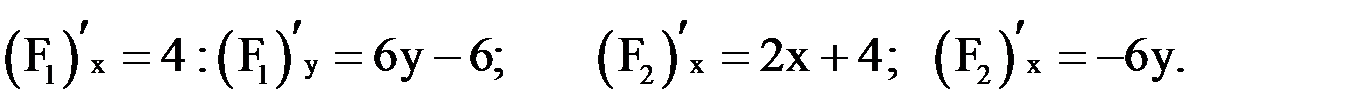
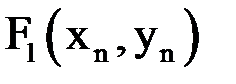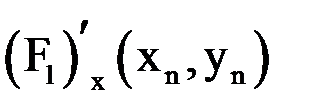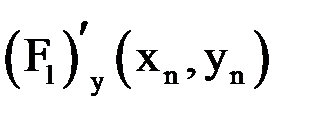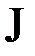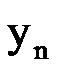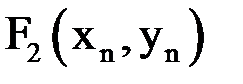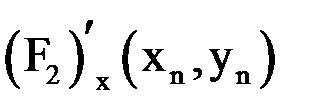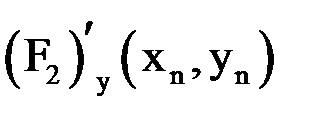0,5	-0,1052		-8,76	49,32
-0,46	-0,3848		2,76
0,5742	0,0114	2,2968	-8,7306	51,2203
-0,4551	0,0052	5,1484	2,7306
0,5727	0,00006	2,2908	-8,7252	51,1375
-0,4542	-0,00011	5,1454	2,7252
0,5727
-0,4542

Поскольку 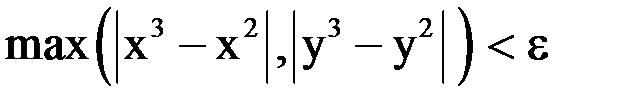, то .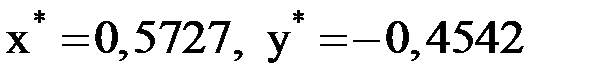

Окончательный ответ: 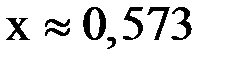и .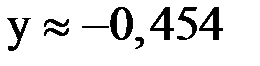

Метод итерации для решения систем нелинейных уравнений

Методом итерации решить систему с точностью до .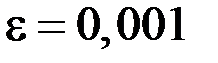

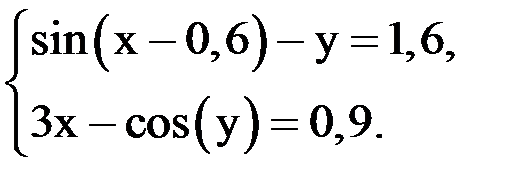
Решение.

1) Приведем систему к форме: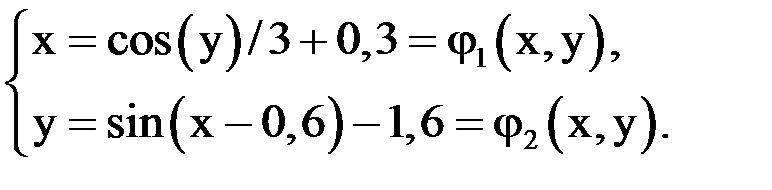

2) Для нахождения начального приближения отделим корни. Построив два графика 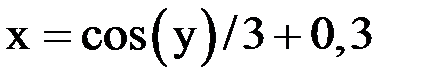и 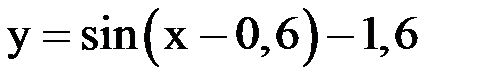и най­дя их точку пересечения, можно увидеть, что система имеет единственное решение, заключенное в об­ласт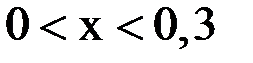и и .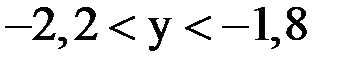

3) Проверим приведенную систему на сходимость итерационного процесса:

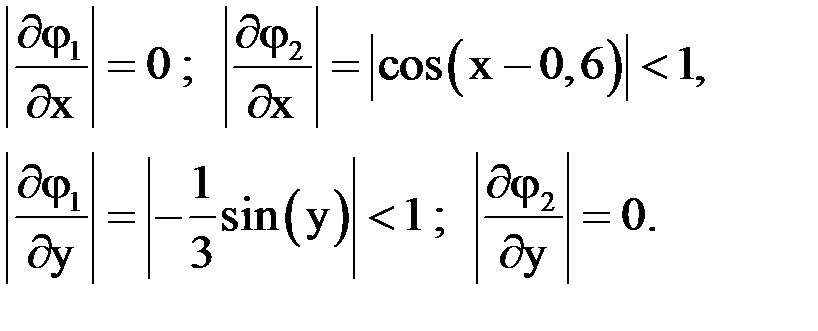
Следовательно,

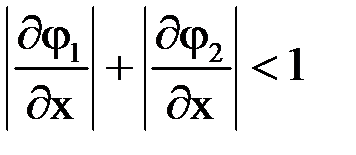и 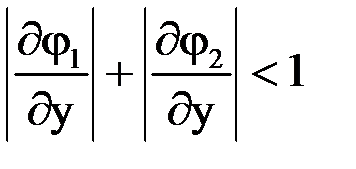т.е. условия сходимости выполняются.

4) Для поиска последовательных приближений используют формулы:

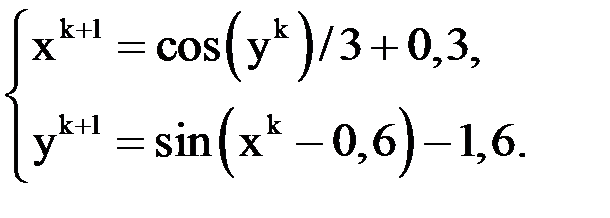
Выберем следующие начальные значения: .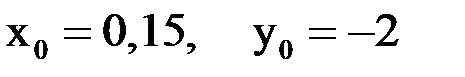

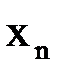	0,15	0,1616	0,1508	0,1539	0,1510	0,1519	0,1510
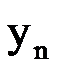	-2	-2,035	-2,0245	-0,0342	-2,0313	-2,0341	-2,0333

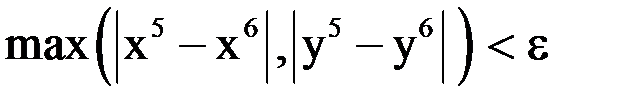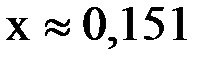Поскольку , то и 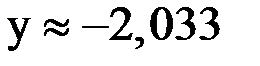.