Остаточный член формулы Тэйлора в интегральной форме и в форме Лагранжа.

Пусть f(x) на 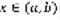имеет непрерывные производные до порядка n+1 включительно, тогда: 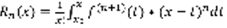(1) , n=0 , 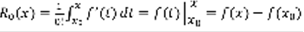, , 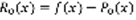, 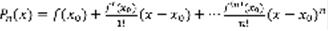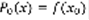. Для n верно, докажем, что верно для n+1: , , , , , .

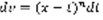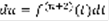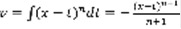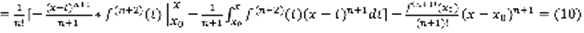Теорема 4: Пусть f(x) для 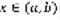имеет первые произвольные до (n+1) порядка включительно, тогда справедлива формула: 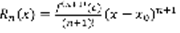(11) – формула Лагранжа остаточного члена, где c- некоторая точка 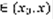. Док-во: 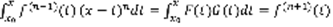=F(t) , 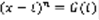, 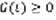. Применим теорему о среднем значении: 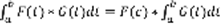. G(t) – знакопостоянна, .

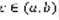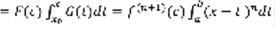
Обыкновенное дифференциальное уравнение, порядок уравнения. Задачи, приводящие к дифференциальным уравнениям (прямолинейное движение точки, движение точки под действием силы тяжести, математический маятник).

Пусть t – независимая переменная, в большинстве случаев имеет значение времени, x(t), x’(t),…,x⁽ⁿ⁾(t) -> ее производные не зависят от t. Дифференциальным уравнением называется уравнение, связывающее все эти величины, то есть уравнение вида: 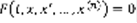(1). Порядок старшей производной, n, называется порядком дифференциального уравнения. Прямолинейное движение материальной точки: рисунок: луч с точкой 0. x(t) – путь, пройденный точкой за время t. Известен закон изменения v движения: v=f(t), требуется найти закон движения самой точки. Рисунок тот же, плюс точки x0, xt. x(t), v=f(t), v=x, x=f(t), 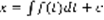, в момент времени 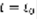точка находится в . Закон движения точки: . 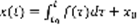Падение материальной точки: m>0, t=0, P=mg, x(0)=x₀, x(0)=v₀. Считаем, что сопротивления нет. 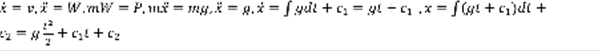, 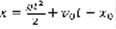. Рисунок: маятник на подвесе, одна линия вниз, другая правее по диагонали, через концы проведена траектория колебаний и из правой линии проведены векторы натяжения, вектор касательной к траектории, перпендикулярный ему, и один перпендикулярный земле. . P=mg, R=-Psinф (ф-угол между векторами, которые вниз направлены). , , , , 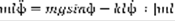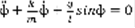k=0 , .

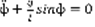Дифференциальное уравнение 1-го порядка, разрешенное относительно производной. Понятия решения и интегральной кривой уравнения. Задача Коши. Теорема существования и единственности решения задачи Коши (теорема Коши). Общее решение. Геометрическая интерпретация дифференциального уравнения 1-го порядка и его решений. Дифференциальное уравнение первого порядка в симметричной форме.

Дифференциальным уравнением первого порядка, разрешенным относительно производной, называется уравнение вида y’=f(x,y) (1). Пусть G – множество точек плоскости. 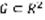– это множество называется областью, если выполняется два требования: 1) 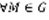входит в G вместе с некоторым кругом с центром в этой точке. 2) любые две точки 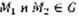можно соединить ломаной, целиком лежащей в G. f(x,y) определена в G-плоскости. Решением уравнения (1) называется всякая функция y=ф(x), которая определена для 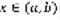, которая обладает следующими свойствами: 1) ф(x) дифференцируема для 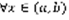, 2) точка 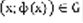для 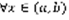. 3) при подстановке y=ф(x) в уравнение (1) получается верное равенство y’(x) = f(x, ф(x)) (2). Задача Коши. Можно показать, что уравнение (1) всегда имеет бесконечно много решений, часто бывает так, что не нужно находить все решения, а нужно найти только решения, которые удовлетворяют определенному условию, это условие называется начальным условием. Выбирается точка 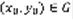и ищется уравнение (1) y(x), которое удовлетворяет условию 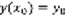(3), называется задачей Коши. Общим решением уравнения (1) в области G называется формула вида (4), где с-произвольная постоянная, обладающая свойствами: 1)при 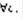(4) – решение (1). 2) 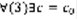. Получающееся из (4) 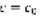удовлетворяет условию (3) ф 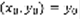. Формула (4)включает в себя решения всех задач Коши. Определение: Пусть y=ф(x) – решение уравнения (1), его график в плоскости x,y называется интегральной кривой уравнения (1). По теореме Коши график должен проходить через точку M₀ в координатах 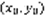. Теорема Коши: Пусть функция f(x,y) непрерывна в области G и имеет непрерывную частную производную 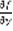, тогда любая задача Коши 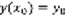имеет единственное решение. Геометрический смысл: в каждой точке проходит одна интегральная кривая. Рассмотрим уравнение: 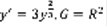, y=o –решение, 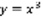- решение. 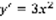, , 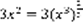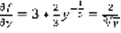- не существует при y=0. Запишем уравнение (1) в ином виде: 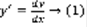, , 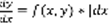f(x,y)dx-dy=0 (5) , M(x,y)dx+N(x,y)dy=(6). (6) называется дифференциальным уравнением 1-го порядка в симметричной форме, т.к. переменные x и y в него входят равноправно. M=f , N=-1. Решением (6) является y=ф(x) , 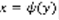при подстановке в (6) даёт верное равенство.