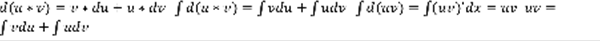Формулы замены переменной и интегрирования по частям в неопределенном интеграле.

Формулы замены переменной и интегрирования по частям в неопределенном интеграле.

Правило замены переменной: Пусть функция x(t) дифференцируема, причем 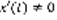, тогда справедливо равенство: 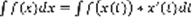(2) Сосчитаем производную по x от левой и правой части равенства (2):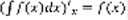 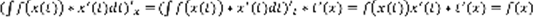. По частям: u=u(x) и v=v(x) –дифференцируемые функции, тогда справедливо равенство: 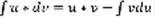Док-во: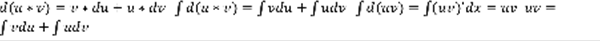

Задача о площади криволинейной трапеции. Определение определенного интеграла и его геометрический смысл.

Рассмотрим на плоскости фигуру, которая ограничена отрезками [a,b] оси ОХ, a<b двумя вертикальными прямыми (уравнениями x=a, x=b). y=f(x), 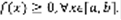Такая фигура называется криволинейной трапецией. Возьмем 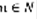и разобьём отрезок [a,b] на n частей. Через точки деления проведем вертикальные отрезки до пересечения с графиком f(x). При этом вся трапеция разобьется на n полосок, площади которых обозначим 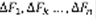. Вся площадь: 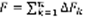. Площадь каждой полосы сосчитаем произвольно, взяв на ее основании произвольную точку . . 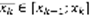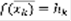Рассмотрим прямоугольник с основанием x_k-1,x_k и высотой h_k. Длина основания: 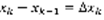, тогда площадь прямоугольника: 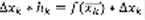. . 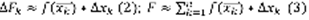Точность приближенного равенства (3) тем выше, чем мельче дробление [a,b] на части. Рангом дробления отрезка [a,b] называется максимальная из длин его частей дробления, обозначается 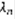. . 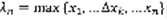Если 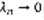, то в пределе приближенное равенство (3) превратится в точное: . Определение. Если предел (4) существует и не зависит ни от способа разбиения промежутка на части, ни от выбора точек в каждой части разбиения, то он называется определенным интегралом от функции f(x) по промежутку [a,b] и обозначается как 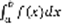. 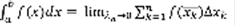(3). Геометрический смысл: сравнивая (3) и (4), получаем, что если a<b, а функци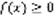я для 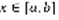, то интеграл от a до b равен площади трапеции. Теорема: Если функция f(x) непрерывна для 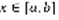, то тогда f(x) интегрируема на [a,b].

Основные свойства определенного интеграла.

1-е свойство: при перемене местами пределов интегрирования интеграл поменяет знак. Док-во: предположим, что 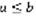, , 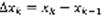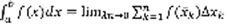(2), 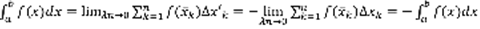, т.к. 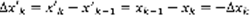. Тут рисунок, там две параллельные числовые прямые, на верхней точки a, 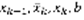, на нижней прям под этими точками 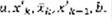Следствие: если в интеграле нижний предел совпадает с верхним, то интеграл = 0. , 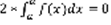. 2-е свойство: линейность интеграла. Пусть имеется две функции: f(x) и g(x), интегрируемые на [a,b], тогда A*f(x)+B*g(x) интегрированы на [a,b]. Док-во: 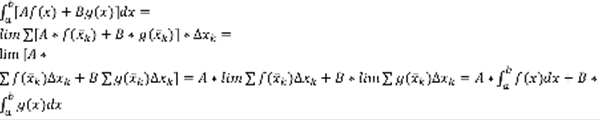, ч.т.д. 3-е свойство: аддитивность интеграла. При любом расположении точек a,b,c выполняется равенство: 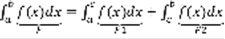(3). Геометрическое док-во: 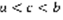, 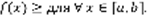F=F1+F2. Там рисунок числовая ось, кривая, на ее концах пунктиры вниз на ось х, в точки a,b,c. 4-е свойство: интегрирование неравенств: 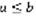. Пусть для 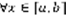выполняется неравенство: 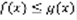, тогда: 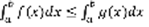(4) Док-во: рассмотрим разность 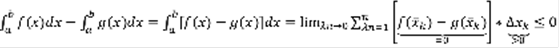, следовательно (4). Следствия: 1) Пусть 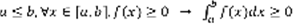(5) 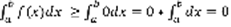2) Пусть 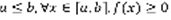, пусть функция f(x) непрерывна на [a,b], пусть существует точка 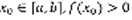, тогда 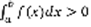(6) рисунок: оси xy, на х точки а, с1, х0, с2, b, кривая от точки а до б.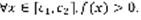 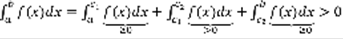, ч.т.д. 5-е свойство: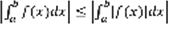

Формула Ньютона-Лейбница.

Теорема: Пусть f(x) непрерывна для 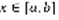, пусть F(x) – какая-нибудь ее первообразная, тогда 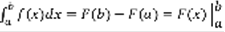(1) Док-во: Рассмотрим 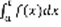. По теореме Барроу: 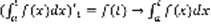–первообразная для f(t), по условию F(t) тоже первообразная для f(t), отсюда: 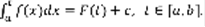Если t=a, то 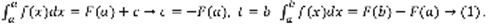, ч.т.д.

Обыкновенное дифференциальное уравнение, порядок уравнения. Задачи, приводящие к дифференциальным уравнениям (прямолинейное движение точки, движение точки под действием силы тяжести, математический маятник).

Пусть t – независимая переменная, в большинстве случаев имеет значение времени, x(t), x’(t),…,x⁽ⁿ⁾(t) -> ее производные не зависят от t. Дифференциальным уравнением называется уравнение, связывающее все эти величины, то есть уравнение вида: 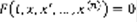(1). Порядок старшей производной, n, называется порядком дифференциального уравнения. Прямолинейное движение материальной точки: рисунок: луч с точкой 0. x(t) – путь, пройденный точкой за время t. Известен закон изменения v движения: v=f(t), требуется найти закон движения самой точки. Рисунок тот же, плюс точки x0, xt. x(t), v=f(t), v=x, x=f(t), 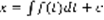, в момент времени 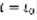точка находится в . Закон движения точки: . Падение материальной точки: m>0, t=0, P=mg, x(0)=x₀, x(0)=v₀. Считаем, что сопротивления нет. 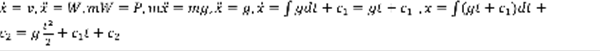, 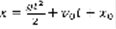. Рисунок: маятник на подвесе, одна линия вниз, другая правее по диагонали, через концы проведена траектория колебаний и из правой линии проведены векторы натяжения, вектор касательной к траектории, перпендикулярный ему, и один перпендикулярный земле. . P=mg, R=-Psinф (ф-угол между векторами, которые вниз направлены). , , , , 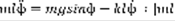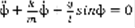k=0 , .

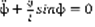Дифференциальное уравнение 1-го порядка, разрешенное относительно производной. Понятия решения и интегральной кривой уравнения. Задача Коши. Теорема существования и единственности решения задачи Коши (теорема Коши). Общее решение. Геометрическая интерпретация дифференциального уравнения 1-го порядка и его решений. Дифференциальное уравнение первого порядка в симметричной форме.

Дифференциальным уравнением первого порядка, разрешенным относительно производной, называется уравнение вида y’=f(x,y) (1). Пусть G – множество точек плоскости. 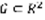– это множество называется областью, если выполняется два требования: 1) 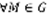входит в G вместе с некоторым кругом с центром в этой точке. 2) любые две точки 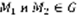можно соединить ломаной, целиком лежащей в G. f(x,y) определена в G-плоскости. Решением уравнения (1) называется всякая функция y=ф(x), которая определена для 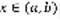, которая обладает следующими свойствами: 1) ф(x) дифференцируема для 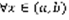, 2) точка 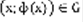для 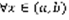. 3) при подстановке y=ф(x) в уравнение (1) получается верное равенство y’(x) = f(x, ф(x)) (2). Задача Коши. Можно показать, что уравнение (1) всегда имеет бесконечно много решений, часто бывает так, что не нужно находить все решения, а нужно найти только решения, которые удовлетворяют определенному условию, это условие называется начальным условием. Выбирается точка 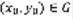и ищется уравнение (1) y(x), которое удовлетворяет условию 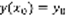(3), называется задачей Коши. Общим решением уравнения (1) в области G называется формула вида (4), где с-произвольная постоянная, обладающая свойствами: 1)при 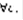(4) – решение (1). 2) 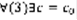. Получающееся из (4) 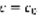удовлетворяет условию (3) ф 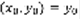. Формула (4)включает в себя решения всех задач Коши. Определение: Пусть y=ф(x) – решение уравнения (1), его график в плоскости x,y называется интегральной кривой уравнения (1). По теореме Коши график должен проходить через точку M₀ в координатах 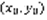. Теорема Коши: Пусть функция f(x,y) непрерывна в области G и имеет непрерывную частную производную 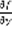, тогда любая задача Коши 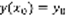имеет единственное решение. Геометрический смысл: в каждой точке проходит одна интегральная кривая. Рассмотрим уравнение: 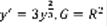, y=o –решение, 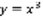- решение. 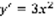, , 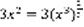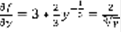- не существует при y=0. Запишем уравнение (1) в ином виде: 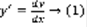, , 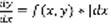f(x,y)dx-dy=0 (5) , M(x,y)dx+N(x,y)dy=(6). (6) называется дифференциальным уравнением 1-го порядка в симметричной форме, т.к. переменные x и y в него входят равноправно. M=f , N=-1. Решением (6) является y=ф(x) , 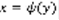при подстановке в (6) даёт верное равенство.

Комплексные числа. Изображение комплексных чисел. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа. Действия с комплексными числами. Возведение в степень комплексных чисел.

Пусть a и b – вещественные числа 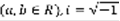. Комплексным числом называется число вида 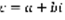(1). a=Real c, b=Imaginary c. Определение: Пусть 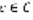, C-множество комплексных чисел. Модулем комплексного числа называется число вида: 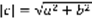. ф=argc 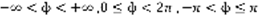. 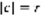, , 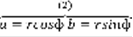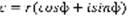(3). Определение: 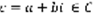, сопряженным к нему является число вида 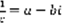. 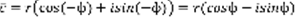, 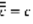. Операции над комплексными числами: 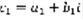, 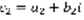. 1) Сложение: 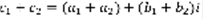. 2) Разность: 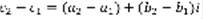. 3) Умножение: 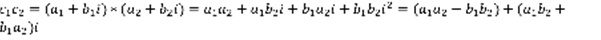. 4) Деление: . Если комплексные числа заданы в тригонометрической форме, то 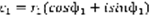, 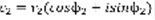. Умножение: 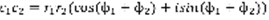. Деление: 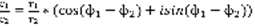. Пусть , n-ой степенью с называется его произведение само на себя n раз. 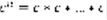. c=a+bi , 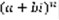. 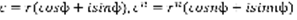, формула Муавра: .

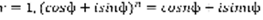26. Нахождение линейно независимых частных решений линейного однородного уравнения 2-го порядка с постоянными коэффициентами (метод Эйлера).

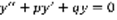(1). p,q – постоянные. 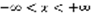. Лемма: Для того, чтобы уравнение (1) имело решение вида 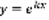(2), где k – постоянная, необходимо и достаточно, чтобы k было корнем квадратного уравнения. 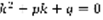(3). Доказательство: 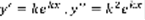, 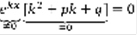. (3) называется характеристическим уравнением для дифференциального уравнения (2) и играет основную роль в нахождении ФСР. 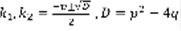. 1) D>0 , 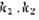– веществ. 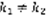, 2)D=0 , 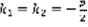–вещественный корень . 3) D<0 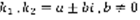. Теорема о видах ФСР: 1)Если D>0, то ФСР имеет вид 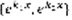, 2)Если D=0, то ФСР имеет вид 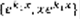, 3)Если D<0, ФСР 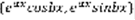. Доказательство: 1)на основании Леммы. 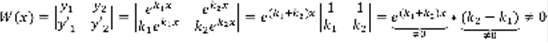– решение линейно независимо. 2) 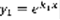– решение по лемме. 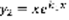– решение (1) , 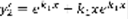, 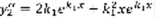. 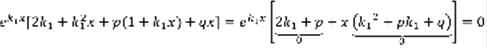, 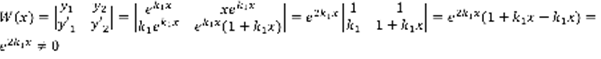–линейно независимо. 3) 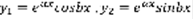. 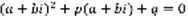, 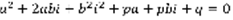–комплексное число, 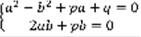(4), 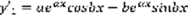, , 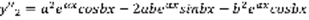, , 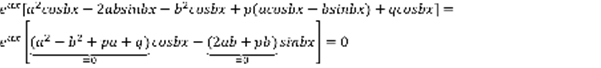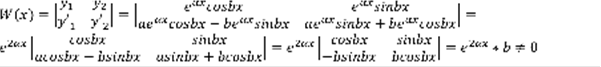– линейно независимо.

ЧИСЛОВЫЕ РЯДЫ

1. Понятия числового ряда, его общего члена, частичных сумм и суммы (в случае его сходимости). Геометрическая прогрессия.

Пусть имеется бесконечная числовая последовательность 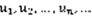Определение: бесконечным числовым рядом называется следующая формальная сумма: 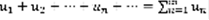(1) 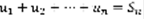– n-я частичная сумма (1). 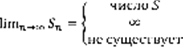(2). Определение: 1)Если предел (2) существует и конечен, то ряд (1) называется сходящимся, при этом S называется суммой ряда. 2)В противном случае ряд (1) называется расходящимся и говорят, что он суммы не имеет. Геометрическая прогрессия – числовая последовательность, каждый член которой, начиная со 2-го равен предыдущему, умноженному на некоторое постоянное для этой прогрессии число, которое называется знаменателем прогрессии.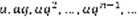 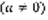, 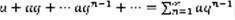(3) 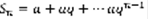. 1)q=1 , 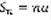, 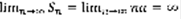- расходится. 2) , , .

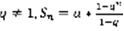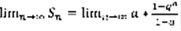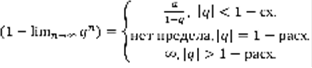Формулы замены переменной и интегрирования по частям в неопределенном интеграле.

Правило замены переменной: Пусть функция x(t) дифференцируема, причем 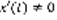, тогда справедливо равенство: 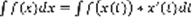(2) Сосчитаем производную по x от левой и правой части равенства (2):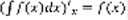 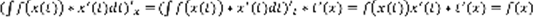. По частям: u=u(x) и v=v(x) –дифференцируемые функции, тогда справедливо равенство: 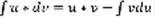Док-во: