Интерполяция кубическими сплайнами

Интерполяция кубическими сплайнами состоит в сглаживании кривой так, что первая и вторая производные сглаживаемой кривой являются непрерывными. Искомая кривая определяется рядом соединенных отрезков кубических функций. Интерполяция осуществляется в 3 этапа:

1. Исходные данные требуется представить в виде матрицы, где каждый из двух столбцов - это вектор значений D_i и H_i. Затем, используя функцию V=csort(M,N),отсортировать значения матрицы по столбцу Di в порядке возрастания. В данном формате функции csort(M,N) M– обозначение матрицы, N– номер столбца, по которому производится сортировка.

1. 
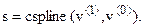
   Использование функции s=cspline(x,y) на векторах x и y возвращает вектор s, содержащий значения вторых производных сглаживаемой кривой в заданных точках. В качестве векторов x и yследует задатьзначения D_i и H_i, что соответствует столбцам V<0>и V<1>:

1. Использование функции interpпозволяет найти значения функции q(z) для промежуточных значений zиз интервала от Dmin до Dmax:

q(z)=interp(s,x,y,z)

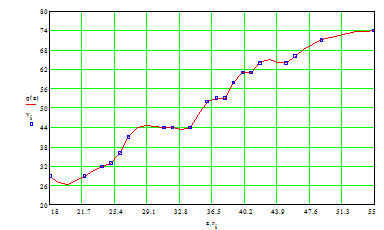
Рис. 3.1

В результате интерполяции кубическими сплайнами должен быть представлен интерполяционный график, состоящий из точечного графика исходных значений диаметра и высоты дерева и гладкой интерполяционной кривой, проходящей через данные точки.

Приближение функции с использованием метода наименьших квадратов

Определение коэффициентов линейной регрессии с помощью решающего блока

a := 1 b := 1 - Задание начальных значений переменных

Given- Ключевое слово, указывающее на начало блока

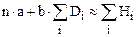
- Совокупность решаемых уравнений

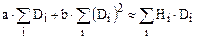
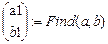
- Функция Find находит искомые значения

коэффициентов в уравнениях.

После нахождения коэффициентов линейного уравнения записывается уравнение связи и строится график корреляционной зависимости

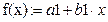
- Уравнение связи

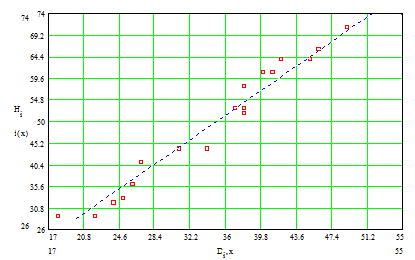
Рис. 3.2

3.4. Решить данную задачу линейной интерполяции с помощью встроенной функции line(vx,vy)

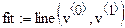
Встроенная функция line(vx,vy) по методу наименьших квадратов находит коэффициенты a и b в линейном уравнении регрессии y(x)=ax+b

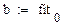
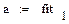
Найти коэффициент корреляции, используя встроенную функцию corr(vx,vy).

3.5. Решить данную задачу методом кубической интерполяции

Уравнение связи двух величин D и H:

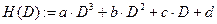
Используя метод наименьших квадратов можно получить систему уравнений для вычисления параметров a,b,c,d.

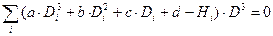
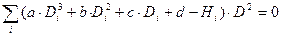
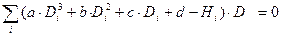
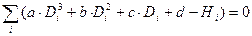
Построить график кубической функции

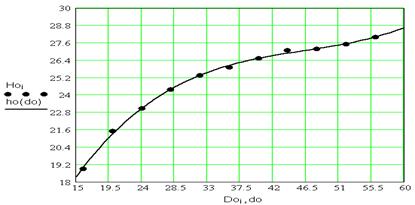
3.6. Выводы по работе

Рис. 3.3

Лабораторная работа 4

Решение задачи Коши для обыкновенного дифференциального уравнения

Цель работы:

Знакомство и анализ наиболее распространенных численных методов решения дифференциальных уравнений первого порядка.

Время выполнения работы 4 часа.

4.1. Индивидуальное задание