Методические указания для заочников
Министерство сельского хозяйства Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Казанский государственный аграрный университет
Кафедра физики и математики
МАТЕМАТИКА
Методические указания для заочников
К выполнению контрольной работы
Казань 2017
ТЕМА 6. Интегральное исчисление функции одной Переменной
Неопределенный интеграл. Основные понятия
Определение. Неопределенным интегралом от функции 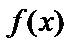 называется выражение вида
называется выражение вида 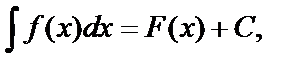 если
если 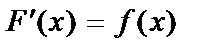 . Функция
. Функция 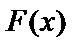 называется первообразной для заданной функции
называется первообразной для заданной функции 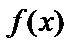 .
.
Например, если 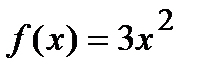 , то
, то 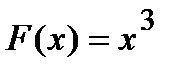 .
.
Свойства неопределенного интеграла
1) 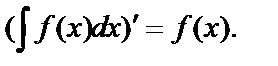
2) 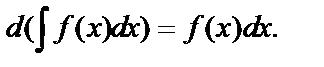
3) 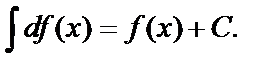
4) 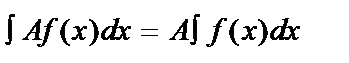 , где A ≠ 0.
, где A ≠ 0.
5) 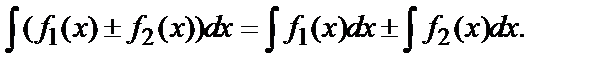
Таблица основных неопределенных интегралов
1. 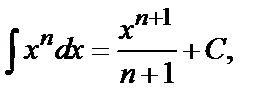 где
где 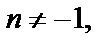 (
( 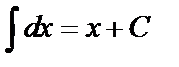 ).
).
2. 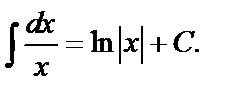
3. 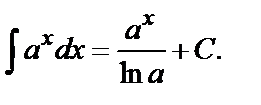
4. 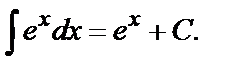
5. 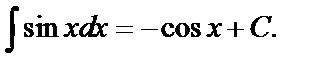
6. 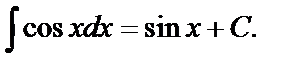
7. 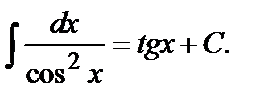
8. 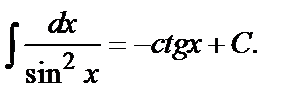
9. 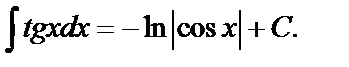
10. 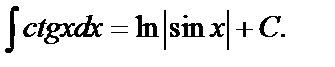
11. 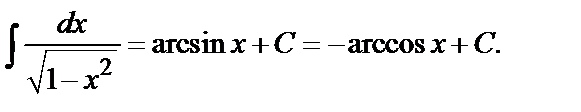
12. 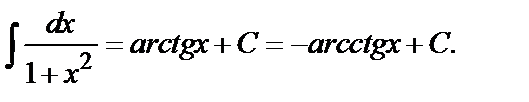
13. 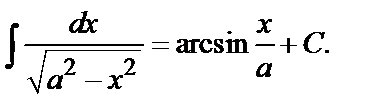
14. 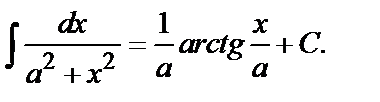
15. 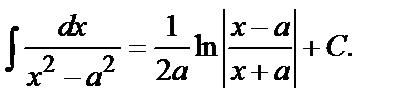
16. 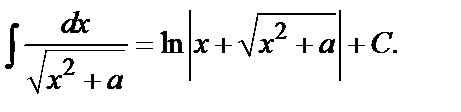
Методы интегрирования
При интегрировании наиболее часто используются следующие методы.
1) Если 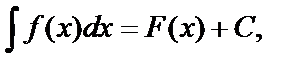 то
то
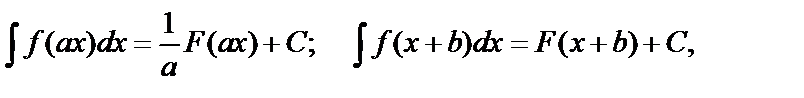 (1)
(1)
где а и b–некоторые постоянные.
2) Подведение под знак дифференциала:
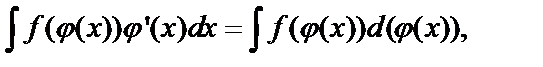 (2)
(2)
так как 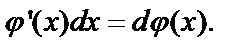
3) Формула интегрирования по частям:
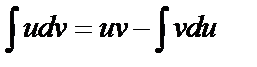 (3)
(3)
Обычно выражение 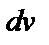 выбирается так, чтобы его интегрирование не вызывало особых затруднений. За
выбирается так, чтобы его интегрирование не вызывало особых затруднений. За 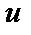 , как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида
, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида 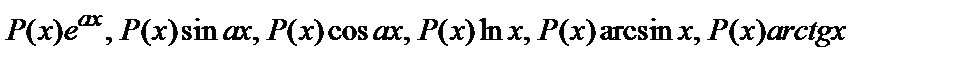 , где
, где 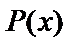 –многочлен от х.
–многочлен от х.
4) Интегрирование рациональных дробей, т.е. отношений двух многочленов 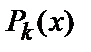 и
и 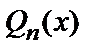 (соответственно
(соответственно 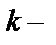 й и n
й и n 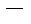 й степени):
й степени): 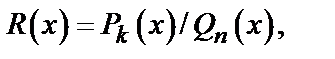 сводится к разложению подынтегральной функции
сводится к разложению подынтегральной функции 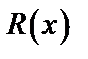 на элементарные, всегда интегрируемые дроби вида:
на элементарные, всегда интегрируемые дроби вида:
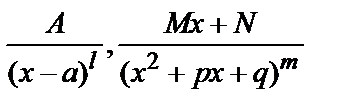 , (4)
, (4)
где l и m –целые положительные числа, а трехчлен 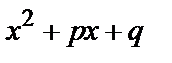 не имеет действительных корней. При этом в случае неправильной дроби (
не имеет действительных корней. При этом в случае неправильной дроби ( 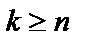 ) должна быть предварительно выделена целая часть.
) должна быть предварительно выделена целая часть.
5) Интегрирование методом замены переменной (способом подстановки) является одним из эффективных приемов интегрирования. Его сущность состоит в переходе от переменной х к новой переменой t: 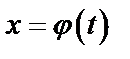 . Наиболее целесообразная для данного интеграла замена переменной, т.е. выбор функции
. Наиболее целесообразная для данного интеграла замена переменной, т.е. выбор функции 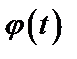 , не всегда очевидна. Однако для некоторых часто встречающихся классов функций можно указать такие стандартные подстановки:
, не всегда очевидна. Однако для некоторых часто встречающихся классов функций можно указать такие стандартные подстановки:
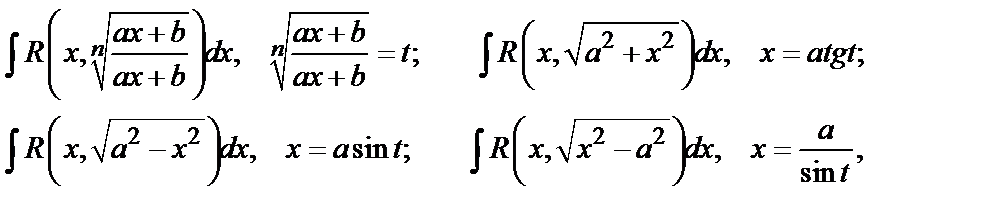
где R– символ рациональной функции.
6.5. Формула Ньютона-Лейбница для вычисления определенного интеграла имеет вид:
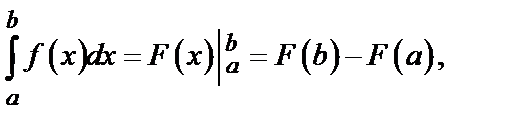 (5)
(5)
если 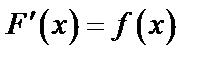 и первообразная
и первообразная 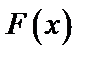 непрерывна на отрезке
непрерывна на отрезке 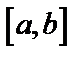 .
.
Определенный интеграл численно равен площади криволинейной трапеции, ограниченной прямыми
x = a, x = b, y = 0 и частью графика функции 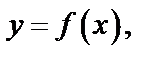 взятой со знаком плюс, если
взятой со знаком плюс, если 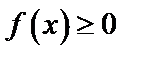 , и со знаком минус, если
, и со знаком минус, если 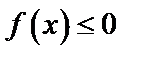 .
.
6.6. Решение типового задания
Пример 1. Найти 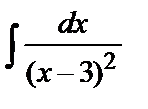 .
.
Решение. Так как 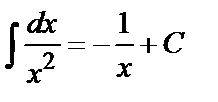 то, используя формулы (1), получим
то, используя формулы (1), получим
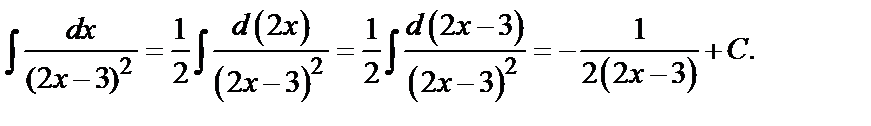
Проверка:
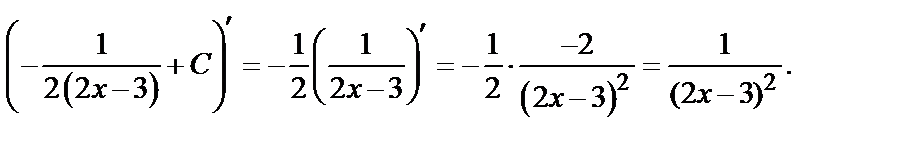
Пример 2. Найти 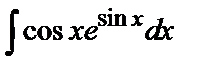 .
.
Решение. Так как 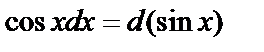 , то по формуле (2) находим
, то по формуле (2) находим
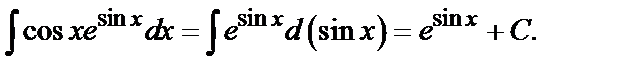
Пример 3. Найти 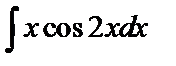 .
.
Решение. Применим метод интегрирования по частям. Положим 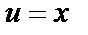 ,
, 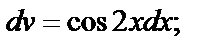 тогда
тогда 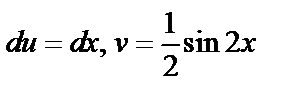 . Используя формулу (3), имеем
. Используя формулу (3), имеем
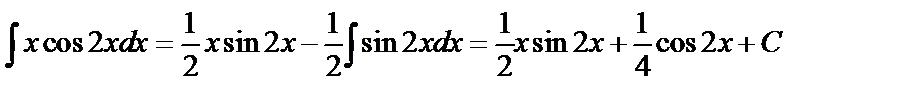 .
.
Пример 4. Найти 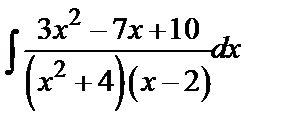 .
.
Решение. Подынтегральная рациональная дробь является правильной и разлагается на элементарные дроби вида (4):
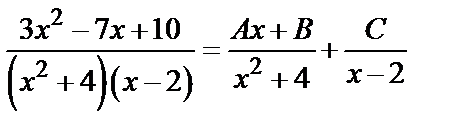 .
.
Освобождаясь от знаменателей в обеих частях этого равенства и приравнивая числители, получаем тождество для вычисления неопределенных коэффициентов 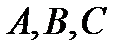 :
:
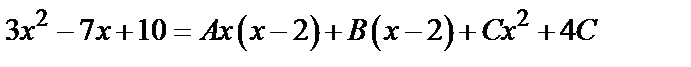 .
.
Составим систему трех уравнений с тремя неизвестными. Одно уравнение получим, полагая х=2 (корень знаменателя подынтегральной функции). Два других получим, приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, например 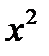 и
и 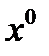 при:
при:
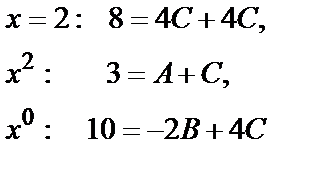
Решение этой системы дает: 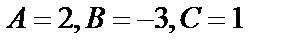 . Таким образом,
. Таким образом,
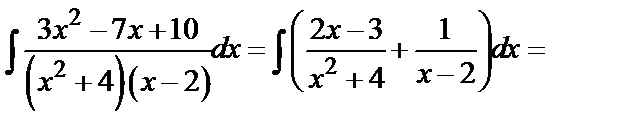

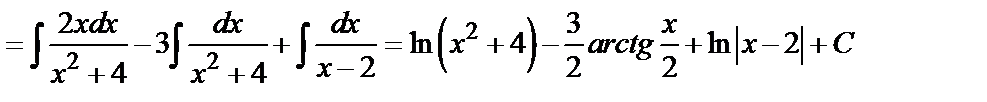 .
.
Пример 5. Вычислить определенный интеграл 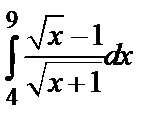 .
.
Решение. Применим метод замены переменной; положим 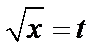 , откуда
, откуда 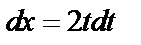 . Найдем пределы интегрирования по переменой t: при
. Найдем пределы интегрирования по переменой t: при 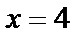 имеем
имеем 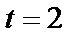 , а при
, а при 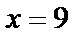 имеем
имеем 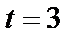 . Переходя в исходном интеграле к новой переменной
. Переходя в исходном интеграле к новой переменной 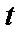 и применяя формулу Ньютона-Лейбница (5), получаем:
и применяя формулу Ньютона-Лейбница (5), получаем:
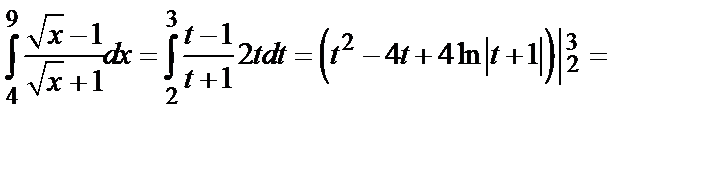
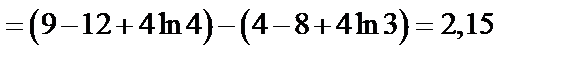 .
.
Задачи 181-210:
Вычислите неопределенные интегралы:
181. а) 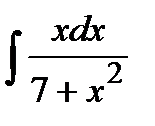 | б) 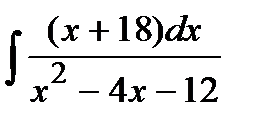 | в) 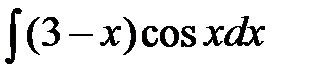 |
182. а) 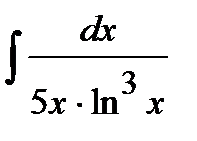 | б) 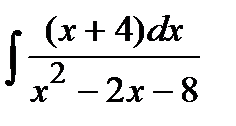 | в) 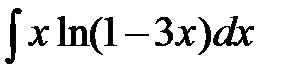 |
183. а) 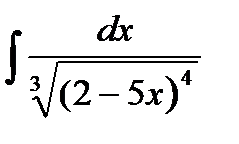 | б) 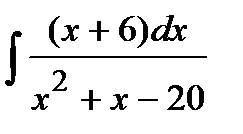 | в) 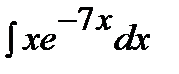 |
184. а) 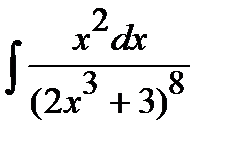 | б) 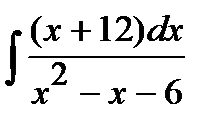 | в) 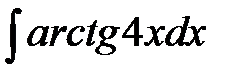 |
185. а) 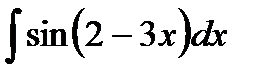 | б) 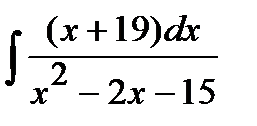 | в) 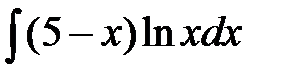 |
186. а) 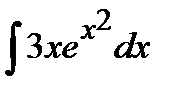 | б) 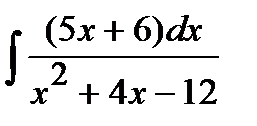 | в)  |
187. а) 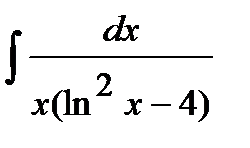 | б) 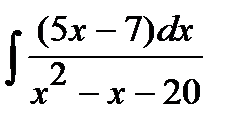 | в) 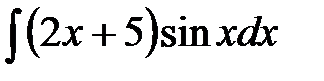 |
188. а) 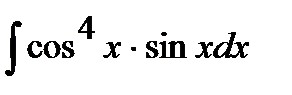 | б) 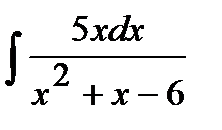 | в) 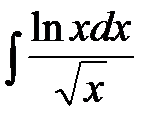 |
189. а) 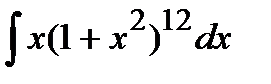 | б) 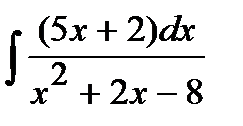 | в) 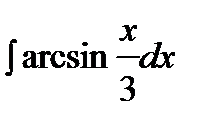 |
190. а) 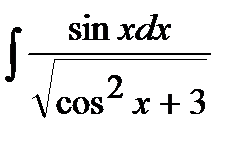 | б) 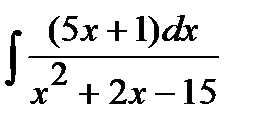 | в) 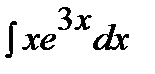 |
191. а) 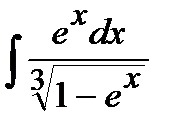 | б) 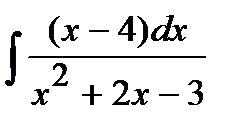 | в) 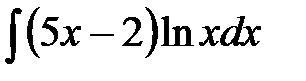 |
192. а)  | б) 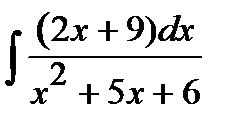 | в) 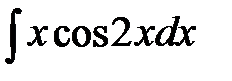 |
193. а) 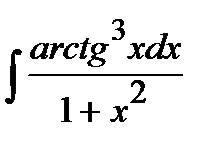 | б) 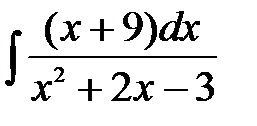 | в) 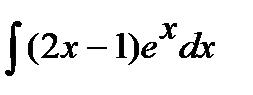 |
194. а) 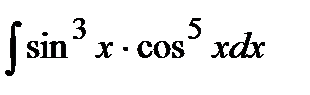 | б) 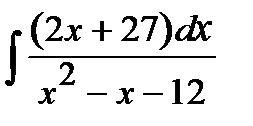 | в) 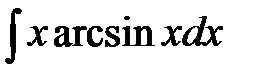 |
195. а) 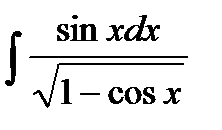 | б) 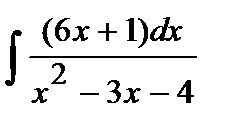 | в) 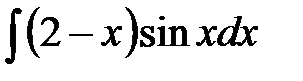 |
196. а) 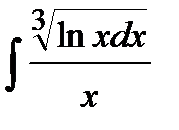 | б) 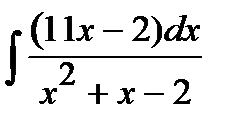 | в) 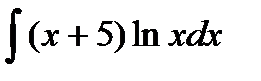 |
197. а) 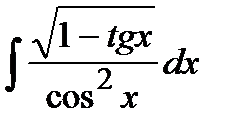 | б) 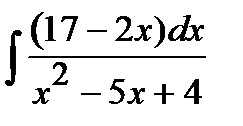 | в) 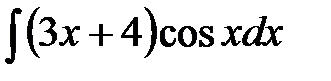 |
198. а) 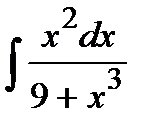 | б) 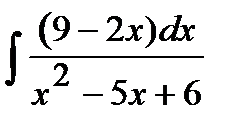 | в) 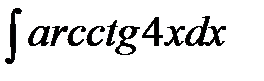 |
199. а) 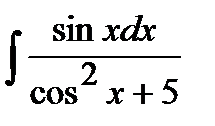 | б) 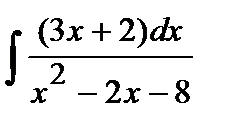 | в) 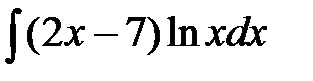 |
200. а) 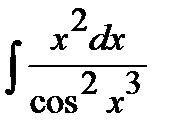 | б) 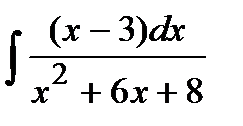 | в) 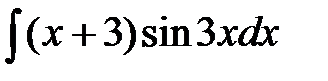 |
201. a) 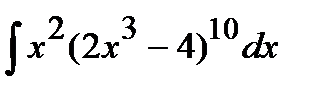 | б) 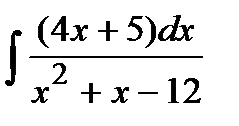 | в) 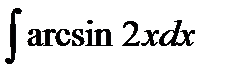 |
202. a) 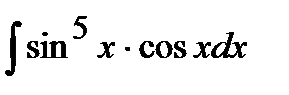 | б) 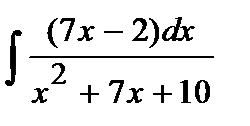 | в) 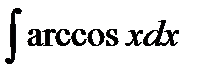 |
203. a) 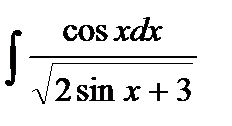 | б) 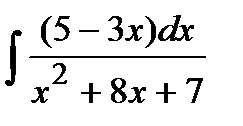 | в) 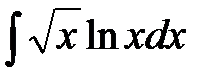 |
204. a) 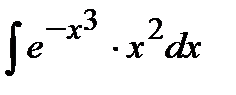 | б) 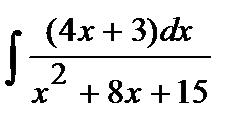 | в) 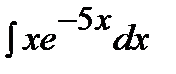 |
205. a) 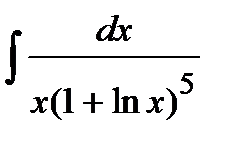 | б) 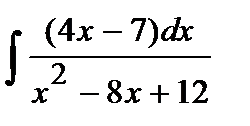 | в) 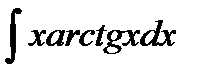 |
206. a) 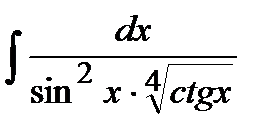 | б) 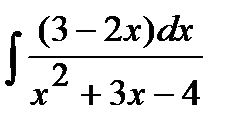 | в) 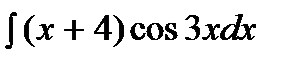 |
207. a) 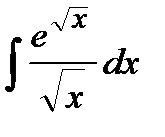 | б) 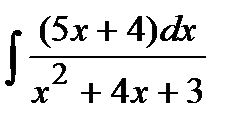 | в) 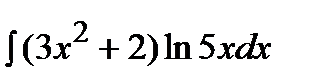 |
208. a) 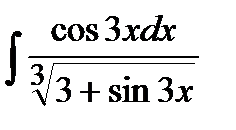 | б) 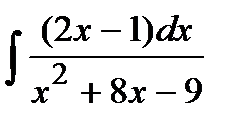 | в) 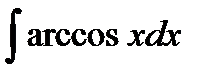 |
209. a) 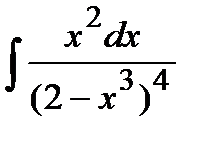 | б) 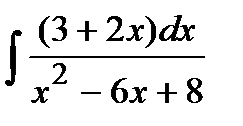 | в) 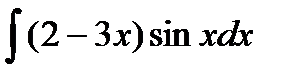 |
210. a) 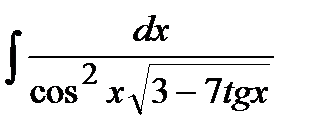 | б) 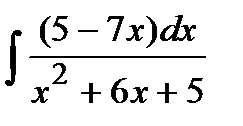 | в) 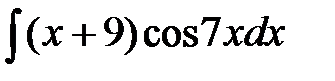 |
Задачи 211-240:
Вычислить площадь фигуры, ограниченной данными линиями: Сделать чертеж и заштриховать искомую площадь.
211. 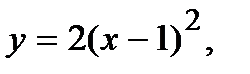 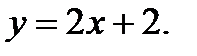 | 226. 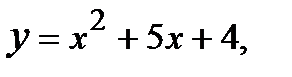 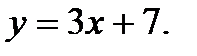 |
212. 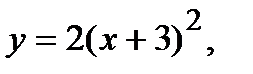 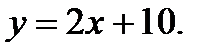 | 227. 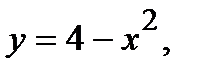 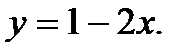 |
213. 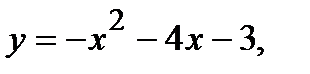 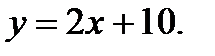 | 228. 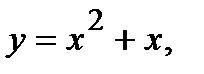 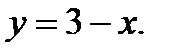 |
214. 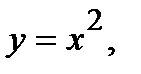 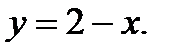 | 229. 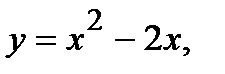 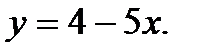 |
215. 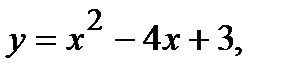 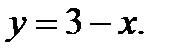 | 230. 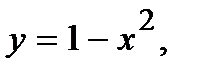 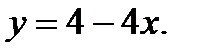 |
216. 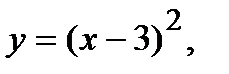 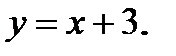 | 231. 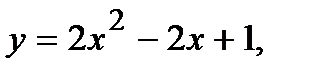 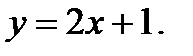 |
217. 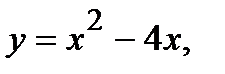 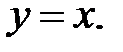 | 232. 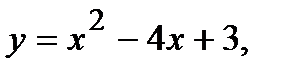 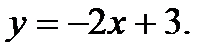 |
218. 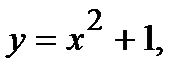 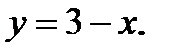 | 233. 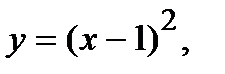 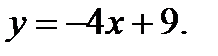 |
219. 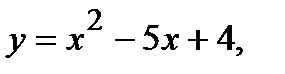 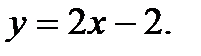 | 234. 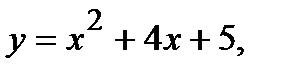 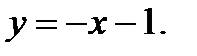 |
220. 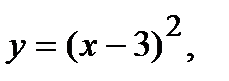 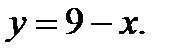 | 235. 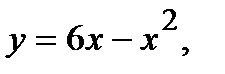 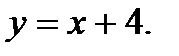 |
211. 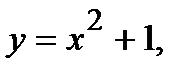 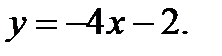 | 236. 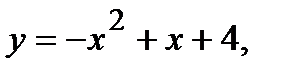 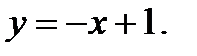 |
222. 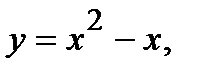 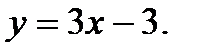 | 237. 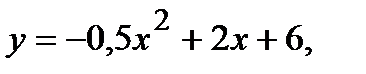 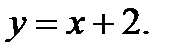 |
223. 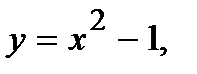 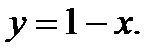 | 238. 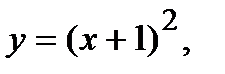 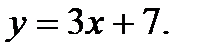 |
224. 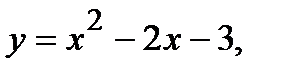 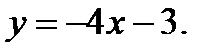 | 239. 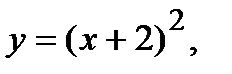 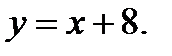 |
225. 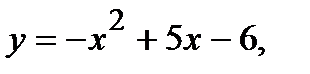 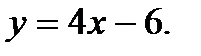 | 240. 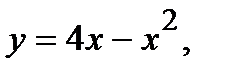 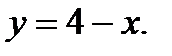 |
Функция нескольких переменных. Основные понятия
Определение. Пусть даны два непустых множества D и U. Если каждой паре действительных чисел (x; y), принадлежащей множеству D, по определенному правилу ставится в соответствии один и только один элемент u из U, то говорят, что на множестве D задана функция f (или отображение) со множеством значений U. При этом пишут  , или
, или  , или
, или  . Множество D называется областью определения функции, а множество U, состоящее из всех чисел вида
. Множество D называется областью определения функции, а множество U, состоящее из всех чисел вида  , где
, где  ,
,  множеством значений функции. Значение функции
множеством значений функции. Значение функции  в точке
в точке  называется частным значением функции и обозначается
называется частным значением функции и обозначается  или
или  .
.
Полный дифференциал
Полным приращением функции  в точке
в точке  называется разность
называется разность  где
где  и
и 
 произвольные приращения аргументов.
произвольные приращения аргументов.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если в этой точке полное приращение можно представить в виде
, если в этой точке полное приращение можно представить в виде
 , где
, где  .
.
Полным дифференциалом функции  называется главная часть полного приращения
называется главная часть полного приращения  , линейная относительно приращений аргументов
, линейная относительно приращений аргументов  и
и  , т.е.
, т.е.  .
.
Дифференциалы независимых переменных совпадают с их приращениями, т.е.  и
и  .
.
Полный дифференциал функции  вычисляется по формуле
вычисляется по формуле
 .
.
Аналогично, полный дифференциал функции трех аргументов  вычисляется по формуле
вычисляется по формуле
 .
.
При достаточно малом  для дифференцируемой функции
для дифференцируемой функции  справедливы приближенные равенства
справедливы приближенные равенства
 .
.
Экстремум функции
Функция 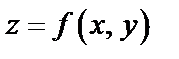 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 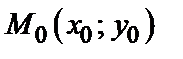 , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке
, если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке 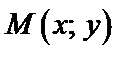 некоторой окрестности точки
некоторой окрестности точки 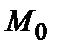 , т.е.
, т.е. 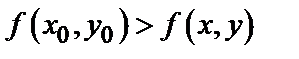 [соответственно
[соответственно 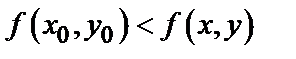 ] для всех точек
] для всех точек 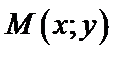 , удовлетворяющих условию
, удовлетворяющих условию 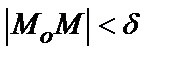 , где
, где 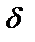
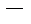 достаточно малое положительное число.
достаточно малое положительное число.
Максимум или минимум функции называется ее экстремумом. Точка 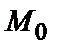 , в которой функция имеет экстремум, называется точкой экстремума.
, в которой функция имеет экстремум, называется точкой экстремума.
Если дифференцируемая функция 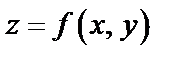 достигает экстремума в точке
достигает экстремума в точке 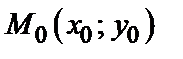 , то ее частные производные первого порядка в этой точке равны нулю, т.е.
, то ее частные производные первого порядка в этой точке равны нулю, т.е.
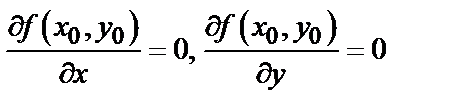
(необходимые условия экстремума).
Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.
Пусть 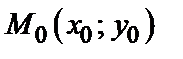
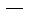 стационарная точка функции
стационарная точка функции 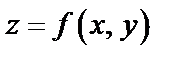 . Обозначим
. Обозначим
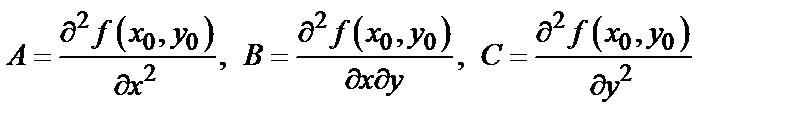
и составим дискриминант 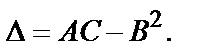 Тогда:
Тогда:
а) если 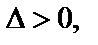 то функция имеет в точке
то функция имеет в точке 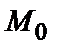 экстремум, а именно максимум при
экстремум, а именно максимум при 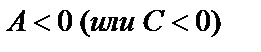 и минимум при
и минимум при 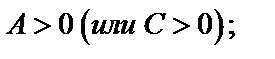
б) если 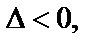 то в точке
то в точке 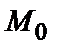 экстремума нет (достаточные условия наличия или отсутствия экстремума);
экстремума нет (достаточные условия наличия или отсутствия экстремума);
в) если 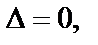 то требуется дальнейшее исследование (сомнительный случай).
то требуется дальнейшее исследование (сомнительный случай).
7.7. Решение типового задания
Пример 1.Дана функция 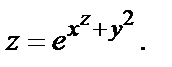 Найти
Найти 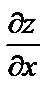 и
и 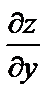 .
.
Решение.
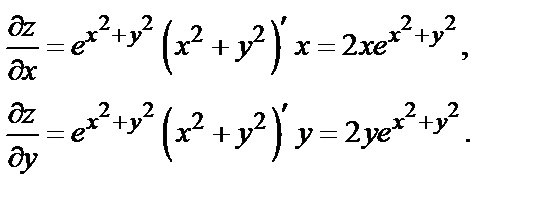
Пример 2. Дана функция 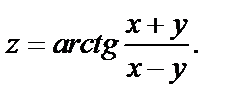 Найти dz.
Найти dz.
Решение.
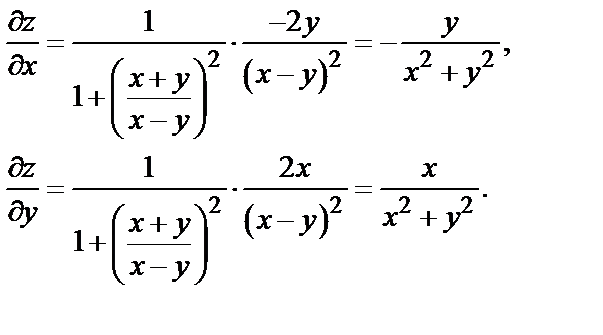
Следовательно, 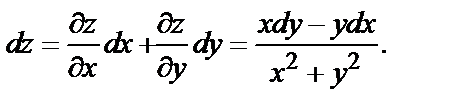
Пример 3. Вычислить приближенно 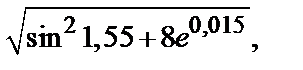 исходя из значения функции
исходя из значения функции 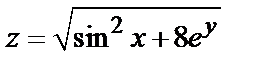 при
при 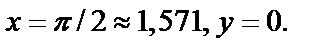
Решение. Искомое число есть наращенное значение функции z при 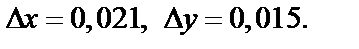 Найдем значение z при
Найдем значение z при 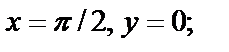 имеем
имеем 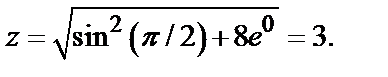
Находим приращение функции:
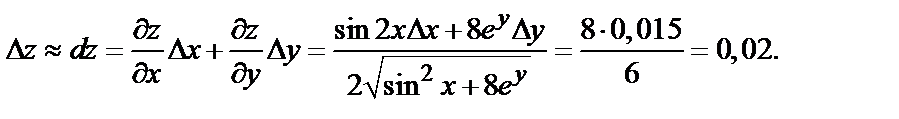
Следовательно, 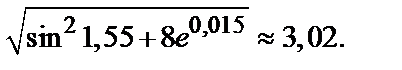
Пример 4. Вычислить приближенно 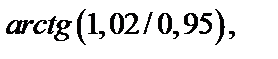 исходя из значения функции
исходя из значения функции 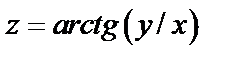 при
при 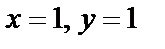 .
.
Решение. Значение функции z при x=1, y=1 есть 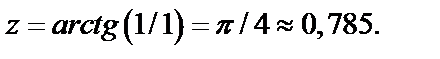
Найдем приращение функции 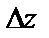 при
при 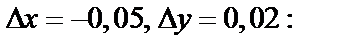
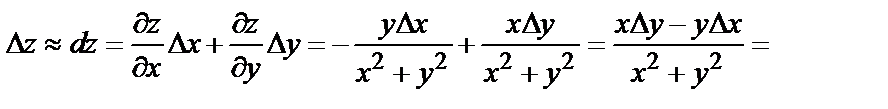
= 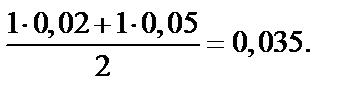
Следовательно, 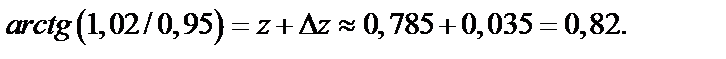
Пример 5. 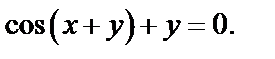 Найти
Найти 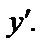
Решение. Здесь 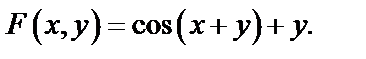
Найдем 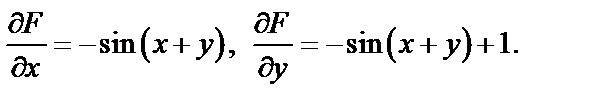
Следовательно,
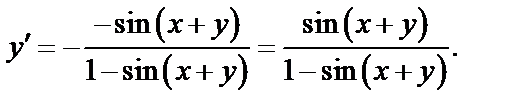
Пример 6. 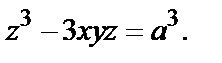 Найти
Найти 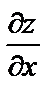 и
и 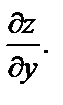
Решение. Здесь 
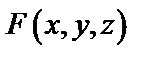 =
= 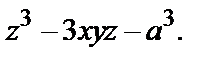
Находим 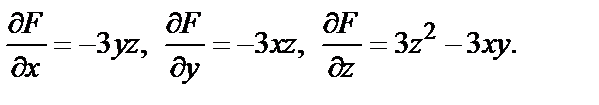
Тогда 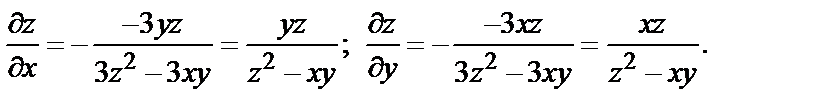
Пример 7. Найти экстремум функции 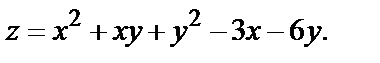
Решение. Находим частные производные первого порядка: 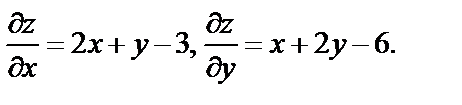 Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
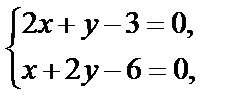 откуда
откуда 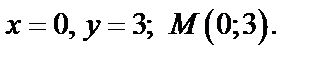
Находим значения частных производных второго порядка в точке M:
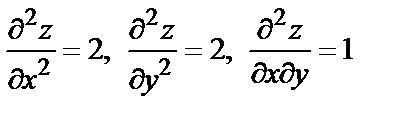
и составляем дискриминант 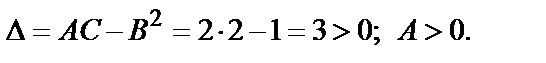 Следовательно, в точке
Следовательно, в точке 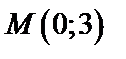 заданная функция имеет минимум. Значение функции в этой точке
заданная функция имеет минимум. Значение функции в этой точке 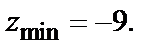
Пример 8. Найти экстремум функции
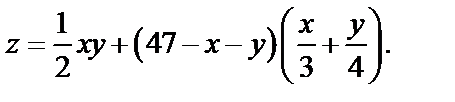
Решение. Находим частные производные первого порядка:
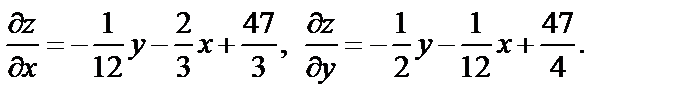
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
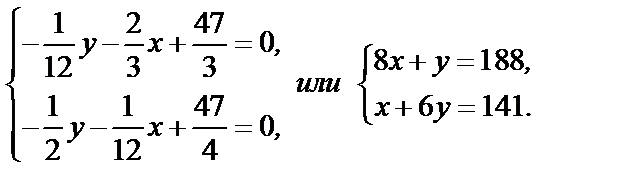
Отсюда x=21, y=20; стационарная точка 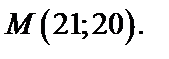
Найдем значения вторых производных в точке M: 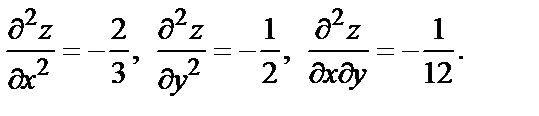
Тогда 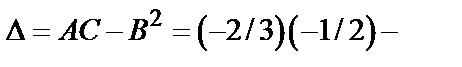
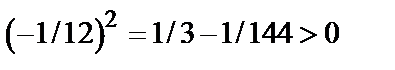 .
.
Так как A<0, то в точке 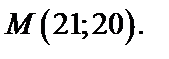 функция имеет максимум:
функция имеет максимум: 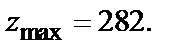
Задачи № 241-270:
Найти частные производные первого порядка 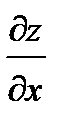 и
и 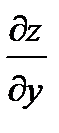 :
:
241. 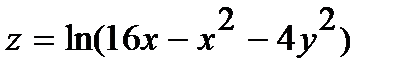 | 256. 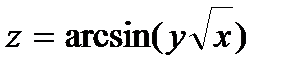 |
242. 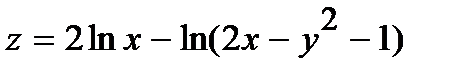 | 257. 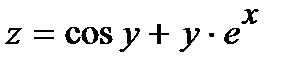 |
243. 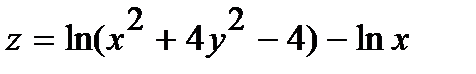 | 258. 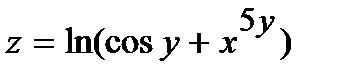 |
244. 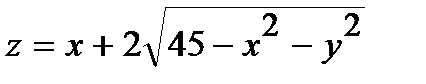 | 259. 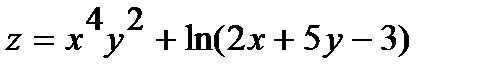 |
245. 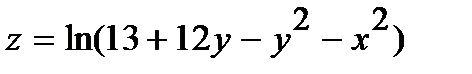 | 260. 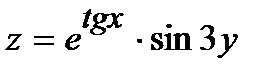 |
246. 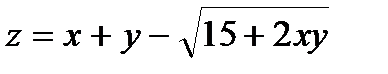 | 261. 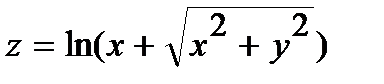 |
247. 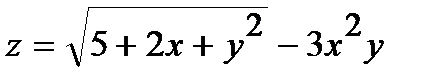 | 262. 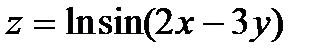 |
248. 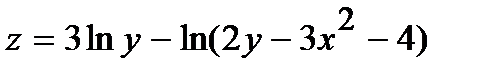 | 263. 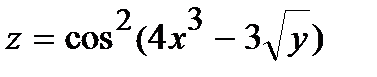 |
249. 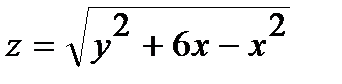 | 264. 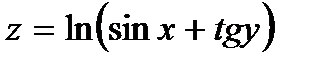 |
250. 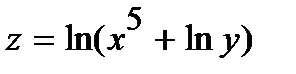 | 265. 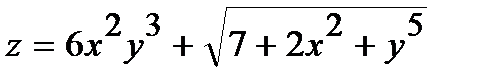 |
251. 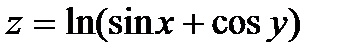 | 266. 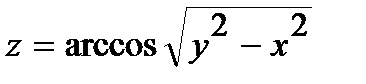 |
252. 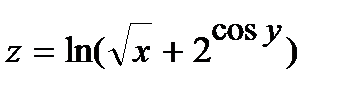 | 267. 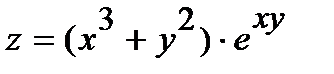 |
253. 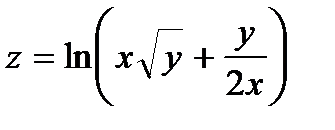 | 268. 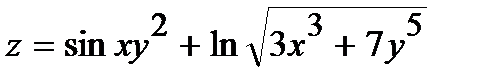 |
254. 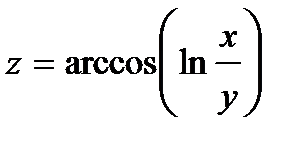 | 269. 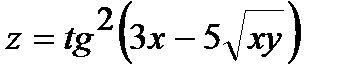 |
255. 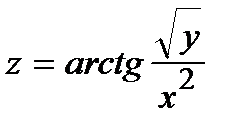 | 270. 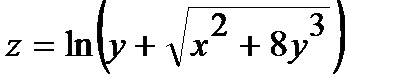 |
Задачи № 271-300:
Вычислить приближенное значение функции 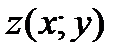 в точке А.
в точке А.
271. 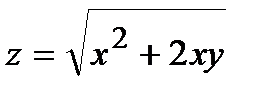 , A(1,94; 3,02) , A(1,94; 3,02) | 286. 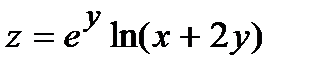 , A(0,98; 0,03) , A(0,98; 0,03) |
272. 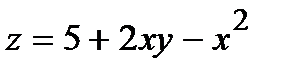 , A(1,98; 3,92) , A(1,98; 3,92) | 287. 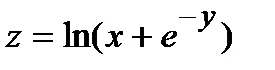 , A(1,04; 0,05) , A(1,04; 0,05) |
273. 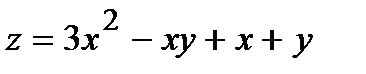 , A(1,06; 2,92) , A(1,06; 2,92) | 288. 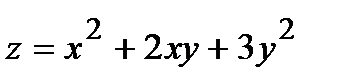 , A(1,96; 1,04) , A(1,96; 1,04) |
274. 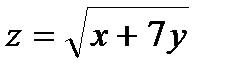 , A(1,94; 1,03) , A(1,94; 1,03) | 289. 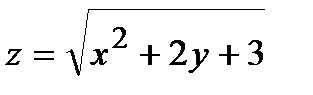 , A(2,02; 0,97) , A(2,02; 0,97) |
275. 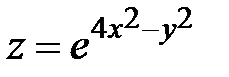 , A(0,98; 2,03) , A(0,98; 2,03) | 290. 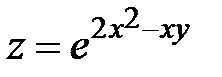 , A(2,03; 3,94) , A(2,03; 3,94) |
276. 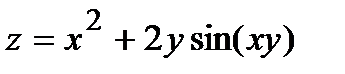 , A(0,05; 1,96) , A(0,05; 1,96) | 291. 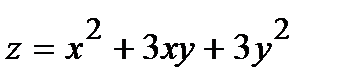 , A(1,98; 1,02) , A(1,98; 1,02) |
277. 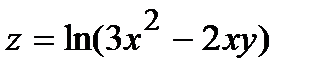 , A(1,03; 0,98) , A(1,03; 0,98) | 292. 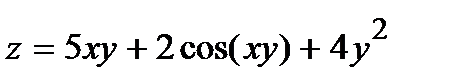 , A(0,05; 2,98) , A(0,05; 2,98) |
278. 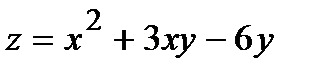 , A(3,96; 1,03) , A(3,96; 1,03) | 293. 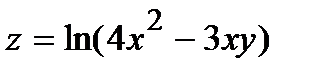 , A(0,96; 1,02) , A(0,96; 1,02) |
279. 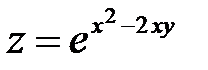 , A(0,05; 2,97) , A(0,05; 2,97) | 294. 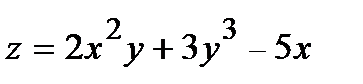 , A(2,04; 1,96) , A(2,04; 1,96) |
280. 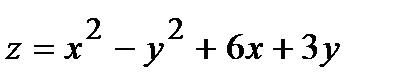 , A(2,02; 2,97) , A(2,02; 2,97) | 295. 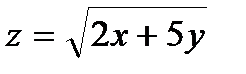 , A(1,97; 1,05) , A(1,97; 1,05) |
281. 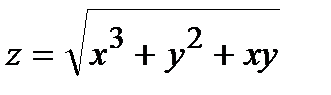 , A(2,06; 1,96) , A(2,06; 1,96) | 296. 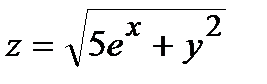 , A(0,02; 2,03) , A(0,02; 2,03) |
282. 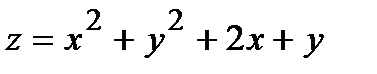 , A(1,98; 3,91) , A(1,98; 3,91) | 297. 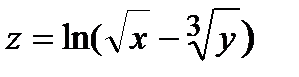 , A(4,03; 0,98) , A(4,03; 0,98) |
283. 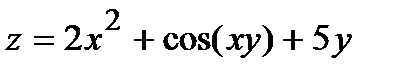 , A(1,99; 0,02) , A(1,99; 0,02) | 298. 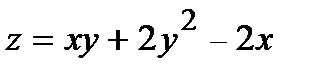 , A(0,97; 2,03) , A(0,97; 2,03) |
284. 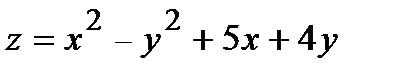 , A(3,05; 1,98) , A(3,05; 1,98) | 299. 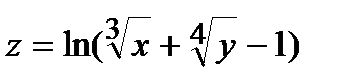 , A(1,03; 0,98) , A(1,03; 0,98) |
285. 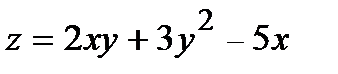 , A(2,04; 3,95) , A(2,04; 3,95) | 300. 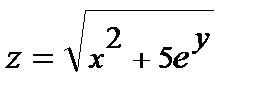 , A(2,04; 0,02) , A(2,04; 0,02) |
Задачи № 301-330:
Найти производную 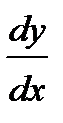 от неявной функции, заданной уравнением.
от неявной функции, заданной уравнением.
301. 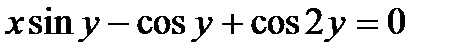 | 316. 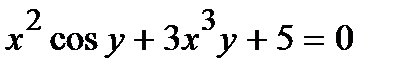 |
302. 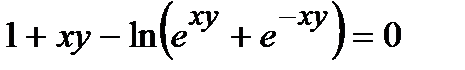 | 317. 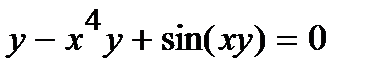 |
303. 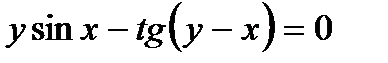 | 318. 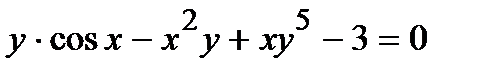 |
304. 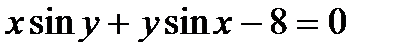 | 319. 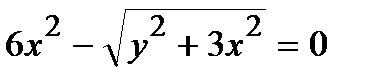 |
305. 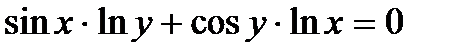 | 320. 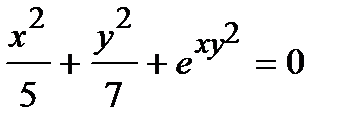 |
306. 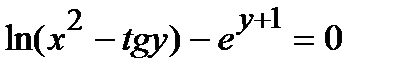 | 321. 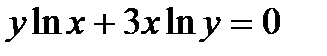 |
307. 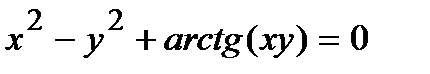 | 322. 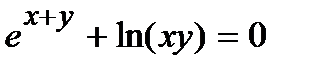 |
308. 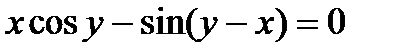 | 323. 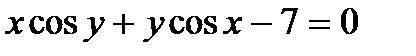 |
309. 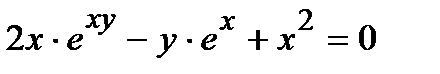 | 324. 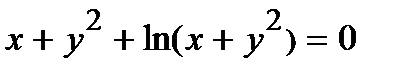 |
310. 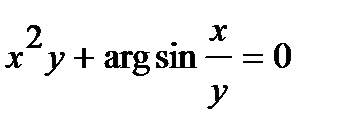 | 325. 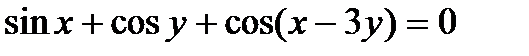 |
311. 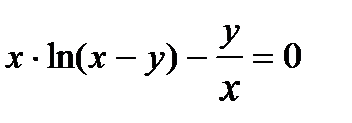 | 326. 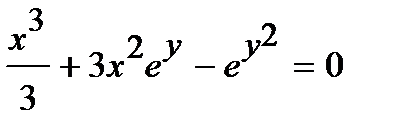 |
312. 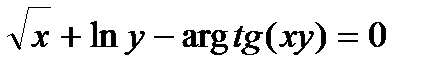 | 327. 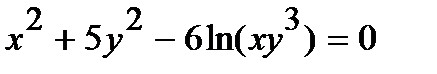 |
313. 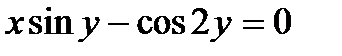 | 328. 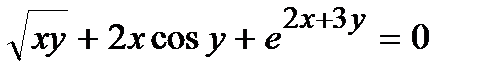 |
314. 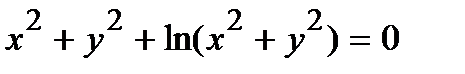 | 329. 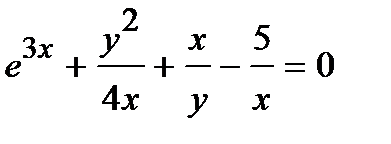 |
315. 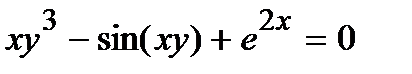 | 330. 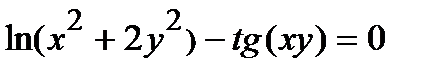 |
Задачи №331-360:
Найти экстремум функции двух переменных 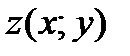 .
.
331. 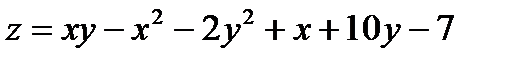 |
332. 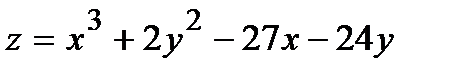 |
333. 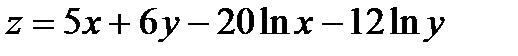 |
334. 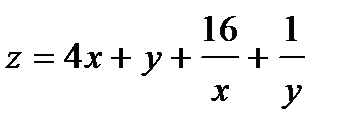 |
335. 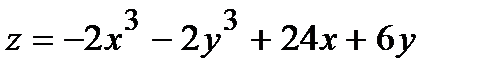 |
336. 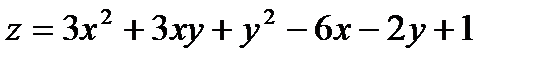 |
337. 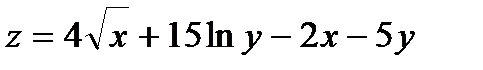 |
338. 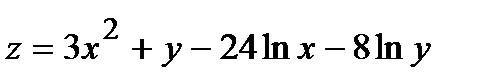 |
339. 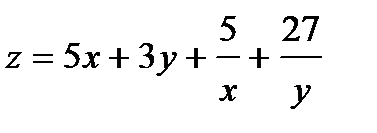 |
340. 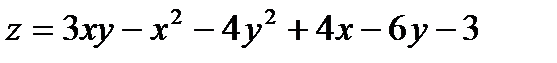 |
341. 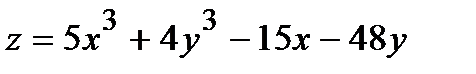 |
342. 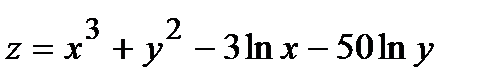 |
343. 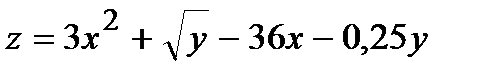 |
344. 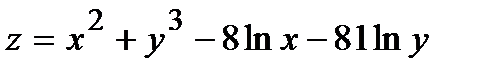 |
345. 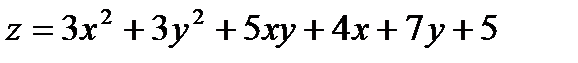 |
346. 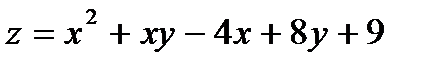 |
347. 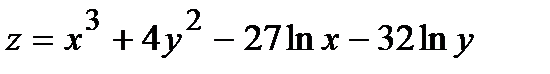 |
348. 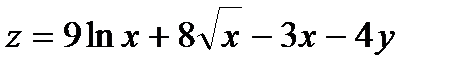 |
349. 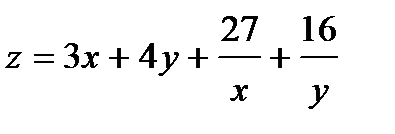 |
350. 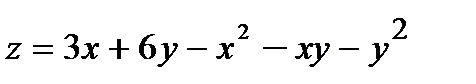 |
351. 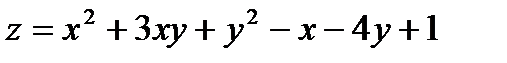 |
352. 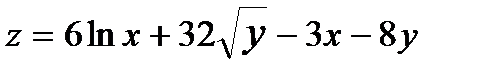 |
353. 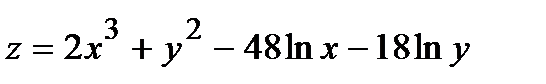 |
354. 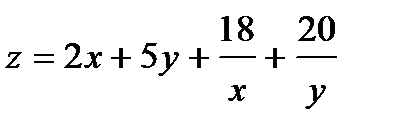 |
355. 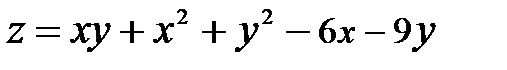 |
356. 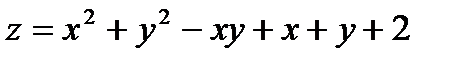 |
357. 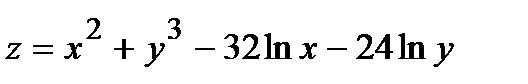 |
358. 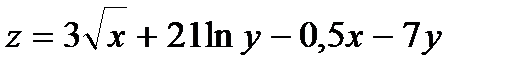 |
359. 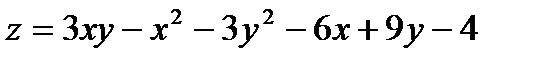 |
360. 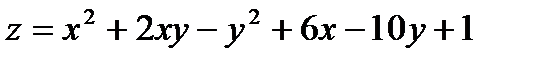 |
Основные понятия
1. Общим решениемдифференциального уравненияпервого порядка называется дифференцируемая функция y= 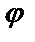 (х,С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y=
(х,С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y=
