Применение простых методов сглаживания измеренных сигналов и подавления шумов в ИИС

Цель работы: Изучение алгоритма оптимального оценивания векторных физических величие на основе метода наименьших квадратов при векторных измерениях в условиях воздействия аддитивных шумов. Изучение численных методов оценивания.

Задание

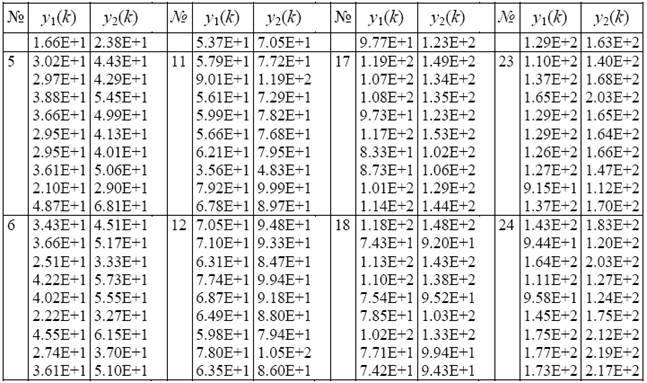
1. Найти оптимальную весовую матрицу алгоритма оценивания векторной физической величины на основе метода наименьших квадратов ( исходные данные представлены в табл. 1.1 и 1.2).

2. Получить оптимальную оценку вектора Х в дискретном времени.

3. Рассчитать корреляционную матрицу ошибок оценивания.

4. Рассчитать среднеквадратические ошибки оценок.

5. Ответить на контрольные вопросы.

Таблица 1.1

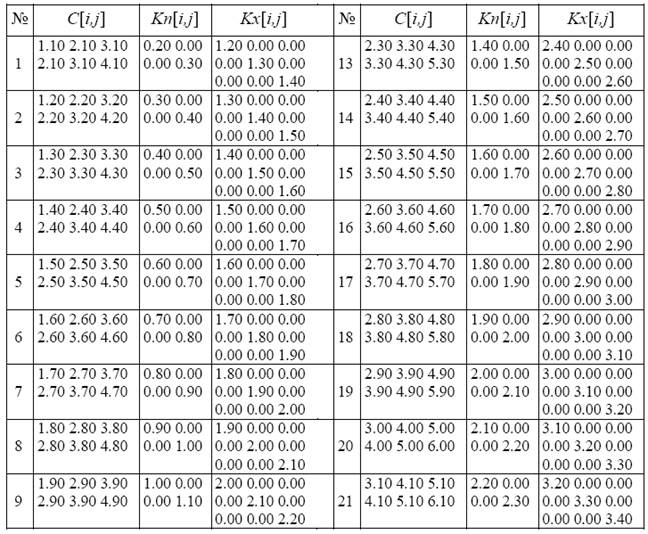
Окончание табл. 1.1

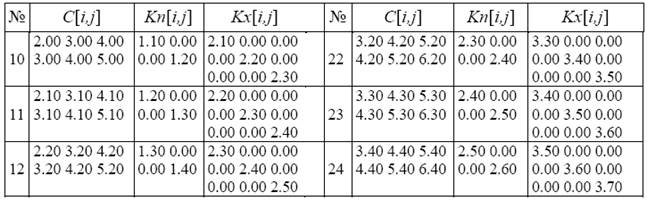
Таблица 1.2

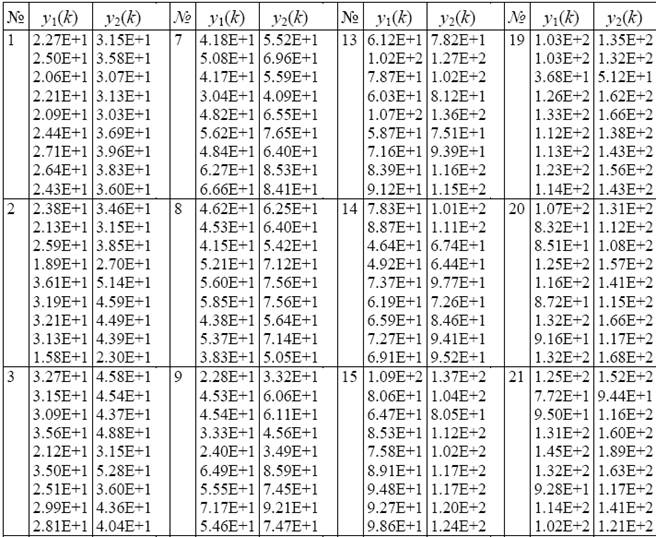
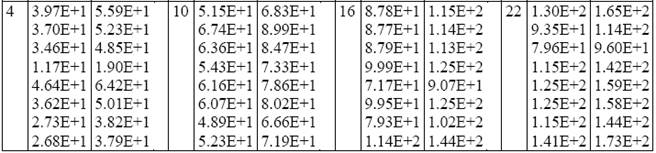
Окончание табл. 1.2

Порядок выполнения работы

Приведем пример автоматизированного расчета с помощью пакета программ CAD-MS [1]. Примеры расчета с помощью калькулятора и электронных таблиц Excel приведены в [2].

Пример. Оценивается вектор физических величин Х, состоящий из 3-х компонент. Уравнение измерений Y=CX+N имеет вид

.

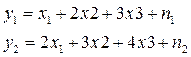Заданы корреляционные матрицы оцениваемого вектора Х и вектора шума N.

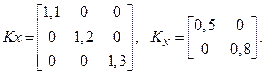
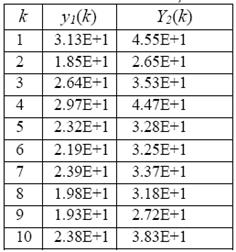
Производится оценивание вектора X в дискретном времени в процессе измерений по 10 последовательным шагам. Результаты измерений при
k =1, ..., 10 заданы в табл. 1.3.

Проектирование алгоритма и вычислительный эксперимент (моделирование) выполнено программой Filtr-Gs.exe, исходные данные - в файле Mnk-i.dat, результаты получены в файле Mnk-r.dat.

Таблица 1.3

1. Найдена оптимальная весовая матрица алгоритма оценивания векторной физической величины X(k/k) = GY(k)на основе метода наименьших квадратов (формула (3.29) [2]):

G=K_XC^T{CK_XC^T+K_N}^-1.

-3,53Е-1 3,00Е-1

-4,09Е-2 1,26Е-1

3,29Е-1 -8,23Е-2

2. Получена оптимальная оценка вектора Х в дискретном времени (формула (3.26) [2]): X(k/k) = GY(k) (табл.1.4).

Таблица 1.4

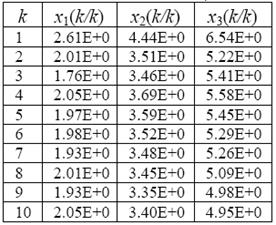3. Рассчитана корреляционная матрица ошибок оценивания (формула (3.31) [2]):

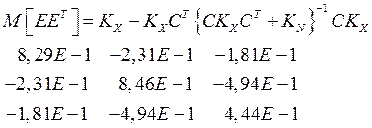
4. Рассчитаны среднеквадратические ошибки оценок: s₁ = 0,91. s₂ = 0,92, s₃ = 0,67.

Вывод. На основе полученной корреляционной матрицы, дисперсии оценок составляют: D₁ = 0,83: D₂ = 0,846: D₃ = 0,444.Это меньше соответствующих дисперсий исходных физических величин: Кх₁₁ = 1,1; Кх₂₂ = 1,2; Кх₃₃ = 1,3. Оптимальное оценивание дает выигрыш в точности: для х₁в (Кх₁₁/D₁)^0,5 = l,15 раза; для х₂в 1,19; для х₃- в 1,71.

Контрольные вопросы

1. Поясните уравнение измерений при оптимальном оценивании векторных физических величин на основе метода наименьших квадратов.

2. Дайте определение корреляционной матрицы шумов измерений.

3. Какие априорные сведения необходимы для данной задачи оценивания?

4. Как определить матрицу С уравнения измерений на основе испытаний?

5. Как связана оптимальная оценка Х(k/k)вектора физических величин Х(к)с вектором измерений?

6. В чем заключается условие минимума среднего квадрата ошибок оценивания для j-й компоненты вектора физических величин Х(k)?

7. Запишите формулу для вычисления матрицы линейного преобразования G.

8. Как определяется корреляционная матрица ошибок оценивания?

9. Запишите результирующее выражение для расчета оптимальной оценки Х(k/k)вектора физических величин Х(k).

10. Приведите алгоритм решения задачи оптимального оценивания векторных физических величин на основе метода наименьших квадратов.

11. Может ли быть число оцениваемых компонент вектора X больше числа уравнений измерений?

12. Как практически рассчитать коэффициенты матрицы линейного преобразования G=K_XC^T{CK_XC^T+K_N)^-1?

13. Как практически рассчитать оценку вектора физических величин X(k/k)=GY(k)?

14. Как практически рассчитать корреляционную матрицу ошибок оценивания M[EE^T] = K_XK_XC^T{CK_X+K_N)^-1CK_X ?

15. Каковы особенности расчета при использовании таблиц Excel?

Лабораторная работа 2

Вычисление функции корреляции

Цель работы - научиться использовать возможности MS Excel для проведения корреляционного и регрессионного анализа исследовательских данных, планирования и обработки результатов факторного эксперимента.

Учебные вопросы:

1. Возможности прикладного программного обеспечения на этапах обработки и оценки результатов исследования.

Изучив данную тему, студент должен:

знать:

- назначение существующих современных средств компьютеризации научных исследований, их функциональные возможности и особенности применения;

уметь:

- производить обработку и оценку результатов исследования.

1.1. Краткое изложение основных теоретических и методических аспектов работы

Параметрический корреляционный анализ

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками (наборами числовых данных каких-либо величин). Обычно связь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей различают корреляцию и регрессию.

Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема n связанных пар наблюдений (x_it yi) из совместной генеральной совокупности X и Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин X и Y.

Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону.

Линейный коэффициент корреляции - параметр, который характеризует степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле:

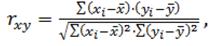(1)

где x_i – значения, принимаемые в выборке X,

y_i – значения, принимаемые в выборке Y;

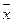- средняя по X, 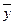- средняя по Y.

Таблица 1. Теснота связи и величина коэффициента корреляции

Коэффициент корреляции rxy	Теснота связи
+( 0,91 ... 1,00)	Очень сильная
±( 0,81 ... 0,90)	Весьма сильная
± (0,65 … 0,80)	Сильная
± (0,45 … 0,64)	Умеренная
± (0,25 … 0,44)	Слабая
до ± 0,25	Очень слабая
«+»– прямая зависимость «–» – обратная зависимость

Коэффициент корреляции изменяется от -1 до 1. Когда при расчете получается величина большая +1 или меньшая -1 - следовательно, произошла ошибка в вычислениях. При значении 0 линейной зависимости между двумя выборками нет.

Знак коэффициента корреляции очень важен для интерпретации полученной связи (таблица 1). Если знак коэффициента линейной корреляции «+», то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости.

t-статистика Стьюдента

Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистику Стьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратическому отклонению и рассчитывается по формуле (2)

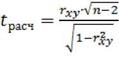(2)

Полученную величину t_pacч сравнивают с табличным значением t критерия Стьюдента с n - 2 степенями свободы. Если t_pacч > t_табл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин X и Y в выборке из генеральной совокупности, т.е. существует зависимость между X и Y. И наоборот, если t_pacч < t_табл, то величины X и Y независимы.

Исследование связей между двумя переменными в Excel

Условие задачи: По 10 Интернет-магазинам были определены затраты на рекламную раскрутку сайтов и количество покупателей, воспользовавшихся после ее проведения услугами каждого магазина. Определить коэффициент корреляции между исследуемыми признаками.

Ход выполнения:

25. Открываем новую книгу MS Excel и создаем таблицу согласно рис. 2.

26. Рассчитываем в ячейке С12 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические.

Синтаксис функции: КОРРЕЛ (<массив 1>;<массив 2>),

где <массив 1> – ссылка на диапазон ячеек первой выборки (X);

<массив 2> – ссылка на диапазон ячеек второй выборки (Y).

В нашей задаче формула будет иметь вид: =КОРРЕЛ(В2:В11;С2:С11) – см. рис. 3.

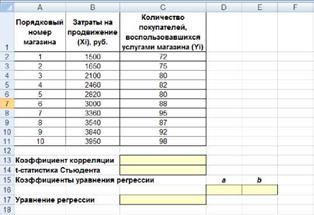
Рисунок 2. Исходные данные для исследования связей между двумя переменными

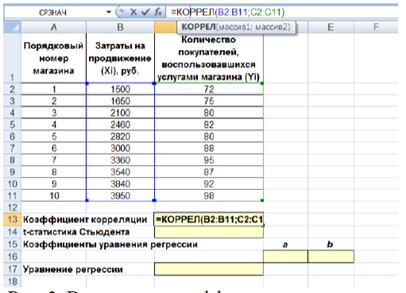
Рисунок 3. Вычисление коэффициента корреляции

27. Сделаем вывод о тесноте связи между затратами на рекламную раскрутку сайтов и количество покупателей.

После ввода формулы получаем в ячейке C13 значение коэффициента корреляции равное 0,93. По таблице 2 делаем вывод, что связь между переменными очень сильная, т.е. имеет место линейная зависимость (прямая пропорциональность).

28.

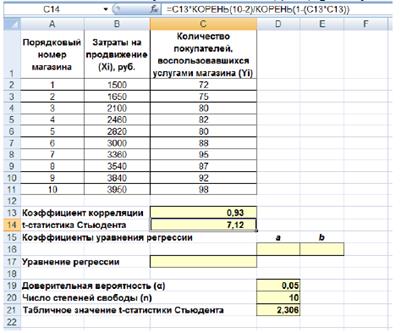Оценим значимость коэффициента корреляции. С этой целью рассмотрим две гипотезы. Основную Н₀: r_xу = 0 и альтернативную H₁: r_xy ≠ 0. Для проверки гипотезы Н₀ рассчитаем в ячейке С14 t-статистику Стьюдента по формуле, указанной в 3.1.2. В нашем случае число степеней свободы v = n – 2 = 10 – 2 = 8 и формула будет следующей: =С13*КОРЕНЬ(10-2)/КОРЕНЬ(1-(С13*С13)). После ввода формулы получаем в ячейке С13 t-статистику Стьюдента (t_pacч) равную 7,12 (рис. 4).

Рисунок 4. Вычисление t-статистики Стьюдента (t_pacч)

29. Сравним полученное значение с критическим значением t _{v,α табл} распределения Стьюдента (при v = 8 и доверительной вероятности α = 0,05, t _{v,α табл} = 2,306). t _{v,α табл} можно найти либо в специальной таблице (приложение 1), либо воспользовавшись встроенной статистической функцией СТЬЮДРАСПОБР(вероятность; степени_свободы). В нашем случае это будет формула: =СТЬЮДРАСПОБР(D19;D20-2).

30. Сделаем вывод о наличии связи между исследуемыми величинами – так как t_расч > t _{v,α табл} (7,12 > 2,306), то между переменными существует зависимость и найденный коэффициент корреляции значим.

Регрессионный анализ

Цель регрессионного анализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели (например, полиномиальные и экспоненциальные). В данной работе изучим линейную модель.

Уравнение линейной регрессии имеет вид:

Y = a₁X₁ + a₂X₂ + ...+ a_kX_k,

где a₁, а₂, ..., a_k – параметры, подлежащие определению методом наименьших квадратов (МНК).

Обычно находят первые два параметра, которые принято обозначать а и b. В этом случае уравнение линейной регрессии имеет вид Y = a·X + b.

Коэффициенты а и b вычисляются следующим образом (формулы 3 – 4):

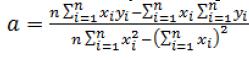(3)

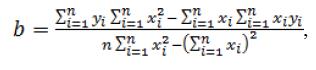
(4)

где i – номер измерения, x_i и у_i – значения переменных при i-том измерении, n - число измерений при моделировании системы.

В среде MS Excel для нахождения модели регрессии (т.е., фактически коэффициентов а и b) можно использовать несколько способов:

- использовать встроенную функцию ЛИНЕИН;

- графический способ – построение линии тренда на диаграмме с показом уравнения регрессии;

- инструмент Регрессия из Пакета анализа;

- использовать встроенную функцию СУММКВРАЗН и инструмент Поиск решения:

- использовать встроенные функции НАКЛОН (вычисляет коэффициент а) и

- ОТРЕЗОК (вычисляет коэффициент b).

Построение регрессионной модели средствами Excel

Рассмотрим на примере первые три из перечисленных способов нахождения модели регрессии.

Й способ. Функция ЛИНЕЙН.

В первом способе для получения коэффициентов а и b линейного уравнения регрессии Y = a·X + b, описывающего зависимость количества привлеченных покупателей от затрат на рекламную раскрутку сайтов, воспользуемся статистической функцией ЛИНЕИН. Для этого выделите две ячейки D16:E16 и выполните вставку функции ЛИНЕИН с аргументами согласно рис. 5.

Рисунок 5. Аргументы функции ЛИНЕЙН

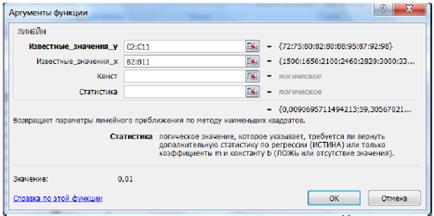Здесь «Известные_значения_у» – диапазон значений «Количество покупателей», «Известные_значения_х» - диапазон значений «Затраты на продвижение». Нажмите комбинацию клавиш SHIFT+CTRL+ENTER.

Получаем следующие значения коэффициентов регрессии – a = 0,01 (ячейка D16), b = 59,32 (ячейка E16). В ячейку D17 введем уравнение Y = 0,01X + 59,31, чтобы продемонстрировать уравнение регрессии: