По выполнению лабораторных работ

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ

«Информационно-измерительные системы»

основной образовательной программы подготовки бакалавров

по направлению 09.03.01 Информатика и вычислительная техника

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

По выполнению лабораторных работ

Лысьва 2016 г.

Методические указания к лабораторным работам по дисциплинам «Информационно-измерительные системы» рассмотрены и утверждены на заседании кафедры естественнонаучных дисциплин «___» ____________201_ г. Протокол № ______ от «___» ____ . 201_ .

Разработал

Доцент ЛФ ПНИПУ В.Г. Лопатин

Информационно-измерительные системы: Методические указания по выполнению лабораторных работ / сост. В.Г. Лопатин. Пермский национальный исследовательский политехнический университет. Лысьвенский филиал. Лысьва, 2016.

Настоящие методические указания разработаны в соответствии с требованиями государственных образовательных стандартов высшего профессионального образования по направлению подготовки бакалавров 09.03.01 Информатика и вычислительная техника.

Методические указания предназначены для студентов всех форм обучения для предварительной подготовки и выполнения лабораторных работ по дисциплине «Информационно-измерительные системы».

Рецензент: к.т.н., доцент Е.М.Васильев

	© Пермский национальный исследовательский политехнический университет,
	Лысьвенский филиал, 2016.

СОДЕРЖАНИЕ

Введение
1. Цель лабораторных занятий
2. Правила безопасной работы
3. Домашняя подготовка
4. Выполнение лабораторной работы
5. Оформление отчета
6. Образец выполнение отчета
Лабораторная работа № 1. Применение простых методов сглаживания измеренных сигналов и подавления шумов в ИИС. . . . . . . . . . . . . . . . . . . . . . . .
Лабораторная работа № 2. Вычисление функции корреляции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Лабораторная работа № 3. Моделирование аналого-цифрового преобразования.
Лабораторная работа № 4. Изучение временных характеристик типовых динамических звеньев . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Лабораторная работа № 5. Исследование влияния обратной связи на систему. . . . . . . . . . . . . . . . . . . . .
Лабораторная работа № 6. Анализ качества регулирования линейных систем.
Лабораторная работа № 7. Преобразования структурных схем. . . . . . . . . . . . . . . . . . . . . . . . .
Лабораторная работа № 8. Построение информационно-измерительной системы реального объекта. . . . . . . . . . . . . . . . . . . . . .
Рекомендуемая литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

- Цель дисциплины - формирование комплекса знаний, умений и навыков по основам построения и функционирования информационно-измерительных систем (ИИС).

В процессе изучения данной дисциплины студент осваивает следующие компетенции:

- способность выполнять проектирование и обоснование функциональнологической структуры вычислительных систем и сетей (ПСК-3).

- Задачи дисциплины:

1. Изучение:

2. основных понятий, терминов и определений в области информационноизмерительных систем (ИИС);

3. структуры информационно-измерительных систем;

4. методов сглаживания сигналов и подавления шумов;

5. способов вычисления корреляции;

6. принципов вычисления соотношения «сигнал-шум»;

7. методов построения гистограмм;

8. принципов аналого-цифрового преобразования;

9. способов цифровой фильтрации;

10. современных технологий в информационно-измерительных системах.

11. Формирование умений:

12. моделирования аналого-цифрового преобразования;

13. выполнения дискретных преобразований;

14. моделирования и расчета цифровых фильтров в ИИС;

15. моделирования работы и вычисления параметров функционирования ИИС.

16. Формирование навыков:

17. применения простых методов сглаживания измеренных сигналов и подавления шумов в ИИС;

18. вычисления функции корреляции;

19. вычисления соотношения «сигнал-шум» (SNR) и коэффициента изменчивости

(CV);

20. построения гистограмм, функций вероятностной меры и плотности вероятности.

- Предметом освоения дисциплины являются следующие объекты:

21. системы сбора и обработки данных,

22. робототехнические системы,

23. встраиваемые системы,

24. программно-технические средства ИИС.

- Место дисциплины в структуре профессиональной подготовки выпускников.

Дисциплина «Информационно-измерительные системы» относится к вариативной части цикла профессиональных дисциплин и является дисциплиной по выбору при освоении ООП по направлению 230100.62 «Информатика и вычислительная техника», профилю «Вычислительные машины, комплексы, системы и сети».

После изучения дисциплины обучающийся должен освоить части указанных в пункте 1.1 компетенций и демонстрировать следующие результаты: знать:

- основные понятия, термины и определения в области информационно-измерительных систем (ИИС);

- структуру информационно-измерительных систем;

- методы сглаживания сигналов и подавления шумов;

- способы вычисления корреляции;

- принципы вычисления соотношения «сигнал-шум»;

- методы построения гистограмм;

- принципы аналого-цифрового преобразования;

- способы цифровой фильтрации;

- современные технологии в информационно-измерительных системах;

уметь:

- моделировать аналого-цифровое преобразование;

- выполнять дискретные преобразования;

- моделировать и рассчитывать цифровые фильтры в ИИС;

- моделировать работу и вычислять параметры функционирования ИИС;

владеть навыками:

- применения простых методов сглаживания измеренных сигналов и подавления шумов в иис;

- вычисления функции корреляции;

- вычисления соотношения «сигнал-шум» (snr) и коэффициента изменчивости (cv);

- построения гистограмм, функций вероятностной меры и плотности вероятности.

Лабораторная работа 1

Порядок выполнения работы

Приведем пример автоматизированного расчета с помощью пакета программ CAD-MS [1]. Примеры расчета с помощью калькулятора и электронных таблиц Excel приведены в [2].

Пример. Оценивается вектор физических величин Х, состоящий из 3-х компонент. Уравнение измерений Y=CX+N имеет вид

.

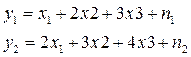Заданы корреляционные матрицы оцениваемого вектора Х и вектора шума N.

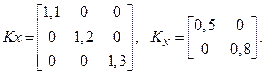
Производится оценивание вектора X в дискретном времени в процессе измерений по 10 последовательным шагам. Результаты измерений при
k =1, ..., 10 заданы в табл. 1.3.

Проектирование алгоритма и вычислительный эксперимент (моделирование) выполнено программой Filtr-Gs.exe, исходные данные - в файле Mnk-i.dat, результаты получены в файле Mnk-r.dat.

Таблица 1.3

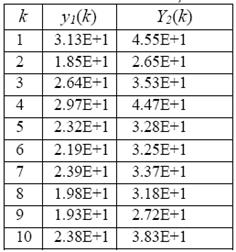1. Найдена оптимальная весовая матрица алгоритма оценивания векторной физической величины X(k/k) = GY(k)на основе метода наименьших квадратов (формула (3.29) [2]):

G=K_XC^T{CK_XC^T+K_N}^-1.

-3,53Е-1 3,00Е-1

-4,09Е-2 1,26Е-1

3,29Е-1 -8,23Е-2

2. Получена оптимальная оценка вектора Х в дискретном времени (формула (3.26) [2]): X(k/k) = GY(k) (табл.1.4).

Таблица 1.4

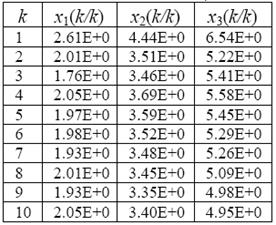3. Рассчитана корреляционная матрица ошибок оценивания (формула (3.31) [2]):

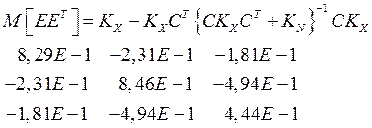
4. Рассчитаны среднеквадратические ошибки оценок: s₁ = 0,91. s₂ = 0,92, s₃ = 0,67.

Вывод. На основе полученной корреляционной матрицы, дисперсии оценок составляют: D₁ = 0,83: D₂ = 0,846: D₃ = 0,444.Это меньше соответствующих дисперсий исходных физических величин: Кх₁₁ = 1,1; Кх₂₂ = 1,2; Кх₃₃ = 1,3. Оптимальное оценивание дает выигрыш в точности: для х₁в (Кх₁₁/D₁)^0,5 = l,15 раза; для х₂в 1,19; для х₃- в 1,71.

Контрольные вопросы

1. Поясните уравнение измерений при оптимальном оценивании векторных физических величин на основе метода наименьших квадратов.

2. Дайте определение корреляционной матрицы шумов измерений.

3. Какие априорные сведения необходимы для данной задачи оценивания?

4. Как определить матрицу С уравнения измерений на основе испытаний?

5. Как связана оптимальная оценка Х(k/k)вектора физических величин Х(к)с вектором измерений?

6. В чем заключается условие минимума среднего квадрата ошибок оценивания для j-й компоненты вектора физических величин Х(k)?

7. Запишите формулу для вычисления матрицы линейного преобразования G.

8. Как определяется корреляционная матрица ошибок оценивания?

9. Запишите результирующее выражение для расчета оптимальной оценки Х(k/k)вектора физических величин Х(k).

10. Приведите алгоритм решения задачи оптимального оценивания векторных физических величин на основе метода наименьших квадратов.

11. Может ли быть число оцениваемых компонент вектора X больше числа уравнений измерений?

12. Как практически рассчитать коэффициенты матрицы линейного преобразования G=K_XC^T{CK_XC^T+K_N)^-1?

13. Как практически рассчитать оценку вектора физических величин X(k/k)=GY(k)?

14. Как практически рассчитать корреляционную матрицу ошибок оценивания M[EE^T] = K_XK_XC^T{CK_X+K_N)^-1CK_X ?

15. Каковы особенности расчета при использовании таблиц Excel?

Лабораторная работа 2

Вычисление функции корреляции

Цель работы - научиться использовать возможности MS Excel для проведения корреляционного и регрессионного анализа исследовательских данных, планирования и обработки результатов факторного эксперимента.

Учебные вопросы:

1. Возможности прикладного программного обеспечения на этапах обработки и оценки результатов исследования.

Изучив данную тему, студент должен:

знать:

- назначение существующих современных средств компьютеризации научных исследований, их функциональные возможности и особенности применения;

уметь:

- производить обработку и оценку результатов исследования.

1.1. Краткое изложение основных теоретических и методических аспектов работы

Параметрический корреляционный анализ

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками (наборами числовых данных каких-либо величин). Обычно связь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей различают корреляцию и регрессию.

Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема n связанных пар наблюдений (x_it yi) из совместной генеральной совокупности X и Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин X и Y.

Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону.

Линейный коэффициент корреляции - параметр, который характеризует степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле:

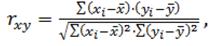(1)

где x_i – значения, принимаемые в выборке X,

y_i – значения, принимаемые в выборке Y;

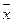- средняя по X, 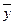- средняя по Y.

Таблица 1. Теснота связи и величина коэффициента корреляции

Коэффициент корреляции rxy	Теснота связи
+( 0,91 ... 1,00)	Очень сильная
±( 0,81 ... 0,90)	Весьма сильная
± (0,65 … 0,80)	Сильная
± (0,45 … 0,64)	Умеренная
± (0,25 … 0,44)	Слабая
до ± 0,25	Очень слабая
«+»– прямая зависимость «–» – обратная зависимость

Коэффициент корреляции изменяется от -1 до 1. Когда при расчете получается величина большая +1 или меньшая -1 - следовательно, произошла ошибка в вычислениях. При значении 0 линейной зависимости между двумя выборками нет.

Знак коэффициента корреляции очень важен для интерпретации полученной связи (таблица 1). Если знак коэффициента линейной корреляции «+», то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости.

t-статистика Стьюдента

Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистику Стьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратическому отклонению и рассчитывается по формуле 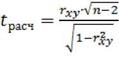(2)

(2)

Полученную величину t_pacч сравнивают с табличным значением t критерия Стьюдента с n - 2 степенями свободы. Если t_pacч > t_табл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин X и Y в выборке из генеральной совокупности, т.е. существует зависимость между X и Y. И наоборот, если t_pacч < t_табл, то величины X и Y независимы.

Исследование связей между двумя переменными в Excel

Условие задачи: По 10 Интернет-магазинам были определены затраты на рекламную раскрутку сайтов и количество покупателей, воспользовавшихся после ее проведения услугами каждого магазина. Определить коэффициент корреляции между исследуемыми признаками.

Ход выполнения:

25. Открываем новую книгу MS Excel и создаем таблицу согласно рис. 2.

26. Рассчитываем в ячейке С12 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические.

Синтаксис функции: КОРРЕЛ (<массив 1>;<массив 2>),

где <массив 1> – ссылка на диапазон ячеек первой выборки (X);

<массив 2> – ссылка на диапазон ячеек второй выборки (Y).

В нашей задаче формула будет иметь вид: =КОРРЕЛ(В2:В11;С2:С11) – см. рис. 3.

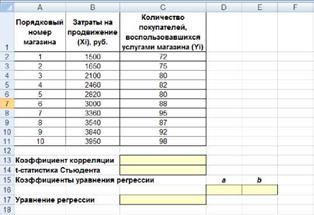
Рисунок 2. Исходные данные для исследования связей между двумя переменными

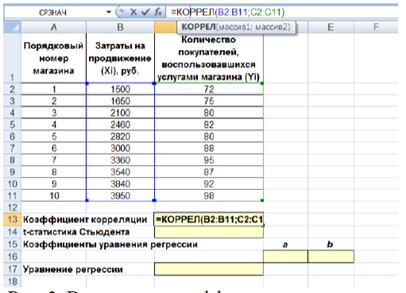
Рисунок 3. Вычисление коэффициента корреляции

27. Сделаем вывод о тесноте связи между затратами на рекламную раскрутку сайтов и количество покупателей.

После ввода формулы получаем в ячейке C13 значение коэффициента корреляции равное 0,93. По таблице 2 делаем вывод, что связь между переменными очень сильная, т.е. имеет место линейная зависимость (прямая пропорциональность).

28.

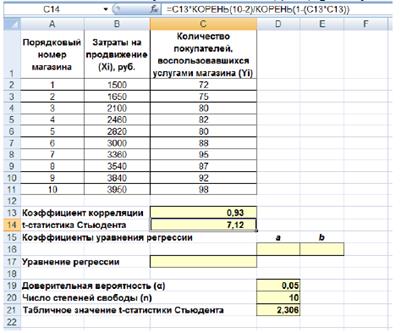Оценим значимость коэффициента корреляции. С этой целью рассмотрим две гипотезы. Основную Н₀: r_xу = 0 и альтернативную H₁: r_xy ≠ 0. Для проверки гипотезы Н₀ рассчитаем в ячейке С14 t-статистику Стьюдента по формуле, указанной в 3.1.2. В нашем случае число степеней свободы v = n – 2 = 10 – 2 = 8 и формула будет следующей: =С13*КОРЕНЬ(10-2)/КОРЕНЬ(1-(С13*С13)). После ввода формулы получаем в ячейке С13 t-статистику Стьюдента (t_pacч) равную 7,12 (рис. 4).

Рисунок 4. Вычисление t-статистики Стьюдента (t_pacч)

29. Сравним полученное значение с критическим значением t _{v,α табл} распределения Стьюдента (при v = 8 и доверительной вероятности α = 0,05, t _{v,α табл} = 2,306). t _{v,α табл} можно найти либо в специальной таблице (приложение 1), либо воспользовавшись встроенной статистической функцией СТЬЮДРАСПОБР(вероятность; степени_свободы). В нашем случае это будет формула: =СТЬЮДРАСПОБР(D19;D20-2).

30. Сделаем вывод о наличии связи между исследуемыми величинами – так как t_расч > t _{v,α табл} (7,12 > 2,306), то между переменными существует зависимость и найденный коэффициент корреляции значим.

Регрессионный анализ

Цель регрессионного анализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели (например, полиномиальные и экспоненциальные). В данной работе изучим линейную модель.

Уравнение линейной регрессии имеет вид:

Y = a₁X₁ + a₂X₂ + ...+ a_kX_k,

где a₁, а₂, ..., a_k – параметры, подлежащие определению методом наименьших квадратов (МНК).

Обычно находят первые два параметра, которые принято обозначать а и b. В этом случае уравнение линейной регрессии имеет вид Y = a·X + b.

Коэффициенты а и b вычисляются следующим образом (формулы 3 – 4):

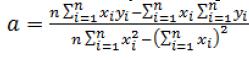(3)

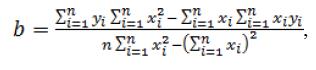
(4)

где i – номер измерения, x_i и у_i – значения переменных при i-том измерении, n - число измерений при моделировании системы.

В среде MS Excel для нахождения модели регрессии (т.е., фактически коэффициентов а и b) можно использовать несколько способов:

- использовать встроенную функцию ЛИНЕИН;

- графический способ – построение линии тренда на диаграмме с показом уравнения регрессии;

- инструмент Регрессия из Пакета анализа;

- использовать встроенную функцию СУММКВРАЗН и инструмент Поиск решения:

- использовать встроенные функции НАКЛОН (вычисляет коэффициент а) и

- ОТРЕЗОК (вычисляет коэффициент b).

Построение регрессионной модели средствами Excel

Рассмотрим на примере первые три из перечисленных способов нахождения модели регрессии.

Й способ. Функция ЛИНЕЙН.

В первом способе для получения коэффициентов а и b линейного уравнения регрессии Y = a·X + b, описывающего зависимость количества привлеченных покупателей от затрат на рекламную раскрутку сайтов, воспользуемся статистической функцией ЛИНЕИН. Для этого выделите две ячейки D16:E16 и выполните вставку функции ЛИНЕИН с аргументами согласно рис. 5.

Рисунок 5. Аргументы функции ЛИНЕЙН

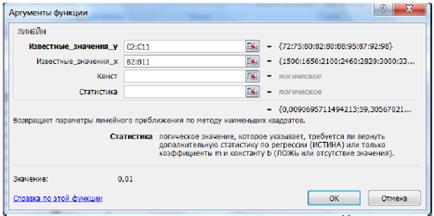Здесь «Известные_значения_у» – диапазон значений «Количество покупателей», «Известные_значения_х» - диапазон значений «Затраты на продвижение». Нажмите комбинацию клавиш SHIFT+CTRL+ENTER.

Получаем следующие значения коэффициентов регрессии – a = 0,01 (ячейка D16), b = 59,32 (ячейка E16). В ячейку D17 введем уравнение Y = 0,01X + 59,31, чтобы продемонстрировать уравнение регрессии:

Лабораторная работа 3

Моделирование аналого-цифрового преобразования

Среди большого числа пакетов прикладных программ система МАТЛАБ (The Math Works Inc.) занимает особое место. Первоначально ориентированная на исследовательские проекты, система в последние годы стала рабочим инструментом не только ученых, но также инженеров-разработчиков и студентов. В сообществе радиоинженеров, управленцев, физиков и связистов МАТЛАБ получил необычайное распространение и по сути стал средством междисциплинарного и международного общения. Особенно широко, эффектно и эффективно система МАТЛАБ применяется в области обработки сигналов, которая по необходимости затрагивает информатику и связь, управление, радиолокацию и радионавигацию, радиовещание и телевидение, медицинское приборостроение и измерительную технику, автомобильную и бытовую электронику и многое другое. Не случайно в широком спектре вопросов, затронутых системой МАТЛАБ, приложениям, упомянутым выше, уделено особое внимание.

В действительности, система МАТЛАБ это огромный мир средств и возможностей решения разнообразных задач в различных областях человеческой деятельности. Построенная по единым принципам для разных предметных областей, МАТЛАБ одновременно является и операционной средой, и языком программирования. Для упрощения, прежде всего, технических решений в системе разработаны и продолжают развиваться:

• предметно ориентированный инструментарий TOOLBOXES пакеты прикладных программ;
• SIMULINK система для имитационного моделирования проектов, представленных в виде композиции функциональных блоков, источников сигналов, приемников и измерительных средств;
• МАТЛАБ EXTANTIONS набор программных средств, позволяющий упростить и ускорить реализацию разработок, выполненных с использованием МАТЛАБ (это компилятор, библиотека функций на языке С и С++ и др.);
• GUI графический интерфейс пользователя – средство, позволяющее в предметной области для наиболее часто встречающихся задач одного плана (расчет фильтров, спектральный анализ, вейвлет-анализ и др.) создать инструмент анализа, расчета, проектирования, максимально приближенный к практическим потребностям инженера и требующий для освоения минимальных интеллектуальных и временных затрат.

По системе МАТЛАБ написано много книг (см. www.mathworks.com и библиографию к заметке), только на русском языке около 10. Упомянутые издания можно разделить на несколько групп:

• книги, посвященные собственно системе МАТЛАБ или отдельным ее частям;
• книги, посвященные организации и проведению учебного процесса по различным аспектам системы;
• книги прикладного или теоретического характера в конкретных предметных областях, использующие МАТЛАБ как инструмент для решения примеров и задач и средство организации иллюстраций.

В качестве предметной области, для которой строятся содержательные примеры, использованы приложения, имеющие дело с обработкой сигналов. А в качестве предмета обучения выбраны два типа инструментов: МАТЛАБ-SIMULINK и GRAPHICAL USER INTERFACE (GUI). Первый обеспечивает имитационное моделирование сложных систем в разнообразных режимах, а второй графический интерфейс пользователя предназначен для решения задач анализа и синтеза расчета разнообразных объектов в режиме, максимально удобном и наглядном для пользователя.

Во многих (хотя далеко не во всех) случаях именно с помощью этого инструментария инженер либо студент может решить часто встречающиеся задачи с минимальными затратами времени и сил на обучение и прийти к цели кротчайшим путем. Именно это обстоятельство способно увлечь, сформировать неформальный интерес и в последующем побудить читателя к основательному знакомству с МАТЛАБ.

Введение

Simulink является мощным средством решения таких задач для разных предметных областей и, может быть, в первую очередь, для задач в области цифровой обработки сигналов. Использование Simulink во многих случаях исключает утомительные и трудоемкие этапы составления и отладки программ, позволяя сосредоточить основные усилия непосредственно на решении "своих" предметно-ориентированных задач. Инженеру или студенту нужно освоить правила использования готовых функциональных блоков, из которых, как из конструктора, составляется модель проектируемого устройства, а также, и это следует особо подчеркнуть, "испытательный стенд", то есть вся необходимая инфраструктура, включающая источники сигналов, измерительные приборы и средства наблюдения за процессами и характеристиками процессов. При этом гарантируется высокое качество "строительного материала", в создании которого использованы опыт и знания ведущих специалистов.

Итак, Simulink – это интерактивная графическая программа, управляемая мышью, которая позволяет моделировать динамические системы на уровне структурных и функциональных схем. Библиотеки Simulink содержат большое количество разнообразных функциональных блоков, которые отображаются на экране в виде пиктограмм.

Построение модели сводится к перемещению с помощью мыши необходимых блоков из библиотек Simulink в окно создаваемой модели и соединению этих блоков между собой. Работая с программой Simulink, можно создавать модели линейных и нелинейных, аналоговых, дискретных и смешанных (аналогово-дискретных) цепей и систем, изменять параметры блоков непосредственно во время процесса моделирования и сразу же наблюдать реакцию моделируемой системы. Все это делает работу с Simulink одинаково привлекательной как для начинающих пользователей, так и для опытных специалистов. В пакет MATLAB 5.3 входит подробное описание программы Simulink, которое содержится в файле sl_using.pdf. Отметим также вышедшие недавно книги [1,2], содержащие основные сведения о Simulink и примеры моделей динамических систем.

В настоящей работе описывается процесс построения простой модели аналого-цифрового преобразователя (АЦП), а также рассматриваются эффекты, связанные с аналого-цифровым преобразованием. В первой части приводятся состав и краткое описание модели, процесс ее построения, а также процедура компоновки модели. Во второй части приведены процесс построения модели, необходимые сведения о входящих в нее функциональных блоках и результаты моделирования, а также дополнительные возможности по использованию модели.

Компоновка модели

Перед построением модели необходимо предварительно загрузить систему MATLAB и запустить Simulink. Запуск выполняется из командного окна MATLAB, для чего необходимо подвести курсор мыши к кнопке запуска этой программы, находящейся в верхней части окна, и щелкнуть левой клавишей мыши либо набрать в командном окне следующую команду simulink, как показано на рис. 2.

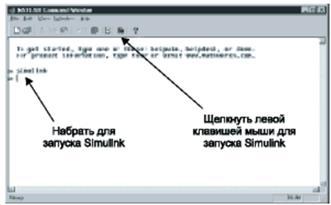
Рисунок 2. Командное окно MATLAB и запуск Simulink

В том и другом случае откроется окно Simulink Library Browser (система просмотра библиотек Simulink), изображенное на рис. 3. В верхней части этого окна две крайние левые кнопки служат, соответственно, для создания новой и открытия существующей модели. После нажатия левой кнопки на экране появится окно для построения новой модели. Процесс построения модели АЦП, как впрочем, и любой другой модели Simulink, включает ее компоновку и задание необходимых параметров. Компоновка заключается в выборе из библиотек Simulink необходимых блоков, их размещение в открывшемся окне и соединение между собой.

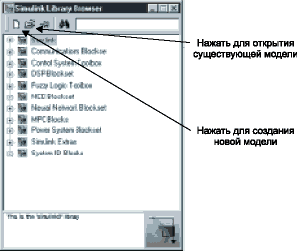
Рисунок 3. Система просмотра библиотек Simulink Library Browser

Поиск и перемещение блоков

Процедура поиска и перемещения блоков из библиотек Simulink в окно модели во многом напоминает операции копирования и перемещения файлов в среде Windows. В частности, технология работы с Simulink Library Browser (рис. 3) аналогична работе с Проводником Windows. Поместим в окно модели блоки источников сигналов Signal Generator (генератор синусоидальных, прямоугольных, пилообразных и случайных сигналов) и Band-Limited White Noise (генератор шума в заданной полосе частот), находящиеся по адресу Simu-link\Sources, для чего откроем библиотеку Simulink в окне Simulink Library Browser и находящуюся в ней библиотеку Sources. В результате, окно Simulink Library Browser примет вид, аналогичный показанному на рис. 4 (там также указаны блоки, которые следует переместить в окно модели). Для перемещения курсор мыши устанавливается на нужный блок. Затем, нажав левую клавишу мыши, блок перемещает его в окно модели. Отметим, что, кроме непосредственного просмотра содержимого библиотек, любой блок может быть найден по имени (если оно известно), введенному в текстовое поле, расположенное в правой верхней части Simulink Library Browser (рис. 4).

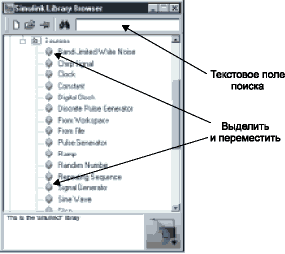
Рисунок 4. Библиотека Sources

Кроме источников сигналов нам потребуются следующие блоки, которые также следует поместить в окно модели:

• блок выборки и хранения Simulink\Discrete\Zero-OrderHold (то есть блок Zero-Order Hold, находящийся в библиотеке Simulink\Discrete)═ осуществляет выборку мгновенного значения входного сигнала в заданный момент времени и фиксацию его на выходе вплоть до следующего момента выборки;
• квантователь Simulink\Nonlinear\Quantizer выполняет квантование входного сигнала по уровню;
• сумматор Simulink\Math\Sum (пиктограмма имеет вид кружка со знаками арифметических операций "+" и/или "-") выполняет суммирование входных дискретных сигналов с учетом указанных знаков;
• коэффициент умножения Simulink\Math\Gain выполняет умножение входного сигнала на заданную величину;
• константа Simulink\Sources\Constant генерирует постоянную величину;
• ручной переключатель Simulink\Nonlinear\Manual Switch изменяет свое состояние двойным щелчком левой клавишей мыши;
• мультиплексор Simulink\Signals&Systems\Mux позволяет передавать указанное количество входных сигналов по одной линии, подключенной к выходу блока;
• осциллограф Simulink\Sinks\Scope отображает в виде графика входной сигнал;
• цифровой индикатор Simulink\Sinks\Display отображает численное значение текущего отсчета входного сигнала;
• блок вычисления дисперсии DSP Blockset\Math Functions\Statistics\Variance вычисляет дисперсию входного сигнала;
• блок вычисления гистограмм DSP Blockset\Math Functions\Statistics\Histogram вычисляет гистограмму для заданного диапазона значений входного сигнала;
• блок графического отображения DSP Blockset\DSP Sinks\User-Defined Frame Scope позволяет строить графики входных данных, не ограничивая пользователя только временными или частотными зависимостями;
• блок буферизации и вычисления квадрата преобразования Фурье DSP Blockset\DSP Sinks\Buffered FFT Frame Scope накапливает в буфере отсчеты входного сигнала, после заполнения буфера вычисляет квадрат преобразования Фурье.

Рисунок 5. Входные и выходные порты

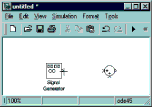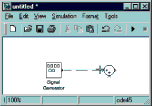Рисунок 6. Соединение блоков: а) в этом положении курсора нажать левую клавишу мыши; б) в этом положении курсора отпустить нажатую клавишу

Из рис. 1 видно, что для построения модели требуется по два блока Zero-Order Hold, Scope, Mux, Constant, Buffered FFT Frame Scope, Sum и три блока Gain. Конечно, можно многократно повторять процедуру перемещения одного и того же блока из библиотеки в окно создаваемой модели, однако Simulink позволяет создавать копии (дубликаты) блоков из имеющихся в окне модели. Для создания копии блока надо установить курсор на требуемый блок в окне модели, нажать на клавиатуре клавишу "Ctrl" и затем левую клавишу мыши. В результате, слева от курсора появится знак "+" (рис. 7а). Затем, удерживая клавиши в нажатом положении, переместить в нужное место курсор и отпустить нажатые клавиши. При построении модели, как видно из рис. 1, требуется не только соединять блоки между собой, но и делать ответвления от существующих соединительных линий. Например, линия, соединяющая блоки Quantizer и сумматор, имеет ответвление к блоку Gain1. Проведение линии, соединяющей входной порт какого-либо блока с существующей линией, выполняется аналогично дублированию блоков, то есть при нажатой клавише "Ctrl". Разница лишь в том, что в этом случае курсор мыши устанавливается на линию, от которой проводится ответвление, и перемещается к входному порту соединяемого блока, или, наоборот (от входного порта к линии).

Рисунок 7. Дублирование блоков: а) начальное положение курсора и результат нажатия левой клавиши мыши и "CTRL" на клавиатуре; б) результат перемещения курсора при удерживаемых клавишах

Задание параметров модели

Следующим шагом после построения модели простейшего АЦП является задание параметров входящих в неё блоков. Для этого надо дважды щёлкнуть левой клавишей мыши по выбранному блоку. В результате откроется окно, в котором показаны значения параметров, введённые ранее или установленные по умолчанию. В качестве примера на рис. 8 показано окно блока Signal Generator, в котором задана частота синусоидального сигнала, равная 128 Гц (по умолчанию – 1 Гц). Чтобы новые установки вступили в сипу, после ввода параметров надо щёлкнуть по кнопке "Apply" или "ОК". Окно параметров каждого блока имеет кнопку "Help" для получения необходимой справочной информации, поэтому здесь мы ограничимся рассмотрением лишь некоторых блоков, представляющих интерес с точки зрения обработки сигналов, а именно, Variance, Histogram и Buffered FFT Frame Scope. Эти блоки, как, впрочем, большинство блоков библиотеки DSP, работают как со скалярными, так и с векторными последовательностями (скалярными и векторными дискретными сигналами).

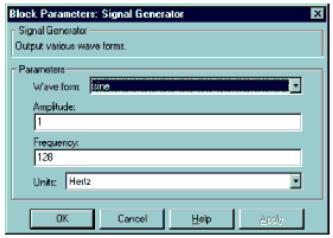
Рисунок 8. Окно и значения параметров блока Signal Generator

Примером скалярной последовательности может служить одноканальный сигнал, когда данные следуют одно за другим, то есть каждому временному отсчету соответствует одно значение сигнала. Многоканальный сигнал, когда одному и тому же временному отсчету соответствуют несколько значений, представляет собой векторную последовательность. Таким образом, скалярный сигнал задается вектором или одномерным массивом и (рис. 9а), в то время как векторный сигнал – матрицей U размерности MxN, в которой М строк соответствуют моментам времени 1, 2, ... М, а N значений k-ой строки представляют собой мгновенную выборку сигнала в момент времени к (рис. 9 б).

Окно параметров блока Variance показано на рис. 10. Блок предназначен для вычисления дисперсии входной последовательности данных и, в зависимости от параметра Running Variance, может работать в двух режимах: Basic Operation и Running Operation. Если этот параметр не включен, работа выполняется в режиме Basic Operation. В этом случае, если входная последовательность векторная, блок на каждом временном шаге вычисляет дисперсию текущей мгновенной выборки, если же входная последовательность скалярная, то, поскольку мгновенная выборка состоит из одного значения, выходом блока будет нуль.

Рисунок 9. Скалярные и векторные сигналы: а) скалярный сигнал; б) векторный сигнал

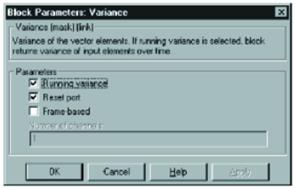
Рисунок 10. Окно и значения параметров блока Variance

В нашем случае (