Частные производные и дифференциал

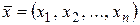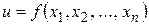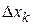
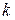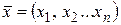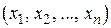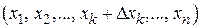Пусть точка является внутренней точкой области задания функции . Дадим приращение -й координате точки и рассмотрим разность значений функции в точках и . Приращение функции

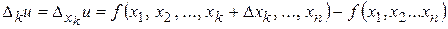
называют частным приращениемфункции 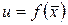в точке .

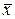Определение 15. Предел отношения частного приращения 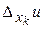функции 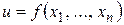к соответствующему приращению аргумента 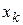при 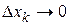(если он существует) называется частной производной функции 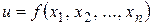в точке 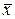по аргументу 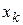и обозначается одним из следующих символов:

.

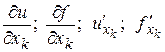Таким образом, получаем

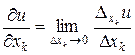. (5)

Отметим, что частная производная функция 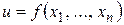по переменной 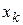представляет собой обыкновенную производную по переменной 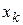при фиксированных значениях остальных переменных.

Вычисления частных производных выполняются по обычным правилам, определенным для функции одной переменной.

Примеры. 1)Найти частные производные функции .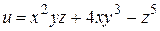

Решение. .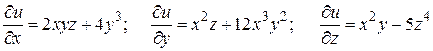

2)Найти частные производные функции .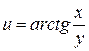

Решение. , .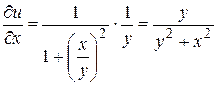

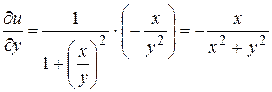Если задать приращения 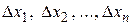по всем переменным в точке 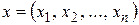, то получим полное приращение функции:

.

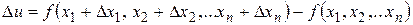
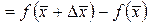Определение 16. Функция 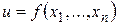называется дифференцируемойв точке 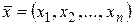, если ее полное приращение может быть представлено в виде

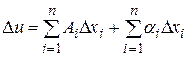. (6)

где 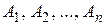некоторые не зависящие от 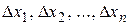числа, а 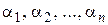бесконечно малые величины при 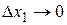, , 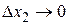…, , 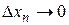т.е. .

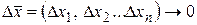Соотношение (6) называют условием дифференцируемости функции в точке 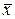. Его еще можно записать так:

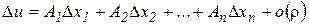, (7)

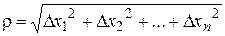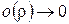где , при 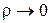. Нетрудно показать, что равенства (6) и (7) эквивалентны.

Если хотя бы одно из чисел 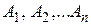отлично от 0, то сумма 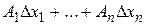называется главной, линейной относительно приращений аргументов, частью полного приращения функции. Например, для функции двух переменных 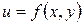приращение функции

,

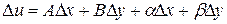а главная часть приращения .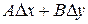

Теорема 5. Если функция 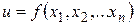дифференцируема в точке 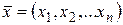, то в этой точке существуют частные производные по всем аргументам, причем 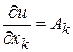, , 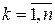где 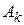определяется из условия (6) или (7) дифференцируемости функции.

ƒ Из условия (6) следует, что частное приращение по переменной 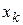будет иметь вид

.

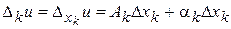Отсюда 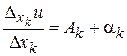, 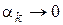при .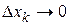

Тогда

. <

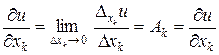Следствие 1. Условие дифференцируемости можно записать в виде

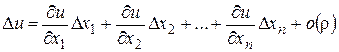. (8)

Для функции :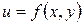

.

Следствие 2. Если 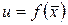дифференцируема в точке 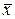, то преставление ее полного приращения 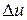в формуле (6) или (7) единственно.

Теорема 6. Если функция 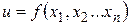дифференцируема в точке 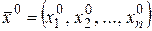, то она непрерывна в этой точке.

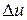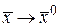ƒ Полное приращение функции имеет вид (6) или (7). Найдем предел при , где .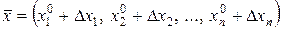

.

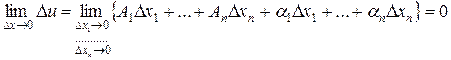Отсюда 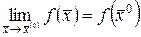. Следовательно, по определению 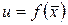непрерывная в точке <

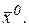Теорема 7. Если функция 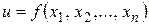имеет непрерывные частные производные по всем аргументам в некоторой окрестности точки 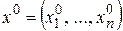, то 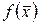дифференцируема в этой точке.

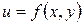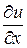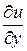ƒ Рассмотрим доказательство для функции двух переменных . Пусть существуют непрерывные и в окрестности точки 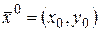. Дадим аргументам приращения 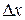и 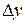. Тогда полное приращение в точке 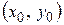можно записать так:

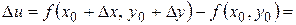(9)

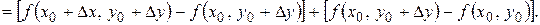
Первую скобку можно рассматривать как приращение функции по одной переменной 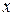. Так как функция имеет частные производные, то, используя формулу Лагранжа, получим

.

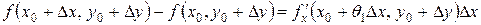Аналогично

.

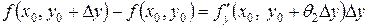Здесь 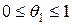и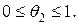

Поскольку производные 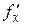и 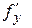непрерывные то можно записать:

,

,

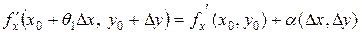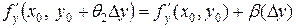где .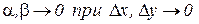

Подставляя всё это в (9) получим

.

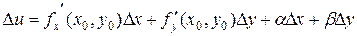А это означает, что функция 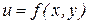дифференцируема в точке . ■

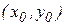Определение 17.Дифференциаломdu дифференцируемой в точке 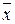функции 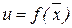называется главная, линейная относительно приращений всех аргументов, часть полного приращения функции в этой точке.

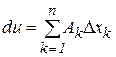
Если все коэффициенты 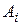в (6) или (7) дифференцируемой функции равны нулю, то и дифференциал в этой точке считается равным нулю. По теореме будем иметь:

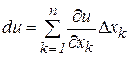(10)

В частности, для функции двух переменных получаем:

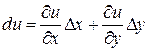
Дифференциалом независимой переменной 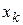будет называться число равное приращению 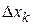, т.е. 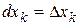. Тогда (10) можно записать в виде

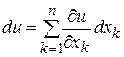. (11)

Заметим, что формула (11) справедлива, если 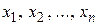независимые переменные. Но ниже будет доказано, что ее можно использовать, когда 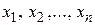являются дифференцируемыми функциями некоторых переменных.

Есл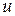и и дифференцируемые функции, то справедливы следующие соотношения, которые легко проверять по определению:

,

,

.

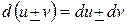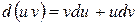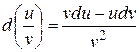Полный дифференциал применяется при приближенных вычислениях значений функции. При достаточно малом 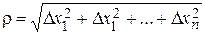имеет место приближенное равенство

,

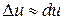или, подробно

.

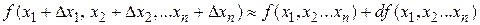Если для функции 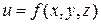известны максимальные погрешности 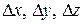значений переменных, то максимальная абсолютная погрешность 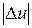при вычислении значения функции составляет

,

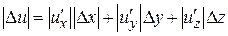а максимальная относительная погрешность равна

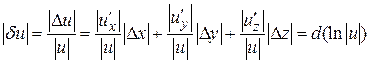
В некоторых задачах прикладного характера полезно понятие линеаризации функции. Пусть функция двух переменных 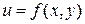дифференцируема в точке 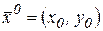, тогда

.

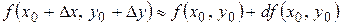Заменяя 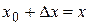, 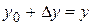получим

.

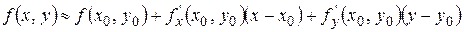В правой части этого равенства стоит линейная функция двух переменных. Замена функции 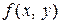в окрестности точки 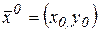линейной функцией называется её линеаризацией. Аналогично производится линеаризация функции n переменных в окрестности точки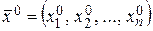

.

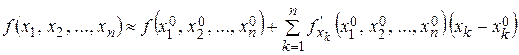Примеры.1) Найти дифференциал функции .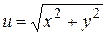

Решение. .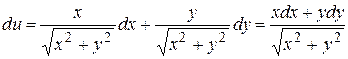

2) Вычислить приближенное 1,01^3,02 .

Решение. Рассмотрим функцию 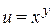. Искомое число будем рассматривать как значение функции при 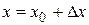, , 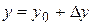где , , , .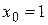

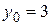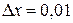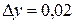Тогда

.

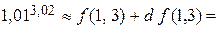
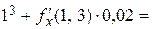
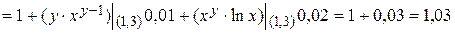3) Высота конуса 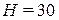см, радиусоснования 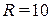см. Как изменится объем конуса, если Н увеличить на 3 мм., а 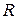уменьшить на 1 мм.

Решение. Объем конуса равен 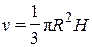. Изменение объема заменим приближенно дифференциалом

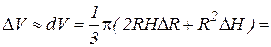
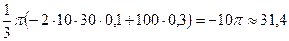см ³.