Функции нескольких переменных. Предел и непрерывность.
Определение 5. Пусть 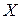 множество в
множество в 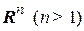 , и каждой точке
, и каждой точке 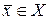 поставлено в соответствие единственное действительное число
поставлено в соответствие единственное действительное число 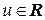 . В этом случае говорят, что на множестве Х определена числовая функция n переменных или функция нескольких переменных.
. В этом случае говорят, что на множестве Х определена числовая функция n переменных или функция нескольких переменных.
Правило, по которому устанавливается соответствие, обозначают некоторой буквой, например 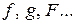 и пишут
и пишут
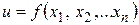 или
или 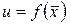 ,
, 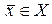 .
.
Другими словами функция n переменных есть отображение множества 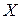 на множество
на множество 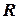 :
:
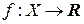 , где
, где 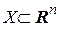 .
.
Множество Х является областью определения функции 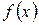 , а
, а 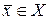 называют аргументом или независимой переменной. Функция
называют аргументом или независимой переменной. Функция 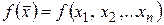 называется элементарной, если она задана с помощью конечного числа арифметической операции и суперпозиций элементарных функций одной переменной.
называется элементарной, если она задана с помощью конечного числа арифметической операции и суперпозиций элементарных функций одной переменной.
Определение 6. Графиком функции 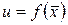 называют множество точек
называют множество точек 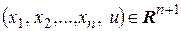 связанных соотношением
связанных соотношением 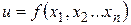 .
.
Примеры. 1) Функция 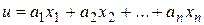 является линейной функцией n переменных и называетсягиперплоскостью. Область определения её все точки, принадлежащие
является линейной функцией n переменных и называетсягиперплоскостью. Область определения её все точки, принадлежащие 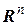 .
.
2) Функция 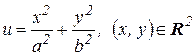 называется эллиптическим параболоидом. Если a=b, то это параболоид вращения.Область определения ее множество
называется эллиптическим параболоидом. Если a=b, то это параболоид вращения.Область определения ее множество 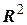 (нарисовать график).
(нарисовать график).
3) Для функции 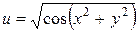 область определения получается из условия
область определения получается из условия 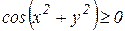 . Откуда следует, что выполнятся неравенства
. Откуда следует, что выполнятся неравенства 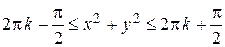 (
( 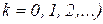 . Таким образом, областью определения являются концентрические кольца с центром в начале координат.
. Таким образом, областью определения являются концентрические кольца с центром в начале координат.
4) Функция n-переменных
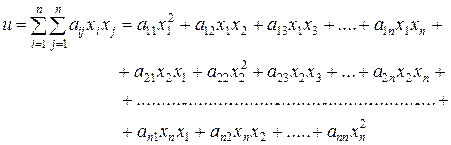
называется квадратичной формой (квадратичная функция n переменных).
Пусть  определяется на
определяется на 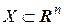 и
и 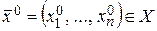 есть предельная точка множества Х.
есть предельная точка множества Х.
Определение 7 (О.Л. Коши 1789-1857 фр.). Число 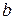 называется пределом функции
называется пределом функции  в
в 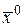 , если для любого положительного
, если для любого положительного 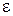 можно указать положительное число
можно указать положительное число 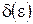 такое, что из выполнения условия
такое, что из выполнения условия 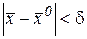 для любого
для любого 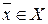 следует выполнение неравенства
следует выполнение неравенства 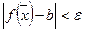 .
.
Это определение символически можно записать следующим образом:
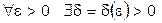
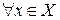 :
: 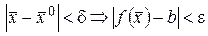 .
.
Определение 8. (Г.Э.Гейне 1821-1881 нем.). Число 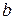 называется пределом
называется пределом в точке
в точке 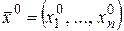 , если
, если 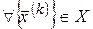 , сходящейся
, сходящейся  к
к  следует, что последовательность
следует, что последовательность 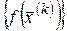 сходится к
сходится к 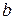 .
.
Как и для функции одной переменной доказывается, что определения 7 и 8 равносильны. Предел функции многих переменных обозначается
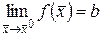 или
или 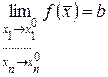 .
.
Пример. Найти 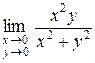 .
.
Решение. Докажем, что предел равен 0. Выберем 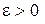 , возьмем
, возьмем 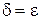 , такое, что
, такое, что 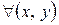 , удовлетворяющих условию
, удовлетворяющих условию 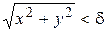 и отличных от начала координат справедливо неравенство:
и отличных от начала координат справедливо неравенство:
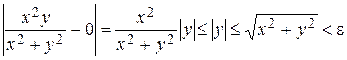 .
. 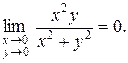
Для пределов функций нескольких переменных справедливы следующие утверждения, аналогичные соответствующим теоремам для функций одной переменной.
• Если  имеет предел при
имеет предел при  , то он единственный.
, то он единственный.
•Критерий Коши. Для того, чтобы  имела конечный предел при
имела конечный предел при 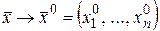 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 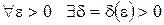 , такое что для
, такое что для 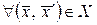 из выполнения условий
из выполнения условий 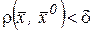 и
и 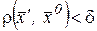 следовало бы выполнение неравенства
следовало бы выполнение неравенства 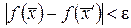 .
.
• Пусть 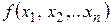 и
и 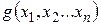 функции с общей областью определения и существуют пределы
функции с общей областью определения и существуют пределы 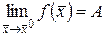 и
и 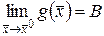 . Тогда существуют пределы функций
. Тогда существуют пределы функций 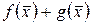 ,
, 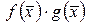 и
и 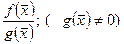 и имеют место равенства:
и имеют место равенства: 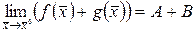 ,
, 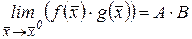 ,
, 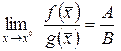 ,
, 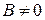 .
.
Определение 9. Число 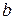 называется пределом функции
называется пределом функции при
при 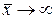 , если
, если 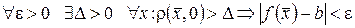 и записывается
и записывается 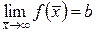 .
.
Определение 10. Пусть 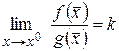 и
и 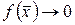 ,
, 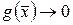 при
при 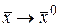 . Если
. Если 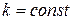 , то
, то  и
и 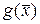 называются бесконечно малыми одного порядка при
называются бесконечно малыми одного порядка при 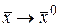 . Если
. Если 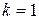 , то функции
, то функции  и
и 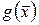 называются эквивалентными при
называются эквивалентными при 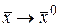 . Если
. Если 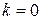 , то функция
, то функция  называется бесконечно малой более высокого порядка по отношению к
называется бесконечно малой более высокого порядка по отношению к 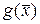 .
.
Определение 11. Число 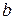 называют пределом функции
называют пределом функции 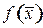 по множеству
по множеству 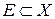 в точке
в точке , если
, если 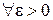
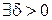 , такое что для произвольного
, такое что для произвольного 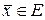 из выполнения условия
из выполнения условия 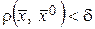 следует
следует 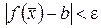 . Обозначение
. Обозначение 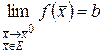 .
.
Это обобщение предела функции в точке, на тот случай, когда функция рассматривается не во всей окрестности точки  , а на некоторой ее части.
, а на некоторой ее части.
Если  есть непрерывная кривая Г, проходящая через точку
есть непрерывная кривая Г, проходящая через точку  , то
, то 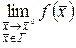 называют пределом
называют пределом  по кривой Г.
по кривой Г.
В частности, если Г – есть прямая линия с направленным единичным вектором 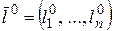 ,
, 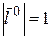 , то предел по Г называют пределом по направлению вектора
, то предел по Г называют пределом по направлению вектора 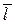 .
.
Для функции n-переменных при 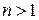 можно рассматривать n, так называемые, повторные пределы. В частности для функции двух переменных
можно рассматривать n, так называемые, повторные пределы. В частности для функции двух переменных 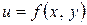 можно рассматривать два повторных предела в точке
можно рассматривать два повторных предела в точке 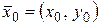 :
:
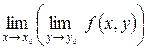 и
и 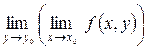 .
.
Если оба повторных предела существуют, то они не обязательно равны между собой.
Пример. Найти предел функции 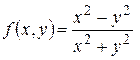 в точке
в точке 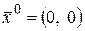 .
.
Решение. 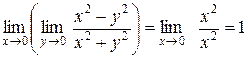 .
.
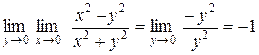 .
.
Теорема 3. Если функция 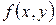 определена в
определена в 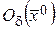 ,
, 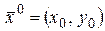 , за исключением может быть самой точки
, за исключением может быть самой точки  , существует предел
, существует предел 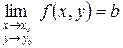 и существуют пределы
и существуют пределы 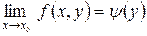
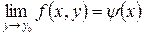 , тогда существуют и повторные пределы
, тогда существуют и повторные пределы 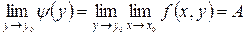 и
и 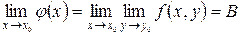 , которые равны между собой и равны
, которые равны между собой и равны 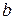 :
: 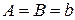 .
.
□ По определению предела функции двух переменных имеем, что 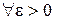 существует
существует 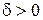 , такое что, если
, такое что, если 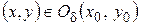 , то есть
, то есть 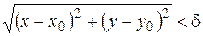 . Отсюда следует, что
. Отсюда следует, что 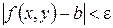 . Переходя к пределу в этих неравенствах при
. Переходя к пределу в этих неравенствах при 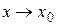 , получим, что при
, получим, что при 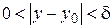 имеет место неравенство
имеет место неравенство 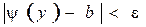 . Отсюда следует, что
. Отсюда следует, что 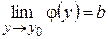 .
.
Таким образом, 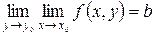 . Аналогично доказывается, что
. Аналогично доказывается, что 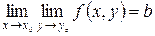 . <
. <
Пусть 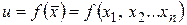 определена на
определена на 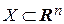 .
.
Определение 12. Функция  называют непрерывной в точке
называют непрерывной в точке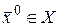 , если
, если  – предельная точка множества X;
– предельная точка множества X;  – определена в точке
– определена в точке  и
и 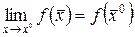 .
.
На языке « 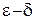 » последнее означает, что
» последнее означает, что 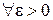
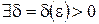 , такое, что
, такое, что 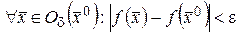 .
.
Другими словами, если 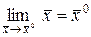 , то тогда
, то тогда
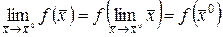 .
.
Если  не является непрерывной в точке
не является непрерывной в точке  , то она называется разрывной в этой точке, а точку
, то она называется разрывной в этой точке, а точку  называют точкой разрыва. Можно доказать, что всякая элементарная функция
называют точкой разрыва. Можно доказать, что всякая элементарная функция 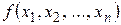 является непрерывной в каждой точке, в которой она определена.
является непрерывной в каждой точке, в которой она определена.
Примеры.1) Исследовать функцию 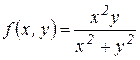 на непрерывность.
на непрерывность.
Решение. Функция всюду определена и непрерывна, кроме точки 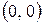 . Ранее было показано, что
. Ранее было показано, что 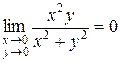 . Тогда точка (0, 0) является точкой устранимого разрыва, т.к.
. Тогда точка (0, 0) является точкой устранимого разрыва, т.к. 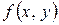 неопределенна, но предел существует и равен 0. Если доопределить
неопределенна, но предел существует и равен 0. Если доопределить 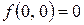 , то получим непрерывную функцию.
, то получим непрерывную функцию.
2) Исследовать функцию 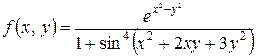 на непрерывность.
на непрерывность.
Решение. Функции 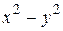 и
и 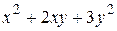 непрерывны при всех
непрерывны при всех 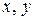 как многочлены. По теореме о непрерывности суперпозиции непрерывных функций вытекает, что
как многочлены. По теореме о непрерывности суперпозиции непрерывных функций вытекает, что 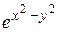 и
и 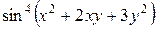 непрерывны. Так как
непрерывны. Так как 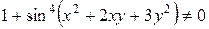 при любых значениях
при любых значениях 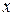 и
и 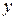 , то
, то 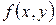 непрерывна.
непрерывна.
Определение 13. Функция 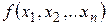 называется непрерывной намножестве
называется непрерывной намножестве 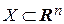 , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества.
Как и для функций одной переменной справедливы следующие утверждения.
• Если функции  и
и 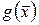 определены на множестве
определены на множестве 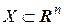 и непрерывны в точке
и непрерывны в точке 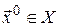 , то в
, то в  определены и непрерывны функции
определены и непрерывны функции 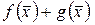 ,
, 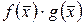 ,
, 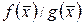
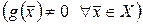 .
.
• Если  определена и непрерывна в
определена и непрерывна в 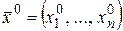 , тогда существует окрестность точки
, тогда существует окрестность точки 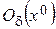 , в которой выполняется условие
, в которой выполняется условие 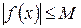 . Это означает, что функция ограничена в окрестности этой точки.
. Это означает, что функция ограничена в окрестности этой точки.
• Если  определена и непрерывна в точке
определена и непрерывна в точке  и
и 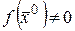 , то существует такая окрестность этой точки, в которой
, то существует такая окрестность этой точки, в которой  сохраняет знак.
сохраняет знак.
• Если функции 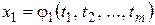 ,
, 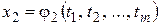 , …,
, …, 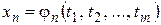 непрерывны в точке
непрерывны в точке 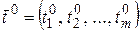 , а функция
, а функция 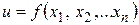 непрерывна в точке
непрерывна в точке 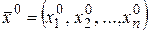 , где
, где 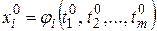 ,
, 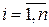 , то сложная функция
, то сложная функция 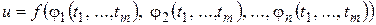 непрерывна в точке
непрерывна в точке 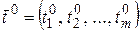 .
.
Эти теоремы доказываются так же, как теоремы для функций одной переменной.Справедлива также теорема.
Теорема 4 (Коши о прохождении непрерывной функции через любое промежуточное значение). Пусть 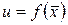 непрерывна на линейно-связанном множестве
непрерывна на линейно-связанном множестве 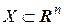 , причем
, причем 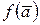 и
и 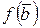 значения
значения 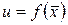 в точках
в точках 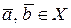 , а
, а 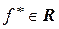 такое, что
такое, что 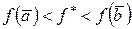 . Тогда на любой непрерывной кривой Г, соединяющей точки
. Тогда на любой непрерывной кривой Г, соединяющей точки 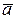 и
и 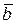 , целиком принадлежащей Х существует такая точка
, целиком принадлежащей Х существует такая точка 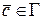 , что
, что 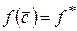 .
.
ƒ Пусть 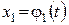 ,
, 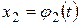 , …,
, …, 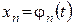 ,
, 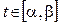 – параметрические уравнения кривой
– параметрические уравнения кривой 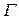 , соединяющей точки
, соединяющей точки 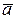 и
и 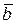 из множества
из множества 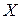 и
и 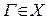 . Тогда на отрезке
. Тогда на отрезке 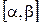 определена сложная функция одной переменной
определена сложная функция одной переменной 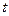
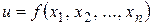 , где
, где 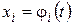 . Очевидно, значение этой функции на отрезке
. Очевидно, значение этой функции на отрезке 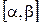 совпадают со значениями
совпадают со значениями 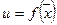 на
на 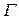 . По теореме о непрерывной сложной функции она непрерывна, а, следовательно, по теореме о прохождении промежуточных значений для функции одной переменной
. По теореме о непрерывной сложной функции она непрерывна, а, следовательно, по теореме о прохождении промежуточных значений для функции одной переменной 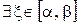 :
: 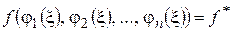 . Поэтому в точке
. Поэтому в точке 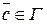 , координаты которой
, координаты которой 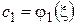 ,
, 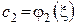 , …,
, …, 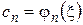 будет справедливо равенство
будет справедливо равенство 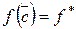 . <
. <
Определение 14. Функция 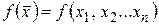 называется равномерно-непрерывной на множестве
называется равномерно-непрерывной на множестве 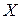 , если для любого положительного
, если для любого положительного 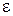 найдется такое положительное число
найдется такое положительное число 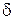 , что для
, что для 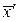 и
и 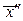 из множества Х таких, что при
из множества Х таких, что при 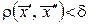 выполняется неравенство
выполняется неравенство 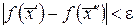 .
.
Это же определение на языке 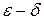 записывается следующим образом
записывается следующим образом 
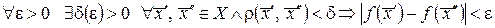 .
.
Имеют место утверждения, аналогичные теоремам для функции одной переменной.
• Если функция 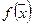 определена и непрерывна на ограниченном замкнутом множестве
определена и непрерывна на ограниченном замкнутом множестве 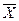 , то
, то 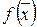 ограничена на этом множестве (первая теорема Вейерштрасса).
ограничена на этом множестве (первая теорема Вейерштрасса).
• Если функция  определена и непрерывна на ограниченном замкнутом множестве
определена и непрерывна на ограниченном замкнутом множестве 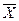 , то
, то  достигает на
достигает на 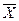 точных верхней и нижней граней, т.е.
точных верхней и нижней граней, т.е. 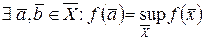
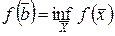 (вторая теорема Вейерштрасса).
(вторая теорема Вейерштрасса).
• Если функция  определена и непрерывна на ограниченном замкнутом множестве
определена и непрерывна на ограниченном замкнутом множестве 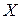 , то
, то  равномерно непрерывна на множестве
равномерно непрерывна на множестве 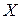 (теорема Кантора).
(теорема Кантора).
