Глава 7. Функции нескольких переменных
Дифференцирование сложных функций
Пусть для функции n - переменных 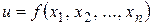 аргументы являются также функциями переменных
аргументы являются также функциями переменных 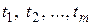 :
:
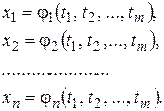 (12)
(12)
Справедлива следующая теорема о дифференцировании сложной функции.
Теорема 8. Если функции 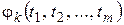 дифференцируемы в точке
дифференцируемы в точке 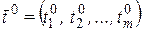 , а функция
, а функция 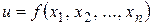 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке 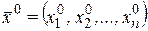 , где
, где 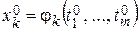 ,
, 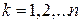 . Тогда сложная функция
. Тогда сложная функция 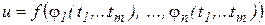 дифференцируема в точке
дифференцируема в точке 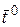 , причем частные производные определяются по формулам
, причем частные производные определяются по формулам
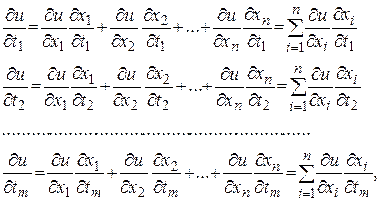
где частные производные 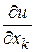 вычисляются в точке
вычисляются в точке 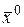 , а
, а 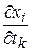 вычисляются в точке
вычисляются в точке 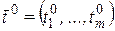 .
.
ƒ Докажем эту теорему для функции двух переменных. Пусть 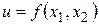 , а
, а 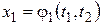
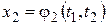 .
.
Пусть 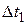 и
и 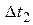 произвольные приращения аргументов
произвольные приращения аргументов 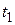 и
и 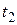 в точке
в точке 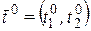 . Им соответствуют приращения
. Им соответствуют приращения 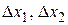 функций
функций 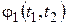 и
и 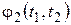 в точке
в точке 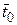 . Приращениям
. Приращениям 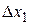 и
и 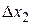 соответствует приращение
соответствует приращение 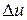 функции
функции 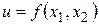 в точке
в точке 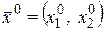 . Так как
. Так как 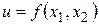 дифференцируема в точке
дифференцируема в точке 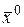 , то ее приращение может быть записано в виде
, то ее приращение может быть записано в виде
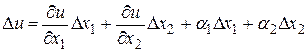 , (13)
, (13)
где 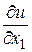 и
и 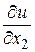 вычисляются в точке
вычисляются в точке 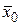 ,
, 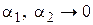 при
при 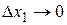 и
и 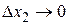 . В силу дифференцируемости функций
. В силу дифференцируемости функций 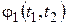 и
и 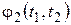 в точке
в точке 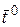 , получаем
, получаем
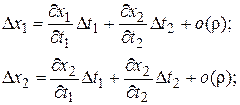 (14)
(14)
где 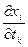 вычисляется в точке
вычисляется в точке 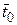 ;
; 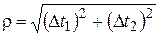 .
.
Подставим (14) в (13) и перегруппируем слагаемые
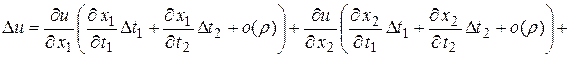
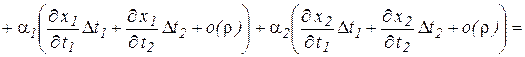
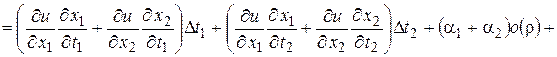
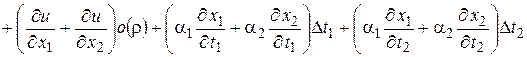 .
.
Заметим, что 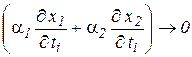 при
при 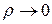 , так как
, так как 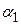 и
и 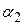 стремятся к нулю при
стремятся к нулю при 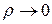 . Это следует из того, что
. Это следует из того, что 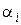 бесконечно малые при
бесконечно малые при 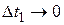 и
и 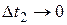 . Но функции
. Но функции 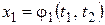 и
и 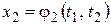 дифференцируемы, а, следовательно, и непрерывны в точке
дифференцируемы, а, следовательно, и непрерывны в точке 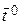 . Поэтому если
. Поэтому если 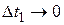 и
и 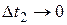 , то
, то 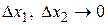 . Тогда
. Тогда 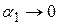 и
и 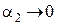 при
при 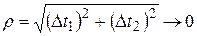 .
.
Так как частные производные вычисляются в точке 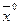 , то получаем
, то получаем
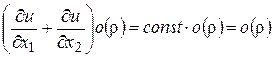 .
.
Обозначим
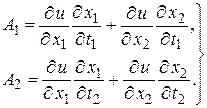 (15)
(15)
Тогда
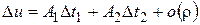 ,
,
а это и означает, что 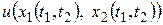 дифференцируема по переменным
дифференцируема по переменным 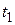 и
и 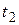 , причем
, причем
 и
и 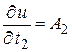 . <
. <
Следствие. Если 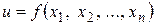 , причем
, причем 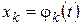 ,
, 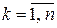 , т.е.
, т.е. 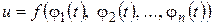 , то производная по переменной t вычисляется по формуле
, то производная по переменной t вычисляется по формуле
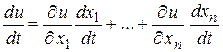 .
.
Если 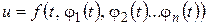 , то
, то
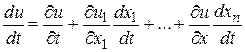 .
.
Последнее выражение называетсяформулой полной производной для функции многих переменных.
Примеры. 1) Найти полную производную функции 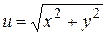 , где
, где 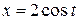 ,
, 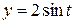 .
.
Решение. 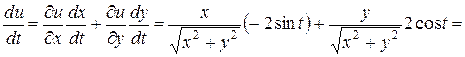
= 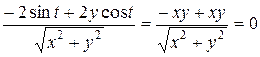 .
.
2) Найти полную производную функции 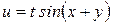 , если
, если 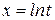 ,
, 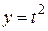 .
.
Решение.
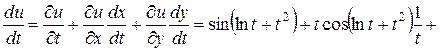
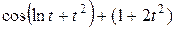 .
.
Используя правила дифференцирования сложной функции, получим одно важное свойство дифференциала функции многих переменных.
Если 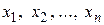 независимые переменные функции
независимые переменные функции 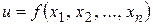 , то дифференциал по определению равен:
, то дифференциал по определению равен:
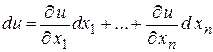 . (16)
. (16)
Пусть теперь аргументы 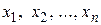 есть дифференцируемые функции в некоторой точке функции
есть дифференцируемые функции в некоторой точке функции 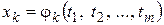 по переменным
по переменным 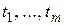 , а функция
, а функция 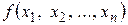 дифференцируема по переменным
дифференцируема по переменным 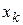 ,
, 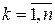 . Тогда
. Тогда 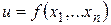 можно рассматривать как сложную функцию переменных
можно рассматривать как сложную функцию переменных 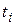 ,
, 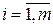 . Она по предыдущей теореме дифференцируема и имеет место соотношение
. Она по предыдущей теореме дифференцируема и имеет место соотношение
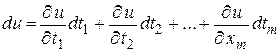 , (17)
, (17)
где 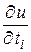 определяется по формулам (12). Подставим (12) в (17) и, собирая коэффициенты при
определяется по формулам (12). Подставим (12) в (17) и, собирая коэффициенты при 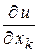 , получим
, получим
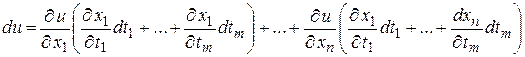 .
.
Поскольку коэффициент при производной 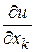 равен дифференциалу
равен дифференциалу 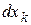 функции
функции 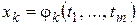 , то для дифференциала сложной функции получили снова формулу (16).
, то для дифференциала сложной функции получили снова формулу (16).
Таким образом, формула первого дифференциала не зависит от того, являются ли ее аргументы функциями, или они независимыми. Это свойство называют инвариантностью формы первого дифференциала.
Глава 7. Функции нескольких переменных
7.1. Пространство Rn. Множества в линейном пространстве.
Множество, элементами которого являются всевозможные упорядоченные наборы из n действительных чисел 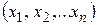 , обозначается
, обозначается 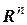 и называется n-мерным арифметическим пространством,а числоn называется размерностью пространства. Элемент
и называется n-мерным арифметическим пространством,а числоn называется размерностью пространства. Элемент 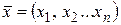 множества
множества 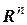 называется точкой пространства, или вектором, а числа
называется точкой пространства, или вектором, а числа 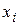 координатами этой точки. Точка
координатами этой точки. Точка 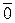 =(0, 0, …0) называется нулевой или началом координат.
=(0, 0, …0) называется нулевой или началом координат.
Пространство 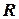 – есть множество действительных чисел, т.е.
– есть множество действительных чисел, т.е. 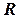 – числовая прямая;
– числовая прямая; 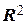 и
и 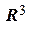 – есть двумерная координатная геометрическая плоскость и трехмерное координатное геометрическое пространство соответственно. Векторы
– есть двумерная координатная геометрическая плоскость и трехмерное координатное геометрическое пространство соответственно. Векторы 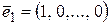 ,
, 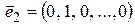 , …,
, …, 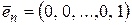 называются единичным базисом.
называются единичным базисом.
Для двух элементов 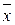 ,
, 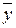 множества
множества 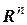 определяются понятия суммы элементов и произведения элемента на действительное число:
определяются понятия суммы элементов и произведения элемента на действительное число:
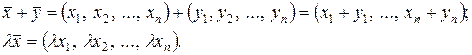
Очевидно, что 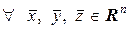 и
и 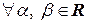 в силу этого определения и свойств действительных чисел справедливы равенства:
в силу этого определения и свойств действительных чисел справедливы равенства:
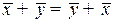 ;
;
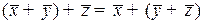 ;
;
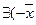 )
) 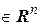 :
: 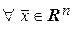 :
: 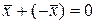 ;
;
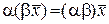 ;
;
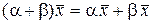
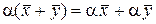 .
.
Согласно этим свойствам, пространство 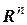 называется также линейным (векторным) пространством.
называется также линейным (векторным) пространством.
В линейном пространстве 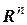 определяется скалярное произведение элементов
определяется скалярное произведение элементов 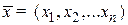 и
и 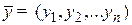 как действительное число, вычисляемое по следующему правилу:
как действительное число, вычисляемое по следующему правилу:
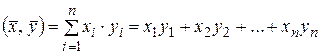 , (1)
, (1)
Число 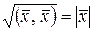 называется длиной вектора
называется длиной вектора 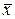 или нормой
или нормой 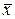 . Векторы
. Векторы 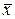 и
и 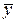 называются ортогональными, если
называются ортогональными, если 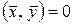 . Величина
. Величина
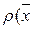 ,
, 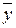 )= │
)= │ 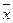 -
- 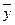 │ =
│ = 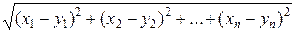
называется расстоянием между элементами 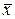 и
и 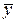 .
.
Если 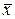 и
и 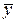 ненулевые векторы, то углом между ними называется угол
ненулевые векторы, то углом между ними называется угол 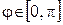 , такой, что
, такой, что
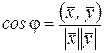 .
.
Легко убедиться, что для любых элементов 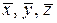 и действительного числа
и действительного числа 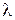 , выполняются скалярного произведения:
, выполняются скалярного произведения:
1) 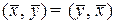 ;
;
2) 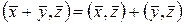 ;
;
3) 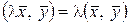 ;
;
4) 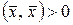 , при
, при 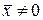 .
.
Линейное пространство 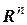 с определенным в нем по формуле (1) скалярным произведением называется евклидовым пространством.
с определенным в нем по формуле (1) скалярным произведением называется евклидовым пространством.
Пусть точка 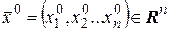 и
и 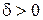 . Множество всех точек
. Множество всех точек 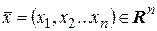 для которых выполняются неравенства
для которых выполняются неравенства
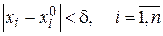 ,
,
называется n-мерным кубом с ребром 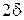 и с центром в точке
и с центром в точке 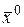 . Например, двумерный куб есть квадрат со стороной
. Например, двумерный куб есть квадрат со стороной 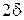 с центром в точке
с центром в точке 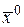 .
.
Множество точек 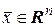 , удовлетворяющих неравенству
, удовлетворяющих неравенству 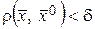 , называются n-мерным шаром радиуса
, называются n-мерным шаром радиуса 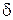 с центром в точке
с центром в точке 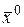 , который также называют
, который также называют
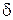 -окрестностью точки
-окрестностью точки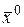 в
в 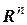 и обозначают
и обозначают 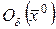 ,
,
т.е.
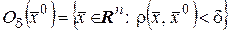 .
.
Таким образом, одномерный шар 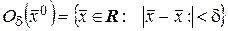 есть интервал длиной
есть интервал длиной 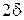 . Двумерный шар
. Двумерный шар
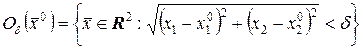
есть круг, для которого выполняется неравенство
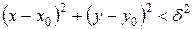 .
.
Определение 1. Множество 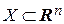 называется ограниченным, если существует
называется ограниченным, если существует
n - мерный шар, содержащий это множество.
Определение 2. Функция, заданная на множестве натуральных чисел и принимающая значения, принадлежащие 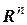 , называется последовательностью в пространстве
, называется последовательностью в пространстве 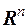 и обозначается
и обозначается 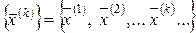 , где
, где 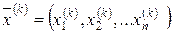 .
.
Определение 3. Точка 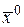 называется пределом последовательности
называется пределом последовательности 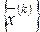 , если для произвольного положительного числа
, если для произвольного положительного числа 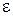 существует натуральное число
существует натуральное число 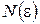 , такое что для любого числа
, такое что для любого числа 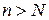 выполняется неравенство
выполняется неравенство 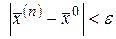 .
.
Символически это определение записывается следующим образом:
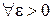
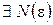
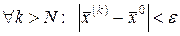 .
.
Обозначение:
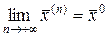 .
.
Из определения 3 следует, что 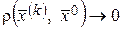 , при
, при 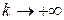 . Такая последовательность называется сходящейся к
. Такая последовательность называется сходящейся к 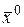 .
.
Если последовательность не является сходящейся ни к одной точке, то она называется расходящейся.
Теорема 1. Для того чтобы последовательность 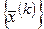 сходилась к точке
сходилась к точке 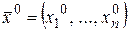 необходимо и достаточно, чтобы для любого номера
необходимо и достаточно, чтобы для любого номера 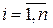 выполнялось
выполнялось 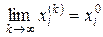 , т.е. чтобы последовательность i - х координат точек
, т.е. чтобы последовательность i - х координат точек 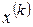 сходилась к i - й координате точки
сходилась к i - й координате точки 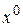 .
.
□ Доказательствоследует из неравенств
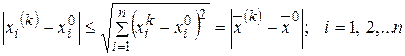 . <
. <
Последовательность 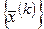 называется ограниченной, если множество её значений ограничено, т.е.
называется ограниченной, если множество её значений ограничено, т.е.
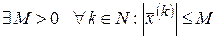 .
.
Как и числовая последовательность, сходящаяся последовательность точек 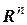 ограничена и имеет единственный предел.
ограничена и имеет единственный предел.
Определение 4. Последовательность 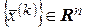 называется фундаментальной (последовательностью Коши), если для любого положительного числа
называется фундаментальной (последовательностью Коши), если для любого положительного числа 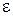 можно указать такое натуральное число
можно указать такое натуральное число 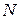 , что для произвольных натуральных чисел
, что для произвольных натуральных чисел 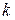 и
и 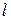 , больших
, больших 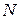 , выполняется
, выполняется 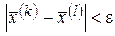 , т.е.
, т.е.
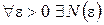
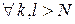 :
: 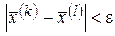 .
.
Теорема 2 (критерий Коши). Для того чтобы последовательность 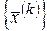 была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.
была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.
□ Необходимость. Пусть 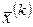 сходится к точке
сходится к точке 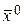 . Тогда
. Тогда 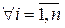 получаем последовательность
получаем последовательность 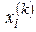 , сходящуюся к
, сходящуюся к 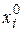 .
.
В силу критерия Коши для действительных чисел каждая из этих числовых последовательностей фундаментальная. Отсюда для любого произвольного положительного числа 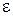 найдется
найдется 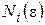 такое, что для произвольных положительных
такое, что для произвольных положительных 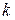 и
и 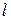 , больших, чем
, больших, чем 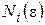 , выполнится
, выполнится 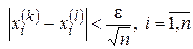 . Обозначим
. Обозначим 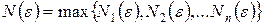 . Тогда при
. Тогда при 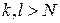 имеет место неравенство
имеет место неравенство
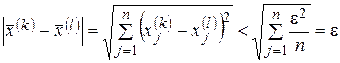 .
.
А это означает, что последовательность фундаментальная.
Достаточность. Пусть 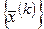 – фундаментальная последовательность. Тогда из неравенств
– фундаментальная последовательность. Тогда из неравенств
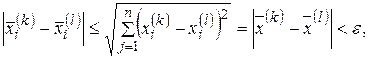
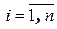
следует, что каждая из числовых последовательностей 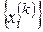 фундаментальна. В силу критерия Коши для действительных чисел каждая из этих последовательностей сходится:
фундаментальна. В силу критерия Коши для действительных чисел каждая из этих последовательностей сходится: 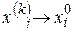 . Следовательно, по теореме 1 последовательность
. Следовательно, по теореме 1 последовательность 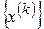 сходится. <
сходится. <
В пространстве 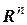 существуют различные типы точек и множеств.
существуют различные типы точек и множеств.
• Точка множества 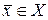 называется внутренней точкой этого множества, если существует
называется внутренней точкой этого множества, если существует 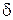 - окрестность
- окрестность 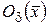 содержащаяся в X:
содержащаяся в X: 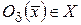 .
.
• Множество, каждая точка которого является его внутренней точкой, называется открытым множеством в 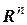 . Понятно, что пространство
. Понятно, что пространство 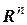 является открытым множеством.
является открытым множеством.
• Точка 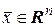 называется точкой прикосновения множества X, если любая окрестность этой точки содержит хотя бы одну точку множества Х.
называется точкой прикосновения множества X, если любая окрестность этой точки содержит хотя бы одну точку множества Х.
• Точка 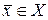 называется изолированной точкой множества Х, если существует окрестность этой точки, не содержащая других точек множества Х, отличных от
называется изолированной точкой множества Х, если существует окрестность этой точки, не содержащая других точек множества Х, отличных от 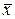 .
.
• Точка 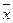 называется предельной точкоймножества Х, если в любой её окрестности содержится хотя бы одна точка множества, отличная от
называется предельной точкоймножества Х, если в любой её окрестности содержится хотя бы одна точка множества, отличная от 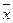 .
.
• Точка 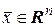 называется граничной точкой множества Х, если любая ее окрестность содержит как точку, принадлежащую множеству Х, так и точку, не принадлежащую множеству Х.
называется граничной точкой множества Х, если любая ее окрестность содержит как точку, принадлежащую множеству Х, так и точку, не принадлежащую множеству Х.
Все граничные точки множества Х называются границей множества Х и обозначают 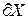 .
.
Пример.Для множества 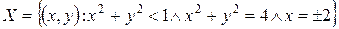 определить внутренние, предельные, изолированные и граничные точки, а также точки прикосновения.
определить внутренние, предельные, изолированные и граничные точки, а также точки прикосновения.
Решение. Внутренние точки – все точки круга. Точки прикосновения – все точки множества. Изолированная точки 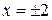 . Предельные точки – точки множества
. Предельные точки – точки множества 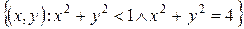 . Граничные точки – точки, удовлетворяющие уравнениям:
. Граничные точки – точки, удовлетворяющие уравнениям: 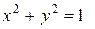 ,
, 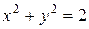 и
и 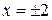 .
.
• Множество Х называется замкнутым, если оно содержит все свои точки прикосновения. Множество всех точек прикосновения называют замыканием множества Х и обозначают 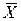 .
.
• Если 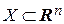 и
и 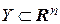 , то число
, то число 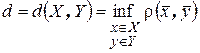 называют расстоянием между множествами X и Y. Диаметром множества Х называют число
называют расстоянием между множествами X и Y. Диаметром множества Х называют число 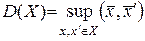 .
.
• Непрерывной кривой Г в 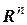 называется множество точек
называется множество точек 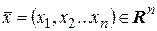 , координаты которых есть непрерывные функции параметра
, координаты которых есть непрерывные функции параметра 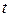 , заданного на отрезке
, заданного на отрезке 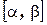 , т.е.
, т.е. 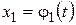 ,
, 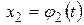 , …,
, …, 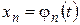 , где
, где 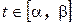 . Число
. Число 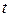 называют параметром, а сами уравнения
называют параметром, а сами уравнения 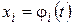 параметрическими уравнениями кривой.
параметрическими уравнениями кривой.
Например, система уравнений 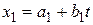 ,
, 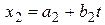 , …,
, …, 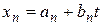 при
при 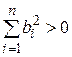 и
и 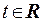 задает прямую в
задает прямую в 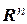 . Если
. Если 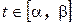 , то эта система задает отрезок прямой.
, то эта система задает отрезок прямой.
• Множество 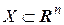 называют линейно-связанным, если любые две его точки можно соединить непрерывной кривой, принадлежащей этому множеству. Линейно-связанное открытое множество Х называют областью в
называют линейно-связанным, если любые две его точки можно соединить непрерывной кривой, принадлежащей этому множеству. Линейно-связанное открытое множество Х называют областью в 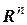 . Если Х – область, то ее замыкание
. Если Х – область, то ее замыкание 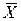 называют замкнутой областью.
называют замкнутой областью.
• Множества X и Y называют отделимыми, если ни одно из них не содержит точек прикосновения другого.
• Множество Х называют связанным, если оно не может быть представлено в виде объединения двух отделимых множеств.
• Множество Х называют выпуклым, если любые его две точки можно соединить отрезком, целиком принадлежащим этому множеству.
Пример. Опираясь на сформулированные выше определения, можно утверждать, что
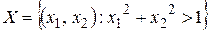 – связанное, линейно-связанное, открытое, невыпуклое множество, является областью.
– связанное, линейно-связанное, открытое, невыпуклое множество, является областью.
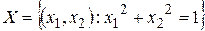 – связанное, линейно-связанное, неоткрытое, невыпуклое множество, не является областью.
– связанное, линейно-связанное, неоткрытое, невыпуклое множество, не является областью.
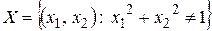 – несвязанное, не линейно-связанное, открытое, невыпуклое множество, не является областью.
– несвязанное, не линейно-связанное, открытое, невыпуклое множество, не является областью.
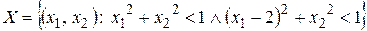 – несвязанное, не линейно-связанное, открытое множество, не является областью.
– несвязанное, не линейно-связанное, открытое множество, не является областью.
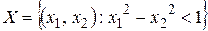 – связанное, линейно-связанное, открытое множество, является областью.
– связанное, линейно-связанное, открытое множество, является областью.
