Матричная форма записи задачи межотраслевого баланса Леонтьева и ее решение. Условие разрешимости балансовых уравнений

Рассмотрим модель межотраслевого баланса, называемую еще моделью Леонтьева, или моделью «затраты – выпуск». Предположим, что производственный сектор народного хозяйства разбит на n отраслей (энергетика, машиностроение, сельское хозяйство и т. д.).

Рассмотрим отрасль 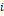, 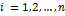. Она выпускает некую продукцию за данный промежуток времени (например, за год) в объеме 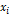, которое ещё называют валовым выпуском. Часть объема продукции 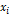, произведенная 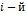отраслью, используется для собственного производства в объеме 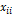, часть –поступает в остальные отрасли 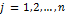для потребления при производстве в объемах 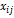, и некоторая часть объемом 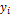– для потребления в

непроизводственной сфере, так называемый объем конечного потребления.

Перечисленные сферы распределения валового продукта 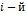отрасли приводят к соотношению баланса

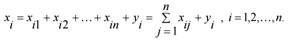
Введем коэффициенты прямых затрат 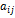, которые показывают, сколько единиц продукции i-й отрасли затрачивается на производство одной единицы продукции в отрасли j. Тогда можно записать, что количество продукции, произведенной в отрасли i в объеме 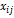и поступающей для производственных нужд в отрасль j, равно .

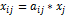Считаем сложившуюся технологию производства во всех отраслях неизменной (за рассматриваемый период времени), означающей, что коэффициенты прямых затрат 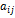постоянны. Тогда получаем следующее соотношение баланса, называемого моделью Леонтьева:

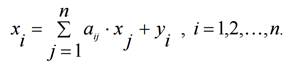
Введем вектор валового выпуска 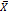, матрицу прямых затрат A и вектор конечного потребления :

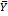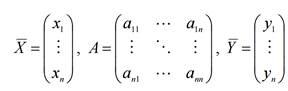
Модель Леонтьева можно записать в матричном виде:

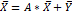
Матрица A ≥ 0, у которой все элементы 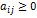(неотрицательны), называется продуктивной матрицей, если существует такой неотрицательный вектор .

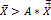Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт .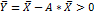

Модель Леонтьева с продуктивной матрицей A называется продуктивной моделью.

Для проверки продуктивности матрицы A достаточно существования обратной матрицы 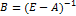с неотрицательными элементами, где матрица E – единичная матрица:

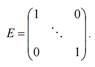
С помощью модели Леонтьева можно выполнить три вида плановых расчетов, при условии соблюдения условия продуктивности матрицы A:

1. Зная (или задавая) объемы валовой продукции всех отраслей 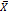, можно определить объемы конечной продукции всех отраслей .

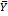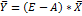
2. Задавая величины конечной продукции всех отраслей 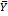, можно определить величины валовой продукции каждой отрасли

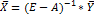
3. Задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

Матрица 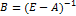называется матрицей полных материальных затрат. Ее смысл следует из матричного равенства, которое можно записать в виде .

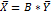Элементы матрицы B показывают, сколько всего необходимо произвести продукции в i-ой отрасли, для выпуска в сферу конечного потребления единицы продукции отрасли j.

Пример MathCAD:

Задана модель экономики, в которой выделены четыре сектора: три производящих сектора (промышленность, сельское хозяйство, транспорт) и домашние хозяйства в качестве сектора конечного спроса. Структура экономики описана в таблице межотраслевого баланса (объемы указаны в единицах стоимости):

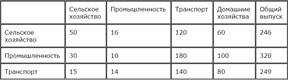
Вычислить вектор выпуска для вектора конечного спроса Y=(100 150 120).

1. Переменная ORIGIN содержит номер первой строки (столбца) матрицы или первого элемента вектора. По умолчанию ORIGIN:=0. Обычно же в математической записи используется нумерация с 1, поэтому определяем значение этой переменной равным 1.

ORIGIN:=1

2. Это матрица межотраслевого баланса, элементами которой являются количество товаров и услуг i-го сектора, потребляемое j-им сектором (i=1,2,3;j=1,2,3,4). Смотрите таблицу межотраслевого баланса.

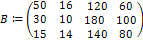
3. Первоначальный вектор выпуска, заданный в таблице (общий выпуск).

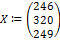
4. Построение структурной матрицы А по формуле 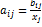- количество продукции i-го сектора, которое расходуется при производстве одной единицы продукции j-го сектора (коэффициенты прямых затрат).

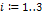
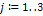
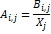
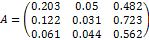
5. Построение матрицы полных затрат по формуле 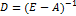, где единичная матрица 3-го порядка Е=identity(3) - встроенная функция MathCAD.

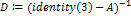
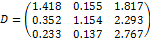
6. Новый вектор конечного спроса

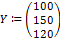
7. Вычисление вектора выпуска при новом векторе конечного спроса по формуле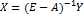

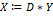
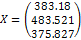
Итак, при векторе конечного спроса Y=(100 150 120) вектор выпуска X=(383.18 483.521 375.827).