Обзор современных компьютерных систем для решения экономико-математических задач

Обзор современных компьютерных систем для решения экономико-математических задач

На рынке современных математических систем в настоящее время присутствует целый ряд крупных фирм: Macsyma, Inc., Waterloo Maple Software, Inc., Wolfram Research, Inc., MathWorks, Inc., MathSoft, Inc., SciFace GmbH и др.

MATLAB — продукт компании MathWorks, Inc.(http://www.mathwork.com/), представляющий собой язык высокого уровня для научно-технических вычислений. Среди основных областей применения MATLAB — математические расчеты, разработка алгоритмов, моделирование, анализ данных и визуализация, научная и инженерная графика, разработка приложений, включая графический интерфейс пользователя. MATLAB решает множество компьютерных задач — от сбора и анализа данных до разработки готовых приложений. Среда MATLAB соединяет в себе математические вычисления, визуализацию и мощный технический язык. Встроенные универсальные интерфейсы позволяют легко работать с внешними информационными источниками, а также осуществлять интеграцию с процедурами, написанными на языках высокого уровня (C, C++, Java и др.).

MathCAD — Это интегрированная среда для выполнения, документирования и обмена результатами технических вычислений от компании MathSoft, Inc. (http://www.mathsoft.com/). Данный продукт позволяет пользователям вводить, редактировать и решать уравнения, визуализировать результаты, документировать их, а также обмениваться результатами анализа, отслеживая при этом их размерность.

Maple — продукт компании Waterloo Maple Software, Inc. (http://www.maplesoft.com/) часто называют системой символьных вычислений или системой компьютерной алгебры. Maple позволяет выполнять как численные, так и аналитические расчеты с возможностью редактирования текста и формул на рабочем листе.

Mathematica

Система Mathematica — компании Wolfram Research, Inc. (http://www.wolfram.com/) имеет чрезвычайно широкий набор средств, переводящих сложные математические алгоритмы в программы. По сути дела, все алгоритмы, содержащиеся в курсе высшей математики технического вуза, заложены в память компьютерной системы Mathematica.

Mathematica имеет мощный графический пакет, с помощью которого можно строить графики очень сложных функций одной и двух переменных.

Macsyma

Macsyma от компании Macsyma, Inc. (http://www.macsyma.com/) — это одна из первых математических программ, оперирующих символьной математикой. Сильные стороны Macsyma — развитой аппарат линейной алгебры и дифференциальных уравнений. Система ориентирована на прикладные расчеты и не предназначена для теоретических исследований в области математики. В связи с этим в программе отсутствуют или сокращены разделы, связанные с теоретическими методами (теория чисел, теория групп, и др.).

MuPAD

MuPAD является программным пакетом компьютерной алгебры, предназначенным для решения математических задач различного уровня сложности. Основные качественные отличия MuPAD — невысокие требования к ресурсам PC, наличие собственного ядра символьной математики, способность к развитию самим пользователем и мощные средства визуализации решения математических задач.

S-PLUS

S-PLUS представляет собой интерактивную компьютерную среду, обеспечивающую полнофункциональный графический анализ данных и включающую оригинальный объектно-ориентированный язык. Гибкая система S-PLUS может использоваться для исследовательского анализа данных, статистического анализа и математических вычислений, а также для удобного графического представления анализируемых данных.

2 – Программирование в MathCAD: операторы, примеры использования

Рассмотрим все команды из панели программирования Mathcad.

1. Add Line – добавить строку в текущую позицию программы. При вводе данной команды появляется или расширяется на одну строку вертикальная линия, объединяющая отдельные операторы в блок с одним входом и одним выходом, который выполняется как один оператор. Для того чтобы начать ввод подпрограммы, необходимо набрать имя программы и в скобках через запятую перечислить формальные параметры подпрограммы, ввести нужное количество раз команду Add Line. Программа выводит последнюю переменную, обрабатываемую программой перед выходом. Вместо имени подпрограммы можно указать имя переменной, куда необходимо вывести результат работы подпрограммы.

2. Оператор присваивания. В Mathcad имеются два оператора присваивания: для глобальных переменных (обозначается двумя символами «:=») и для локальных переменных «←». Глобальные переменные доступны в любом месте программы после объявления данной переменной, а локальные – только в текущем блоке.

Напишем программу для решения квадратного уравнения ax2+bx+c=0. В программе при помощи операторов глобального присваивания задаются значения глобальных переменных a, b и c. Для сравнения введем еще локальную переменную k и присвоим ей значение 4. Далее вычисляем значение корней квадратного уравнения при помощи программы, состоящей из одного блока операторов. В программе применяются три оператора локального присваивания и возвращается значения вектора x, состоящего из двух чисел. После выполнения программы выводим значение всех переменных, используемых в программе. При этом значение всех локальных переменных D, x и k, заданных вне блока, программа не видит, поэтому вместо знака = выводится оператор глобального присваивания «:=». В этом случае значение переменной не выводится, а вместо него отображается красный прямоугольный маркер.

3. Оператор if предназначен для организации разветвляющихся вычислительных процессов.

Общий вид простого оператора if: D if L, L – логическое выражение; D – оператор, выполняемый в случае, если условие L принимает значение «истина».

Оператор работает следующим образом:

• вычисляется логическое условие L;

• если L – истина, то выполняется оператор D, в ином случае он не выполняется;

• выполнение программы продолжается со следующего, после if, оператора.

Для формирования сложных условий можно использовать панель инструментов Boolean, содержатся знаки логического равенства, неравенства и логических операций. В частности, «V» означает логическое «или», а «Λ» — логическое «и».

Таким образом, чтобы сформулировать условие, что переменная х находится в диапазоне (–3;4), необходимо написать: x > –3 Λ x < 4.

В сложных подпрограммах часто используется блочный оператор if:

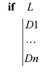
Где D1, …, Dn – действия, выполняемые в случае, если логическое условие L истинно.

Пример:

4. Оператор otherwise применяется в случае, когда используется условие с двумя вариантами действия, то есть, если условие истинно, нужно выполнить одно действие (или действия), а если ложно, то другое.

Общий вид такого оператора следующий:

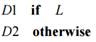
Рассмотрим пример программы, использующей операторы if и otherwise. В данном случае проверяются условия, при которых логарифм не существует (x<0 или y<0 или y=1). Если они выпол-нены, выдается сообщение «error», в противном случае вычисляется x.

5. Оператор for используется для создания циклических вычислительных процессов.

Где i – счетчик цикла. Переменная, которая меняется в диапазоне от k1 до kn. Диапазон изменения счетчика цикла вводится с помощью ранжированной переменной или с помощью вектора. D –действия, которые выполняются в цикле (тело цикла).

Приведём пример, в котором диапазон изменения счетчика цикла n задан с помощью вектора. Вектор вставляется с помощью панели инструментов Matrix.

Данная программа вычисляет сумму

Sum=1+1/2+1/5+1/7+1/10+1/11+1/13+1/16+1/17+1/19.

6. Оператор цикла while используется тогда, когда цикл должен выполняться не заданное количество раз, а до тех пор, пока не будет выполнено определенное в цикле условие.

где L – условие, при выполнении которого выполняется цикл (условие цикла). В данном случае, действие D (тело цикла) выполняется до тех пор, пока условие L истинно. Если логическое условие L изначально ложно, то операторы, составляющие тело цикла, не будут выполняться, а управление передается на оператор следующий за оператором while.

Приведем пример программы, использующей цикл while.

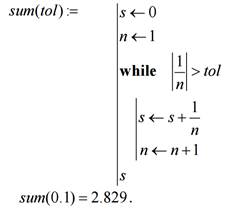
В данной программе с указанной точностью (tol) вычисляется сумма s=1+1/2+1/3+1/4+1/5+1/6+1/7…

7. Оператор break обеспечивает экстренный выход из цикла. Программа при этом продолжает выполнять следующую после цикла строку. Данный оператор часто применяется, чтобы избежать «зацикливания» программы.

В качестве примера применения оператора break рассмотрим задачу вычисления суммы числового ряда

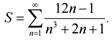В приведенной ниже программе, суммирование членов ряда прекращается, когда достигается точность, указанная параметром tol или если число итераций цикла превышает 10000.

В данном случае оператор break исключается возможность зацикливания программы для расходящегося ряда.

8. Оператор continue возвращает управление в первую строку цикла. Как только этот оператор встречается в программе, выполнение текущей итерации прерывается и выполняется переход на следующую итерацию цикла. Выход из цикла не производится.

Данный оператор, как и оператор break, не содержит параметров.

Пример: Найти сумму N первых членов ряда: 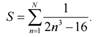В программе, при помощи оператора continue, происходит обход слагаемого в котором знаменатель дроби равен нулю.

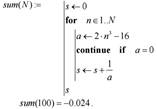
9. Оператор return прерывает выполнение программы. В качестве результата работы программы возвращается значение, указанное в позиции для ввода, после оператора return.

Пример. Подсчитать с указанной точностью tol сумму ряда: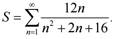

Если ряд получается расходящийся, программа выдаст сообщение «расходится». Ряд будет считаться расходящимся, если число итераций цикла превысило 1000000 раз.

10. Оператор on error отвечает за обработку ошибок. При выборе данного оператора в программу вставляется заготовка следующего вида: Общий вид оператора on error: D1 on error D2.

Если при вычислении выражения D1 произошла ошибка, будет вычислено значение D2. Данный оператор имеет смысл использовать, если при выполнении программы возможна ошибка в каком-то определенном месте, например деление на ноль. Приведем пример программы, вычисляющей десятичный логарифм числа xy. Если логарифм не существует, выдается сообщение об ошибке: «аргумент логарифма <0».

Решение задачи ЛП в MathCAD

В Mathcad к классу задач линейного программирования относятся задачи, в которых требуется оптимизировать (определить максимум или минимум) целевую функцию вида:

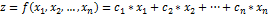
при следующих ограничениях:

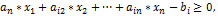
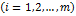
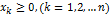
Одним из способов решение подобных задач в Mathcad является использование блока given с функциями minimize и maximize .

Функции Minimize и Maximize, которые могут быть использованы как сами по себе, так и совместно с блоком given. Аргументы функций: имя функции, экстремум которой ищется, и список ее аргументов.

- Minimize (y,x) - для отыскания значения х, соответствующего локальному минимуму функции у(х);

- Maximize (y,x) - для отыскания значения х, соответствующего локальному максимуму функции у(х).

Так как у(х) может иметь несколько локальных экстремумов, а функции Minimize (y,x) и Maximize (y,x) позволяет найти только одно значение, то в Mathcad дополнительно задается начальное приближение переменной х. В результате находится значение экстремума функции y(x), ближайшее к заданному начальному приближению переменной х.

В качестве примера рассмотрим задачу планирования производства красок.

Суть задачи в следующем. Фабрика выпускает два типа красок - I и Е. Для производства красок используются два компонента - А и В. Максимальные суточные запасы этих компонентов: компонент А - 6 тонн; компонент В – 8 тонн. Расходы компонентов А и В на производство 1 тонны краски следующие: для краски I - A/B= 2/1; для краски Е - А/В = 1/2. Суточный спрос на краску I никогда не превышает спрос на краску Е более, чем на 1 тонну. Спрос на краску I никогда не превышает 2 тонн в сутки. Оптовые цены на краску I – 2000 рублей за тонну, а на краску Е – 3000 рублей за тонну. Определить максимальный доход фабрики от продажи краски. Обозначив суточный объем выпуска краски I за x1, а суточный объем выпуска краски Е за х2, получаем экономико - математическую модель задачи, вид которой представлен ниже:

Решение задачи ЛП в MatLAB

В среде MATLAB задачи линейного программирования решаются с помощью функции linprog.

Функция linprog решает задачу линейного программирования в форме:

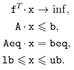
Основными входными данными linprog являются: вектор коэффициентов целевой функции f, матрица ограничений-неравенств A, вектор правых частей ограничений-неравенств b, матрица ограничений-равенств Aeq, вектор правых частей ограничений-равенств beq, вектор lb, ограничивающий план x снизу, вектор ub, ограничивающий план x сверху. На выходе функция linprog даёт оптимальный план x задачи (1) и экстремальное значение целевой функции fval.

Пример: Решим в MATLAB задачу линейного программирования:

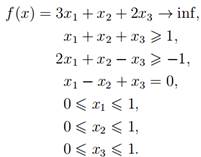
Соответствующая программа (m-файл)∗ выглядит так:

clear all

close all

clc % удаляются все текущие переменные из памяти MATLAB, закрываются все графические окна, очищается экран консоли

C = [3 1 2]; % задаётся вектор длины три

D = [1 1 1; 2 1 -1]; % строки матрицы разделяются точкой с запятой

B = [1 -1];

Aeq = [1 -1 1];

beq = [0];

lb = zeros(3,1); % задаётся нулевой вектор длины три

ub = [1 1 1];

f = C;

A = -D;

b = -B; % появляются знаки «-», так как ограничения-неравенства

Dx > B приводятся к виду −Dx 6 −B

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub);

x

fval

Запустив программу, получим сообщение

Optimization terminated.

x =

0.5000

0.5000

fval =

1.5000

Дополнительно можно задать начальное приближение x0:

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub,x0).

Если какой-то из входных параметров отсутствует, на его место следует поставить квадратные скобки [], за исключением случая, когда это последний параметр в списке. Например, если нужно решить задачу без ограничений-равенств, в которой не задано начальное приближение, то оператор вызова функции linprog будет выглядеть так: [x,fval] = linprog(f,A,b,[],[],lb,ub).

(Квадратные скобки в конце списка, соответствующие начальному приближению, не ставятся.) С помощью входного параметра options устанавливаются некоторые дополнительные настройки, в частности, выбирается алгоритм решения. MATLAB решает задачи линейного программирования двумя способами: алгоритмом внутренней точки (Large-Scale Algorithm) и вариантом симплекс-метода (Medium-Scale Algorithm). По умолчанию используется алгоритм внутренней точки. Чтобы выбрать симплекс-метод, нужно написать options = optimset(’LargeScale’,’off’,’Simplex’,’on’);

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub,[],options).

MATLAB позволяет выводить информацию о том, как завершилось решение задачи. За это отвечает параметр exitflag. Если значение exitflag равно 1, то найдено решение задачи, если равно 0, то превышено допустимое число итераций, если равно −2 — множество планов задачи пусто, если равно −3 — целевая функция не ограничена снизу на множестве планов. Интерпретация других значений параметра exitflag приведена в MATLAB Help. Для симплекс-метода допустимое число итераций (MaxIter) по умолчанию в 10 раз больше количества переменных. Значение MaxIter можно изменить. Чтобы установить допустимое число итераций равным, к примеру, 10, нужно написать

options =

optimset(’LargeScale’,’off’,’Simplex’,’on’,’MaxIter’,10);

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub,[],options).

Если после выполнения десятой итерации решение не будет найдено, параметр exitflag станет нулевым и на экране появится сообщение

Maximum number of iterations exceeded;

increase options.MaxIter.

Параметр output содержит информацию о процессе оптимизации, в частности, число итераций (iterations) и используемый алгоритм (algorithm).

Другие поля параметра output описаны в MATLAB Help. Запустим с данными из примера 1 следующую программу:

options = optimset(’LargeScale’,’off’,’Simplex’,’on’);

[x,fval,exitflag,output] =

linprog(f,A,b,Aeq,beq,lb,ub,[],options);

exitflag

output.iterations

output.algorithm

На выходе получим:

Optimization terminated.

exitflag =

ans =

ans =

medium scale: simplex

Это означает, что симплекс-метод успешно завершил работу, для нахождения решения потребовалось одна итерация. Наконец, в выходном параметре lambda содержится решение двойственной задачи линейного программирования. Параметр lambda состоит из четырёх массивов: lambda.ineqlin, lambda.eqlin, lambda.upper, lambda.lower. В этих массивах находятся двойственные переменные, приписанные ограничениям-неравенствам, ограничениям-равенствам, ограничениям на план сверху и снизу соответственно.

Пример: Решим в MATLAB задачу линейного программирования:

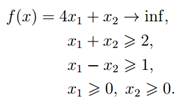
Соответствующая программа будет выглядеть так:

clear all

close all

clc

C = [4 1];

D = [1 1; 1 -1];

B = [2 1];

lb = zeros(2,1);

f = C;

A = -D;

b = -B;

options = optimset(’LargeScale’,’off’,’Simplex’,’on’)};

[x,fval,exitflag] = linprog(f,A,b,[],[],lb,[],[],options);

x

fval

exitflag

В результате работы программы получим:

Optimization terminated.

x =

1.5000

0.5000

fval =

6.5000

exitflag =

Теоретическая часть.

Межотраслевой баланс в экономике – это метод анализа взаимосвязей между различными секторами экономической системы.

Предположим, что исследуемую экономическую систему можно разделить на не- сколько отраслей, производящих определённые товары и услуги. При производстве товаров и услуг в каждой отрасли расходуются определённые ресурсы, которые производятся как в других отраслях, так и в данной отрасли. Это означает, что каждая отрасль экономики вы- ступает в системе межотраслевых связей одновременно производителем и потребителем.

Цель балансового анализа – определить, сколько продукции должна произвести каждая отрасль для того, чтобы удовлетворить все потребности экономической системы в его продукции.

Рассмотрим открытую систему межотраслевых связей, в которой вся произведенная продукция (совокупный продукт) разделяется на две части: одна часть продукции (промежуточный продукт) идёт на потребление в производящих отраслях, а другая её часть (конечный продукт) потребляется вне сферы материального производства – в секторе конечного спроса; при этом потребление в секторе конечного спроса может меняться.

Обозначим:

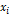- объём выпуска i-го сектора (объем товаров и услуг, произведенных в одном из n производящих секторов), i=1,2,...,n;

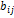- объём товаров и услуг i-го сектора, потребляемых в j-ом секторе;

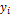- конечный продукт i-го сектора (объём продукции i-го сектора, потребляемой в секторе конечного спроса);

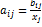- количество продукции i-го сектора, которое расходуется при производстве одной единицы продукции j-го сектора (коэффициенты прямых затрат).

Межотраслевой баланс - это равенство объема выпуска каждого производящего сек- тора суммарному объёму его продукции, потребляемой производственными секторами и сектором конечного спроса. В приведенных обозначениях имеем соотношения баланса:

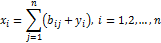
Соотношения баланса, записанные через коэффициенты прямых затрат, имеют вид:

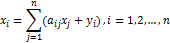
или, что то же самое,

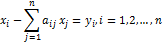
Последние равенства описывают технологию производства и структуру экономических связей и означают, что в сектор конечного спроса от каждого производственного сектора поступает та часть произведенной продукции, которая остаётся после того, как обеспечены потребности производящих секторов.

Если обозначить вектор выпуска через X, вектор спроса (вектор конечного продукта) – через Y, а структурную матрицу экономики – матрицу, элементами которой являются коэффициенты прямых затрат 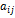– через A, то соотношение баланса в матричной форме имеют вид: (E-A)X=Y, где E – единичная матрица.

Одна из основных задач межотраслевого баланса – найти при заданной структурной матрице А экономической системы в условиях баланса совокупный выпуск X, необходимый для удовлетворения заданного спроса Y.

Если матрица обратима, то решение такой задачи определяется как 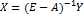. Матрица 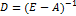называется матрицей полных затрат.

Практическая часть.

Пусть задана модель экономики, в которой выделены четыре сектора: три производящих сектора (промышленность, сельское хозяйство, транспорт) и домашние хозяйства в качестве сектора конечного спроса. Структура экономики описана в таблице межотраслевого баланса (объёмы указаны в единицах стоимости):

Вычислим вектор выпуска для вектора конечного спроса Y=(100 150 120).

Решение задачи:

ORIGIN:=1 {Переменная ORIGIN содержит номер первой строки (столбца) матрицы или первого элемента вектора. По умолчанию ORIGIN:=0. Обычно же в математической записи используется нумерация с 1, поэтому определяем значение этой переменной равным 1.}

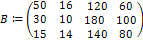{Это матрица межотраслевого баланса, элементами которой являются количество товаров и услуг i-го сектора, потребляемое j-им сектором (i=1,2,3;j=1,2,3,4). Смотрите таблицу межотраслевого баланса.}

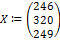{Первоначальный вектор выпуска, заданный в таблице (общий выпуск).}

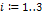
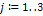
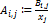{Построение структурной матрицы формуле 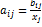- количество продукции i-го сектора, которое расходуется при производстве одной единицы продукции j-го сектора (коэффициенты прямых затрат).}

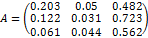
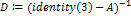
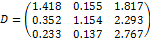{Построение матрицы полных затрат по формуле 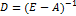, где единичная матрица 3-го порядка E=identity(3) – встроенная функция MathCAD. identity(n) n x n единичная матрица (матрица, все диагональные элементы которой равны 1, а все остальные элементы равны 0).}

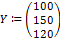{Новый вектор конечного спроса}

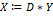
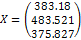{Вычисление вектора выпуска при новом векторе конечного спроса по формуле }

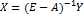Таким образом, при векторе конечного спроса 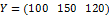вектор выпуска равен .

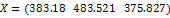Полиномиальная регрессия

Одна из наиболее известных аппроксимаций — полиномиальная. В системе MATLAB определены функции аппроксимации данных полиномами по методу наименьших квадратов — полиномиальной регрессии. Это выполняет функция, приведенная ниже:

polyfit(x.y.n) — возвращает вектор коэффициентов полинома р(х) степени п, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию у(х). Результатом является вектор-строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней х и у равно n+1, то реализуется обычная полиномиальная аппроксимация, при которой график полинома точно проходит через узловые точки с координатами (х.у), хранящиеся в векторах х и у. В противном случае точного совпадения графика с узловыми точками не наблюдается;

[p.S] = polyflt(x.y.n) — возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предсказания погрешности;

[p.S] = polyf1t(x,y,n,mu) возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предска-зния погрешности, но так, что присходит центрирование (нормирование) и масштабирование х, xnorm = (х - mu(l))/mu(2), где mu(l) = mean(x) и mu(2) = std(x). Центрирование и масштабирование не только улучшают свойства степенного многочлена, получаемого при помощи polyval, но и значительно повышают качественные характеристики самого алгоритма аппроксимации.

Пример MATLAB:

Пример (полиномиальная регрессия для функции s

» х=(-3:0.2:3)';

y=sin(x);

p=polyflt(x,y,3)

р =

-0.0953 0.0000 0.8651 -0.0000

»x=(-4:0.2:4)';y=sin(x);

» f=polyval(p,x);plot(x,y,'o',x,f)

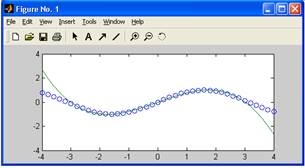
Рисунок построенный в этом примере, дает наглядное представление о точности полиномиальной аппроксимации. Следует помнить, что она достаточно точна в небольших окрестностях от точки х = 0, но может иметь большие погрешности за их пределами или в промежутках между узловыми точками.

График аппроксимирующего полинома третьей степени на рисунке показан сплошной линией, а точки исходной зависимости обозначены кружками.

Управление вычислительным процессом в MatLAB. Примеры

Для организации вычислительного процесса, который записывается в виде некоторого текста программы, необходимы операторы управления.

При этом к операторам управления вычислительным процессом обычно относят операторы безусловного перехода, условных переходов (разветвления вычислительного процесса) и операторы организации циклических процессов. Однако система MATLAB построена таким образом, что эти операторы могут быть использованы и при работе MATLAB в режиме калькулятора.

Оператор условного перехода

Конструкция оператора перехода по условию в общем, виде такова:

if <условие>

<операторы 1>

else

<операторы 2>

end

Работает он следующим образом. Вначале проверяется, выполняется

ли указанное условие. Если да, то программа выполняет совокупность опе-

раторов, которая записана в разделе <операторы 1>. В противном случае

выполняется последовательность операторов раздела <операторы 2>.

Укороченная форма условного оператора имеет вид:

if <условие>

<операторы>

end

Действие оператора в этом случае аналогично, за исключением того, что при невыполнении заданного условия выполняется оператор, следующий за оператором end.

качестве условия используется выражение типа:

<имя переменной 1> <операция сравнения> <имя переменной 2>

Операции сравнения в языке MATLAB могут быть такими:

< меньше;

> больше;

<= меньше или равно;

>= больше или равно;

= равно;

~= не равно.

Условие может быть составным, т.е. складываться из нескольких

простых условий, объединяемых знаками логических операций. Знаками

логических операций в языке MATLAB являются:

& - логическая операция И (AND);

| - логическая операция ИЛИ (OR);

~ - логическая операция НЕТ (NOT).

Логическая операция Исключающее ИЛИ может быть реализована

при помощи функции хог(А,В), где А и В - некоторые условия.

Допустима еще одна конструкция оператора условного перехода.

if <условие 1>

<операторы 1>

elseif <условие 2>

<операторы 2>

elseif <условие З>

<операторы З>

…..

else

<операторы>

end

Оператор elseif выполняется тогда, когда <условие 1> не выполнено. При этом сначала проверяется <условие 2>. Если оно выполнено, выполняются <операторы 2>, если же нет, то <операторы 2> игнорируются и происходит переход к следующему оператору elseif, т.е. к проверке <условия З>. Аналогичным образом при его выполнении обрабатываются <операторы З>, в противном случае происходит переход к следующему оператору elseif. Если ни одно из условий в операторах elseif не выполнено, обрабатываются <операторы>, следующие за оператором else. Таким образом может быть обеспечено ветвление программы по нескольким направлениям.

Пример:

function ifdem(a)

% пример использования структуры if-elseif-else

if (a ==0)

disp('a - ноль')

elseif a==1

disp('a - единица')

elseif a>=2

disp('a - двойка или больше')

else

disp('a меньше двух, но не ноль и не единица')

end

Оператор переключения

Оператор переключения имеет такую структуру:

switch <выражение, скаляр или строка символов>

сазе <значение 1>

<операторы 1>

сазе <значение 2>

<операторы 2>

….

otherwise

<операторы>

end

Он осуществляет ветвление вычислений в зависимости от значений некоторой переменной или выражения, сравнивая значение полученное в результате вычисления выражения в строке switch, со значениями, указанными в строках со словом case. Соответствующая группа операторов case выполняется, если значение выражения совпадает со значением, указанным в соответствующей строке case. Если значение выражения не совпадает ни с одним из значении в группах case, выполняются операторы, следующие за otherwise.

Пример:

function switchdem(a)

% пример использования оператора switch switch a

case 3 disp('Март')

case 4 disp('Апрель')

case 5 disp('Май')

case {1, 2, 6, 7, 8, 9, 10, 11, 12} disp('Не весенние месяцы')

otherwise

disp('Ошибка задания')

end

Операторы цикла

В языке MATLAB есть две разновидности операторов цикла - услов-

ный и арифметический.

Оператор цикла с предусловием имеет вид:

while <условие>

<операторы>

end

Операторы внутри цикла обрабатываются лишь в том случае, если выполнено условие, записанное после слова while. При этом среди операторов внутри цикла обязательно должны быть такие, которые изменяют значения одной из переменных, указанных в условии цикла.

Приведем пример вычисления значения синуса при 5 значениях аргумента от 0,2 до 1 с шагом 0,2:

Обратите внимание на то, какими средствами в приведенном примере обеспечен вывод на экран нескольких переменных в одну строку.

Для этого, используется оператор disp. Но, в соответствии с правилами применения этого оператора, в нем должен быть только один аргумент (текст, переменная или матрица). Чтобы обойти это препятствие, нужно несколько числовых переменных объединить в единый объект - векторстроку, а последнее легко выполняется при помощи обычной операции формирования вектора-строки из отдельных элементов.

[х1, х2, . . ., хN]

Таким образом, с помощью оператора вида:

disp([xl, x2, ..., xN])

можно обеспечить вывод результатов вычислений в виде таблицы данных.

Арифметический оператор цикла имеет вид:

for <Имя> = <НЗ>:<Ш>:<КЗ>

<операторы>

End

где <Имя> - имя управляющей переменной цикла - счетчика цикла; <НЗ> - заданное начальное значение этой переменной; <Ш> - значение шага, с которым она должна изменяться; <КЗ> - конечное значение переменной цикла. В этом случае <операторы> внутри цикла выполняются несколько раз (каждый раз при новом значении управляющей переменной) до тех пор, пока значение управляющей переменной не выйдет за пределы интервала между <НЗ> и <КЗ>. Если параметр <Ш> не указан, по умолчанию его значение принимается равным единице.

Чтобы досрочно выйти из цикла (например, при выполнении некоторого условия), применяют оператор break. Если в программе встречается этот оператор, выполнение цикла досрочно прекращается и начинает выполняться следующий после слова end оператор.

Для примера используем предыдущее задание:

Функции функций

Некоторые важные универсальные процедуры в MATLAB используют в качестве переменного параметра имя функции, с которой они оперируют, и потому требуют при обращении к ним указания имени М-файла, в котором записан текст программы вычисления некоторой другой процедуры (функции). Такие процедуры называют функциями функций.

Чтобы воспользоваться такой функцией от функции, необходимо, чтобы пользователь предварительно создал М-файл, в котором вычислялось бы значение нужной функции по заданному значению ее аргумента. Перечислим некоторые из стандартных функций от функций, предусмотренных в MATLAB.

Вычисление интеграла методом квадратур осуществляется процедурой:

[I, cnt] = quad('<Имя функции>', a,b)

Здесь а и b - нижняя и верхняя границы изменения аргумента функции; I - полученное значение интеграла; cn- число обращений к вычислению функции, представленной М-файлом с названием, указанным в <Имя функции>. Функция quad использует квадратурные формулы Ньютона-Котеса четвертого порядка. Аналогичная процедура quad8 использует более точные формулы 8-го порядка. Интегрирование обыкновенных дифференциальных уравнений осуществляют функции ode23 и ode45. Они могут применяться как для решения простых дифференциальных уравнений, так и для моделирования сложных динамических систем.

Известно, что любая система обыкновенных дифференциальных уравнений (ОДУ) может быть представлена в так называемой форме Коши.

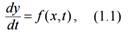
где у - вектор переменных состояния системы; t - аргумент (обычно время);

f - нелинейная вектор-функция от переменных состояния у и аргумента t.

Обращение к процедурам численного интегрирования ОДУ имеет вид:

[t, у] = оdе23('<Имя функции>', tspan, y0, options)

[t, у] = оdе45('<Имя функции>', tspan, y0, options),

где <Имя функции> - строка символов, являющаяся именем М-файла, в котором вычисляется вектор-функция f(y,t), т.е. правые части системы ОДУ;

у0 - вектор начальных значений переменных состояния;

t - массив значений аргумента, соответствующих шагам интегрирования;

у - матрица проинтегрированных значений фазовых переменных, в которой каждый столбец соответствует одной из переменных состояния, а строка содержит значения переменных состояния, соответствующих определенному шагу интегрирования;

tspan - вектор-строка [t0 tfinal], содержащая два значения. t0 – начальное значение аргумента t;

tfinal - конечное значение аргумента, options - строка параметров, определяющих значения допустимой относительной и абсолютной погрешности интегрирования.

Параметр options можно не указывать. Тогда по умолчанию допустимая относительная погрешность интегрирования принимается равной 1.0е-3, а абсолютная (по каждой из переменных состояния) - 1.0е-6. Если же эти значения не устраивают пользователя, то следует перед обращением к процедуре численного интегрирования установить новые значения допустимых погрешностей с помощью процедуры odeset таким образом:

орtions = odeset('RelTol',le-4, 'AbsTol', [le-4 le-4 le-5]).

Параметр RelTol определяет относительную погрешность численного интегрирования по всем переменным одновременно, а AbsTol является вектором-строкой, состоящим из абсолютных допустимых погрешностей численного интегрирования по каждой из фазовых переменных.

Функция ode23 осуществляет интегрирование численным методом Рунге-Кутта 2-го порядка, а с помощью метода 3-го порядка контролирует относительные и абсолютные ошибки интегрирования на каждом шаге и изменяет величину шага интегрирования так, чт