Цилиндрическая система координат.

Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:

Итого:

Билет № 26. Сферическая система координат.

Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

Для представления тройного интеграла в сферических координатах вычисляем Якобиан:

Окончательно получаем:

Билет 27 _Геометрические приложения кратных интегралов

Двойной интеграл.

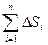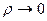1. Площадь плоской области.Из формулы 7.1 следует, что при f(x,y) ≡ 0 предел интегральной суммы при равен площади области интегрирования S, то есть 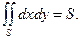(1)

2. Объем цилиндроида.Рассмотрим тело, ограниченное частью поверхности S ( z = f(x,y) ), ограниченной контуром L, проекцией этой поверхности на плоскость Оху и отрезками, параллель-ными оси Оz и соединяющими каждую точку контура L с соответствующей точкой плоскости Оху. Такое тело будем называть цилиндроидом. Тогда из формул (7.1) и (7.2) получим, что объем этого тела равен двойному интегралу от функции f(x,y) по области S: 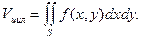(2)

3. Площадь криволинейной поверхности.Вычислим площадь части криволинейной поверхности S, заданной уравнением z = f(x,y), ограниченной контуром L. Вспомним еще раз (см. лекцию 12), что площадь элемента поверхности ΔS_i равна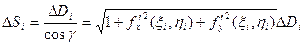

где ΔD_i – проекция ΔS_i на плоскость Оху, γ – угол между осью Оz и нормалью к ΔS_i в некоторой ее точке 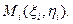Составив интегральную сумму

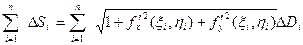
и устремив ее к пределу при 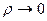, получим формулу для площади поверхности:

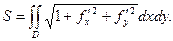
Тройной интеграл.

Объем тела.

Из определения 7.3 следует, что при f(x, y, z) ≡ 1 тройной интеграл по некоторой замкнутой области V равен объему тела V:

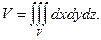(1)

Масса тела.

Если γ = γ (x, y, z) – функция, задающая плотность вещества, из которого состоит тело V, то масса тела выражается формулой

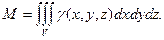(2)

Билет 28 Механические приложения кратных интегралов

Двойной интеграл

Момент инерции плоской фигуры.Вспомним определение момента инерции

а) материальной точки М с массой т относительно точки О: I = mr² (r – расстояние от М до О);

б) системы материальных точек m₁, m₂,…, m_n относительно точки О: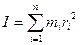

Определим теперь момент инерции относительно точки О материальной плоской фигуры D.

у

ΔS_i D

η_i P_i

r_i

O ξ_i x

Рис. 1.

Найдем момент инерции фигуры D (рис.1) относительно начала координат, считая, что плотность в каждой точке равна 1. Разобьем область D на части ΔS_i (i = 1, 2,… n) и выберем в каждой части точку P_i (ξ_i, η_i). Назовем элементарным моментом инерции площадки ΔS_i выражение вида ΔI_i = (ξ_i² + η_i²)ΔS_i и составим интегральную сумму

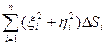(1)

для функции f(x, y) = x² + y² по области D.

О:.Предел интегральной суммы (14.4) при 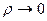называется моментом инерции фигуры D относительно начала координат:

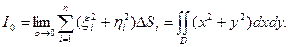(2)

О:.Интегралы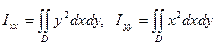

(3)

называются моментами инерции фигуры D относительно осей Ох и Оу.

Замечание. Если поверхностная плотность не равна 1, а является некоторой функци-ей γ = γ(х, у), то момент инерции фигуры относительно начала координат вычисляет-ся по формуле 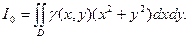(4)

Координаты центра масс плоской фигуры.

Как известно, координаты центра масс системы материальных точек P₁, P₂,…, P_n с масса-ми т₁, т₂,…, т_п определяются по формулам

.

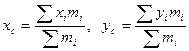Если разбить плоскую фигуру D с поверхностной плотностью, равной 1, на части, то масса каждой части будет равна ее площади. Будем считать теперь, что вся масса эле-ментарной площадки ΔS_i сосредоточена в какой-либо ее точке P_i (ξ_i, η_i). Тогда фигуру D можно рассматривать как систему материальных точек, центр масс которой определяется равенствами

.

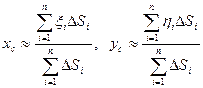Переходя к пределу при 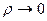, получим точные формулы для координат центра масс плоской фигуры:

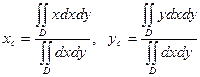. (5)

В случае переменной поверхностной плотности γ = γ (х, у) эти формулы примут вид

.

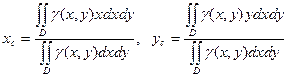Тройной интеграл

1. Момент инерции тела.

Используя формулы для моментов инерции точки М(x, y, z) массы т относительно координатных осей:

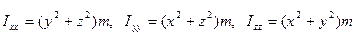
и проводя те же рассуждения, что и при определении моментов плоской фигуры, можно задать моменты инерции тела относительно координатных осей в виде:

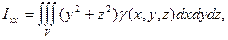
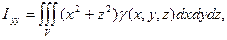(6)

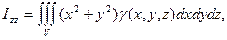
где γ (х, y, z) – плотность вещества.

2. Координаты центра масс тела.

Формулы для координат центра масс тела тоже задаются аналогично случаю плоской фигуры:

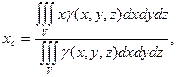
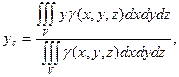
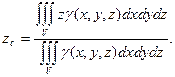(7)

Билет № 29. Криволинейные интегралы первого и второго рода, его приложения(длина дуги, масса кривой, моменты инерции кривой, координаты центра масс кривой)

Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δs_i длиной Δs_i и выберем на каждой из частей точку M_i. Составим интегральную сумму 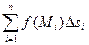. Назовем λ длину наибольшего отрезка кривой.

Определение 10.1. Если существует конечный предел интегральной суммы 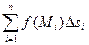, не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек M_i, то он называется криволинейным интегралом первого родаот функции f по кривой L и обозначается

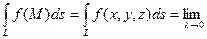
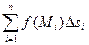. (10.1)