Определение числовых характеристик распределения показателя надежности и графическое построение гистограммы и полигоны
Цель работы: Освоить методику оценки числовых характеристик распределения показателя надёжности
1 Содержание работы: По статистическому ряду распределения показателя надежности (табл.3) определить числовые характеристики показателя надежности и построить гистограмму.
2 Методические указания
2.1 Описать графические методы обработки информации по показателям надежности. Использование ПЭВМ при обработке статистической информации
2.2 Перечислить основные показатели надёжности. Функциональные и вероятностно-статистические подходы к оценке надёжности.
2.3 Определение числовых характеристик распределения показателя надежности.
3.Определение числовых характеристик распределения показателя надежности
Основными числовыми характеристиками распределения показателя надежности являются: среднее значение, среднее квадратическое отклонение и коэффициент вариации [2]:
Среднее значение показателя надежности:
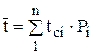 , (1)
, (1)
где 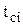 – середина i-го интервала;
– середина i-го интервала;
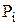 - опытная вероятность в i-ом интервале.
- опытная вероятность в i-ом интервале.
Подставляя значение из статистического ряда из таблицы 3, получаем среднее значение полного ресурса:
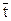 =1,65·0,125+3,15·0,406+4,65·0,188+6,15·0,156+7,65·0,031+
=1,65·0,125+3,15·0,406+4,65·0,188+6,15·0,156+7,65·0,031+
+9,15·0,094=4,42 (тыс. мото-ч).
Среднее квадратическое отклонение:
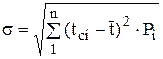 . (2)
. (2)
Подставляя значение статистического ряда из таблицы 3, получим
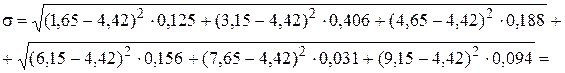
=2,13 (тыс. мото-ч).
Коэффициент вариации определяют по формуле:
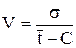 , (3)
, (3)
где 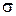 - среднее квадратическое отклонение;
- среднее квадратическое отклонение;
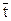 - среднее значение показателя надежности;
- среднее значение показателя надежности;
С - начало первого интервала или начало поля рассеивания.
С определяется по формуле:
С = 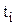 — 0,5А, (4)
— 0,5А, (4)
где 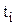 - наименьшее значение показателя надежности.
- наименьшее значение показателя надежности.
Для нашего примера 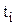 =900 мото-ч (таблица 2).
=900 мото-ч (таблица 2).
А - величина интервала.
Для нашего примера А =1500 мото-ч.
Тогда, по формуле (8):
С= 900 - 0,5·1500= 150 мото-ч.
Ввиду незначительной величины смещения поля рассеивания для нашего примера при дальнейших расчетах принимают С=0. Тогда коэффициент вариации по формуле (3), составит:
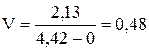 .
.
4 Проверка исходной информации на наличие выпадающих точек
Проверку информации на наличие выпадающих точек осуществляем по формуле [1]:
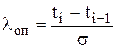 , (5)
, (5)
где 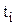 , и
, и 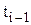 - смежные точки в вариационном ряду информации (таблица 2). Для наименьшего значения ресурса
- смежные точки в вариационном ряду информации (таблица 2). Для наименьшего значения ресурса 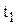 = 0,90;
= 0,90; 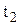 = l,94.
= l,94.
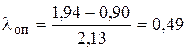 .
.
Для наибольшего значения ресурса 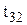 =9.70;
=9.70; 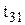 =8.61,
=8.61,
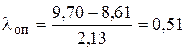 .
.
Полученное значение 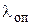 сравнивают с табличными критериями Ирвина
сравнивают с табличными критериями Ирвина 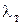 (приложение Г).
(приложение Г).
В нашем случае при N= 32 и доверительной вероятности α = 0,95 табличное значение критерия Ирвина 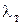 = l,2, то есть больше
= l,2, то есть больше 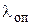 . Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.
. Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.
5 Графическое построение гистограммы и полигоны распределения показателя надежности
Данные статистического ряда (таблица 3) используют для построения графика, наглядно характеризующего опытное распределение показателя надежности (в нашем случае полного ресурса двигателя Д-240): гистограммы (1) и полигона (2) – в соответствии с рисунком 1 и кривой накопленных опытных вероятностей (1) – в соответствии с рисунком 2.
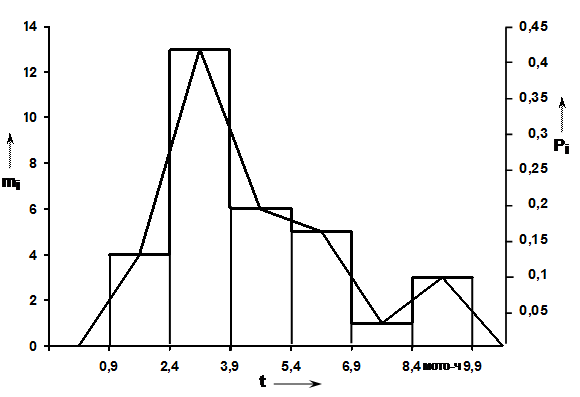 |
Рисунок 1 - Гистограмма (1) и полигон (2) распределения полного ресурса двигателя Д - 240.
6. Контрольные вопросы
6.1 Показатели надёжности. Функциональные и вероятностно-статистические подходы оценки надёжности.
6.2. Показатели надежности как случайные величины. Дискретные и непрерывные случайные величины.
 6.3. Статистические параметры распределения. Среднее арифметическое, мода, медиана, математическое ожидание.
6.3. Статистические параметры распределения. Среднее арифметическое, мода, медиана, математическое ожидание. 

 Меры рассеивания
Меры рассеивания
6.4 Классификация отказов. Физическая и вероятностная модели отказов Основные показатели надежности. Показатели надежности для восстанавливаемых и невосстанавливаемых изделий.
6.5 Функциональные и вероятностно-статистические подходы оценки надёжности.
Практическое занятие № 4
Определение значений интегральной функции теоретического закона распределения f( 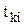 )
)
Цель работы: Освоить методику расчета интегральной функции распределения
1 Содержание работы: Применительно к условиям задания вычислить значения интегральных функций и построить их графики.
2 Методические указания
В теории надежности для выравнивания опытной информации используют большое количество различных законов распределения. К таким законам, например, относятся: нормальный (Гаусса), экспоненциальный, гамма-распределения, Вейбулла, Пуассона, Релля и др.
У каждого закона своя область применения, свои параметры и расчетные уравнения, свои заранее приготовленные таблицы, упрощения проведение расчетов. Применительно к показателям надёжности машин, эксплуатируемых в автомобильном транспорте, в подавляющем большинстве случаев используют закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ).
Каждый закон распределения показателей надёжности характеризуется двумя функциями:
1) дифференциальной функцией или функцией плотности вероятностей;
2) интегральной функцией распределения.
2.1 Перечислить основные показатели надёжности. Показатели безотказности для не восстанавливаемых объектов.
2.2 Интегральные и дифференциальные формы закона распределения времени работы изделия до отказа.
2.3 Определить значения интегральной функции
3. Определение значений интегральной функции ЗНР .
Для ЗНР значения интегральной функции F(tki) в конце i-го интервала определяются по формуле:
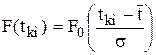 , (1)
, (1)
где F0- так называемая центрированная интегральная функции. Она табулирована и ее значение определяют по приложению 4;
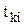 - значение показателя надежности в конце i-го интервала статистического ряда (таблица 3);
- значение показателя надежности в конце i-го интервала статистического ряда (таблица 3);
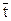 - среднее значение показателя надежности;
- среднее значение показателя надежности;
σ - среднее квадратическое отклонение.
Необходимо помнить, что
F0(-t)=I-F(+t). (2)
4. Определение значений интегральной функции ЗРВ
Для ЗРВ значение интегральной функции F ( 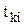 ) в конце i-го интервала определяется по формуле:
) в конце i-го интервала определяется по формуле:
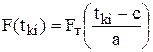 , (3)
, (3)
где 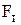 - табулированное значение интегральной функции. Принимается по приложению Ж в зависимости от
- табулированное значение интегральной функции. Принимается по приложению Ж в зависимости от 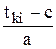 и параметра b;
и параметра b;
с - сдвиг начала рассеивания. Для нашего примера С = 0;
а - параметр ЗРВ определяется по формуле:
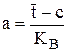 , (4)
, (4)
где 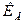 - коэффициент 3PB.
- коэффициент 3PB.
Параметр b и коэффициент 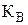 определяется по приложению Е в зависимости от коэффициента вариации.
определяется по приложению Е в зависимости от коэффициента вариации.
Полученные расчетом значения интегральных функций для 3HP и 3PB записывают в таблицу 4.
Таблица 4. – Численные значения интегральных функций теоретических законов распределения
| Интервал, тыс. мото-ч | 0,9- 2,4 | 2,4- 3,9 | 3,9- 5,4 | 5,4- 6,9 | 6,9- 8,4 | 8,4- 9,9 | |
Конец интервала, 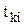 | 2,4 | 3,9 | 5,4 | 6,9 | 8,4 | 9,9 | |
Накопленная вероят-ность (опытная) 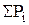 | 0,125 | 0,531 | 0,719 | 0,875 | 0,906 | 1,0 | |
( 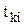 – – 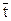 )/σ )/σ | -0,95 | -0,24 | 0,46 | 1,16 | 1,87 | 2,57 | |
F( 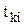 ) ) | 0,17 | 0,40 | 0,68 | 0,88 | 0,97 | 1,0 | |
│ 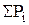 -F( -F( 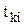 )│ )│ | 0,045 | 0,131 | 0,039 | 0,005 | 0,064 | ||
( 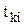 –с)/а –с)/а | 0,48 | 0,78 | 1,09 | 1,39 | 1,69 | 1,99 | |
F( 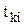 ) ) | 0,18 | 0,43 | 0,70 | 0,87 | 0,96 | 0,99 | |
│ 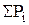 -F( -F( 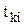 )│ )│ | 0,055 | 0,101 | 0,019 | 0,005 | 0,054 | 0,01 |
5.Построение графика интегральной функции выбранного теоретического закона распределения
По выбранному теоретическому закону распределения (например, ЗРВ) З, наносим на график интервалы и соединяем полученные точки плавной 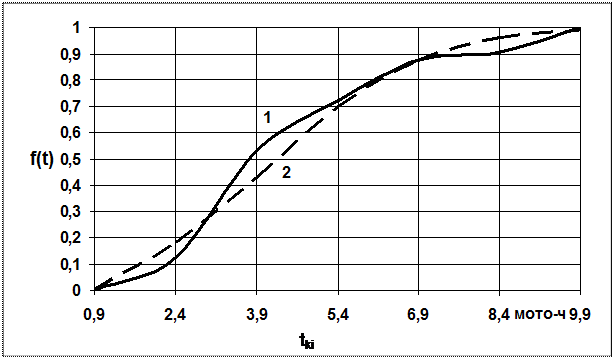 кривой, которая будет теоретической интегральной функцией распределения полного ресурса двигателя в соответствии с рисунком 2.
кривой, которая будет теоретической интегральной функцией распределения полного ресурса двигателя в соответствии с рисунком 2.
Рисунок 2 - Кривая накопленных опытных вероятностей (1) и интегральная функция (2) ЗРВ полного ресурса двигателя
6. Контрольные вопросы
6.1 Функции законов распределения. Нормальный закон распределения Гаусса (ЗНР), экспоненциальный закон распределения (ЭЗР), закон распределения Вейбулла (ЗРВ).
6.2 Использование основных законов распределения для оценки надежности невосстанавливаемых и восстанавливаемых объектов.
6.3 Интегральные и дифференциальные формы закона распределения времени работы изделия до отказа.
6.4 Определение долговечности ремонтопригодности и сохраняемости и их основные показатели. Комплексные показатели готовности.
Практическое занятие № 5
