Полигоны частот. Выборочная функция распределения и гистограммы.

Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x₁, n₁), (x₂, n₂),…, (x_k, n_k), где x_i откладываются на оси абсцисс, а n_i – на оси ординат. Если на оси ординат откладывать не абсолютные (n_i), а относительные (w_i) частоты, то получим полигон относительных частот (рис.1). 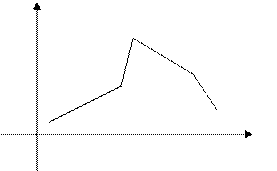Рис. 1.

По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x.

Определение 8.1. Выборочной (эмпирической) функцией распределения называют функцию F*(x), определяющую для каждого значения х относительную частоту события X < x. Таким образом,

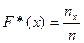, (8.1)

где п_х – число вариант, меньших х, п – объем выборки.

Замечание. В отличие от эмпирической функции распределения, найденной опытным путем, функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. F(x) определяет вероятность события X < x, а F*(x) – его относительную частоту. При достаточно больших п, как следует из теоремы Бернулли, F*(x) стремится по вероятности к F(x).

Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F(x), а именно:

1) 0 ≤ F*(x) ≤ 1.

2) F*(x) – неубывающая функция.

3) Если х₁ – наименьшая варианта, то F*(x) = 0 при х≤ х₁; если х_к – наибольшая варианта, то F*(x) = 1 при х > х_к .

Для непрерывного признака графической иллюстрацией служат гистограммы, то есть ступенчатые фигуры, состоящие из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной n_i /h (гистограмма частот) или w_i /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице (рис.2).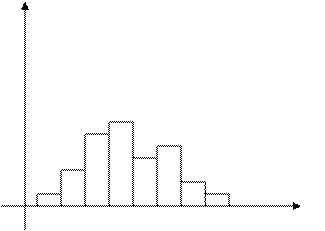

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины или признака.

Определение 8.2. Выборочным среднимназывается среднее арифметическое значений случайной величины, принимаемых в выборке:

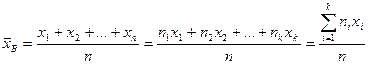, (8.2.)

где x_i – варианты, n_i - частоты.

Замечание. Выборочное среднее служит для оценки математического ожидания исследуемой случайной величины. В дальнейшем будет рассмотрен вопрос, насколько точной является такая оценка.

Определение 8.3. Выборочной дисперсией называется

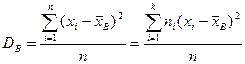
а выборочным средним квадратическим отклонением–

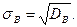(8.3.)

Так же, как в теории случайных величин, можно доказать, что справедлива следующая формула для вычисления выборочной дисперсии:

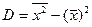. (8.4.)

Пример 1. Найдем числовые характеристики выборки, заданной статистическим рядом

xi
ni

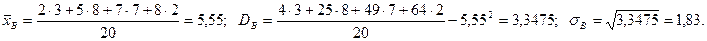Другими характеристиками вариационного ряда являются:

- мода М₀ – варианта, имеющая наибольшую частоту (в предыдущем примере М₀ = 5 ).

- медиана т_е - варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно ( n = 2k + 1 ), то m_e = x_k+1, а при четном n =2k 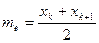. В частности, в примере 1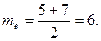

Лекция 9.

Точечные статистические оценки и их виды. Оценки основных параметров генеральной совокупности с помощью выборочных характеристик. Интервальное оценивание неизвестных параметров. Точность оценки, доверительная вероятность (надежность), доверительный интервал. Построение доверительных интервалов для оценки математического ожидания нормального распределения при известной и при неизвестной дисперсии. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения.

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины или признака.

Получив статистические оценки параметров распределения (выборочное среднее, выбороч-ную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближе-нием соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться.

Пусть Θ* - статистическая оценка неизвестного параметра Θ теоретического распределения. Извлечем из генеральной совокупности несколько выборок одного и того же объема п и вычислим для каждой из них оценку параметра Θ: 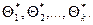Тогда оценку Θ* можно рассматривать как случайную величину, принимающую возможные значения 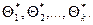Если математическое ожидание Θ* не равно оцениваемому параметру, мы будем получать при вычислении оценок систематические ошибки одного знака (с избытком, если М( Θ*) >Θ, и с недостатком, если М(Θ*) < Θ). Следовательно, необходимым условием отсутствия систе-матических ошибок является требование М(Θ*) = Θ.

Определение 9.1. Статистическая оценка Θ* называется несмещенной, если ее математичес-кое ожидание равно оцениваемому параметруΘ при любом объеме выборки:

М(Θ*) = Θ. (9.1.)

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Однако несмещенность не является достаточным условием хорошего приближения к истин-ному значению оцениваемого параметра. Если при этом возможные значения Θ* могут значительно отклоняться от среднего значения, то есть дисперсия Θ* велика, то значение, найденное по данным одной выборки, может значительно отличаться от оцениваемого параметра. Следовательно, требуется наложить ограничения на дисперсию.

Определение 9.2. Статистическая оценка называется эффективной, если она при заданном объеме выборки п имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется еще и требование состоятельности.

Определение 9.3. Состоятельной называется статистическая оценка, которая при п→∞ стре-мится по вероятности к оцениваемому параметру (если эта оценка несмещенная, то она будет состоятельной, если при п→∞ ее дисперсия стремится к 0).

Убедимся, что 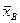представляет собой несмещенную оценку математического ожидания М(Х).

Будем рассматривать 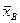как случайную величину, а х₁, х₂,…, х_п, то есть значения исследуемой случайной величины, составляющие выборку,– как независимые, одинаково распределенные случайные величины Х₁, Х₂,…, Х_п, имеющие математическое ожидание а. Из свойств математического ожидания следует, что

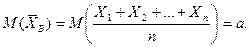
Но, поскольку каждая из величин Х₁, Х₂,…, Х_п имеет такое же распределение, что и генеральная совокупность, а = М(Х), то есть М( 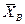) = М(Х), что и требовалось доказать. Выборочное среднее является не только несмещенной, но и состоятельной оценкой математического ожидания. Если предположить, что Х₁, Х₂,…, Х_п имеют ограниченные дисперсии, то из теоремы Чебышева следует, что их среднее арифметическое, то есть 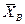, при увеличении п стремится по вероятности к математическому ожиданию а каждой их величин, то есть к М(Х). Следовательно, выборочное среднее есть состоятельная оценка математического ожидания.

В отличие от выборочного среднего, выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Можно доказать, что

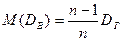, (9.2.)

где D_Г – истинное значение дисперсии генеральной совокупности. Можно предложить другую оценку дисперсии – исправленную дисперсию s², вычисляемую по формуле

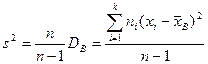. (9.3)

Такая оценка будет являться несмещенной. Ей соответствует исправленное среднее квадратическое отклонение

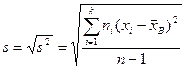. (9.4)

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Поэтому в таком случае лучше пользоваться интервальными оценками, то есть указывать интервал, в который с заданной вероятностью попадает истинное значение оцениваемого параметра. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки Θ* некоторого параметра Θ справедливо неравенство | Θ* - Θ | < δ, число δ > 0 характеризует точность оценки( чем меньше δ, тем точнее оценка). Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью.

Определение 9. 4. Надежностью (доверительной вероятностью)оценки Θ* параметра Θ называется вероятность γ того, что выполняется неравенство | Θ* - Θ | < δ. Если заменить это неравенство двойным неравенством – δ < Θ* - Θ < δ, то получим:

p ( Θ* - δ < Θ < Θ* + δ ) = γ.

Таким образом, γ есть вероятность того, что Θ попадает в интервал ( Θ* - δ, Θ* + δ).

Определение 9.5. Доверительнымназывается интервал, в который попадает неизвестный параметр с заданной надежностью γ.

1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии.

Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего 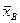оценить ее математическое ожидание а. Будем рассматривать выборочное среднее 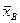как случайную величину 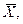а значения вариант выборки х₁, х₂,…, х_п как одинаково распределенные независимые случайные величины Х₁, Х₂,…, Х_п, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М( 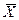) = а, 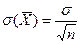(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства 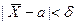. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:

р ( 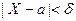) = 2Ф 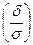. Тогда , с учетом того, что 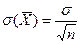, р ( 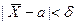) = 2Ф =

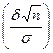=2Ф( t ), где 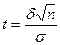. Отсюда 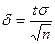, и предыдущее равенство можно переписать так:

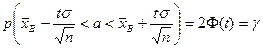. (9.5)

Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал 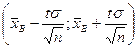, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.

Пример. Найдем доверительный интервал для математического ожидания нормально распреде-ленной случайной величины, если объем выборки п = 49, 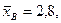σ = 1,4, а доверительная вероятность γ = 0,9.

Определим t, при котором Ф(t) = 0,9:2 = 0,45: t = 1,645. Тогда

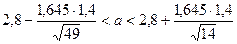, или 2,471 < a < 3,129. Найден доверительный интервал, в который попадает а с надежностью 0,9.

2. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии.

Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то доверительный интервал для ее математического ожидания имеет вид .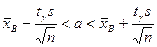

где 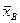- выборочное среднее, s – исправленная дисперсия, п – объем выборки.

Таким образом, получен доверительный интервал для а, где t_γ можно найти по соответствующей таблице при заданных п и γ.

Пример. Пусть объем выборки п = 25, 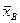= 3, s = 1,5. Найдем доверительный интервал для а при γ = 0,99. Из таблицы находим, что t_γ (п = 25, γ = 0,99) = 2,797. Тогда 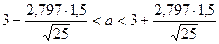, или 2,161< a < 3,839 – доверительный интервал, в который попадает а с вероятностью 0,99.

3. Доверительный интервал для оценки среднего квадратического отклонения нормального распределения имеет вид

.

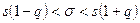Замечание. Если q > 1, то с учетом условия σ > 0 доверительный интервал для σ будет иметь границы

.

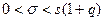Пример.

Пусть п = 20, s = 1,3. Найдем доверительный интервал для σ при заданной надежности γ = 0,95. Из соответствующей таблицы находим q (n = 20, γ = 0,95 ) = 0,37. Следовательно, границы доверительного интервала: 1,3(1-0,37) = 0,819 и 1,3(1+0,37) = 1,781. Итак, 0,819 < σ < 1,781 с вероятностью 0,95.

Лекция 10. Элементы теории корреляции. Нахождение выборочных уравнений прямых линий регрессии по несгруппированным данным и по корреляционной таблице.

Рассмотрим выборку двумерной случайной величины (Х, Y) . Примем в качестве оценок условных математических ожиданий компонент их условные средние значения, а именно: условным средним 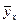назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее 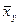-среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. Уравнения регрессии Y на Х и Х на Y

имеют вид :

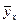=f*(x) -

- выборочное уравнение регрессии Y на Х,

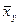= φ*(у) -

- выборочное уравнение регрессии Х на Y.

Соответственно функции f*(x) и φ*(у) называются выборочной регрессией Y на Х и Х на Y, а их графики – выборочными линиями регрессии. Выясним, как определять параметры выборочных уравнений регрессии, если сам вид этих уравнений известен.

Пусть изучается двумерная случайная величина (Х, Y), и получена выборка из п пар чисел (х₁, у₁), (х₂, у₂),…, (х_п, у_п). Будем искать параметры прямой линии регрессии Y на Х вида

Y = ρ_yxx + b , (10.1)

подбирая параметры ρ_ух и b так, чтобы точки на плоскости с координатами (х₁, у₁), (х₂, у₂), …, (х_п, у_п) лежали как можно ближе к прямой (10.1). Используем для этого метод наименьших квадратов и найдем минимум функции

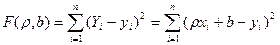. (10.2)

Приравняем нулю соответствующие частные производные:

.

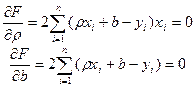В результате получим систему двух линейных уравнений относительно ρ и b:

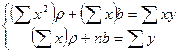. (10.3)

Ее решение позволяет найти искомые параметры в виде:

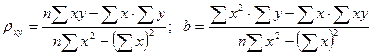. (10.4)

При этом предполагалось, что все значения Х и Y наблюдались по одному разу.

Теперь рассмотрим случай, когда имеется достаточно большая выборка (не менее 50 значений), и данные сгруппированы в виде корреляционной таблицы:

Y	X
x1	x2	…	xk	ny
y1 y2 … ym	n11 n12 … n1m	n21 n22 … n2m	… … … …	nk1 nk2 … nkm	n11+n21+…+nk1 n12+n22+…+nk2 …………….. n1m+n2m+…+nkm
nx	n11+n12+…+n1m	n21+n22+…+n2m	…	nk1+nk2+…+nkm	n=∑nx = ∑ny

Здесь n_ij – число появлений в выборке пары чисел (x_i, y_j).

Поскольку 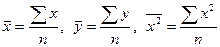, заменим в системе (10.3)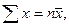

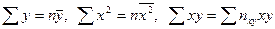, где п_ху – число появлений пары чисел (х, у). Тогда система (10.3) примет вид:

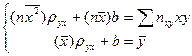. (10.5)

Можно решить эту систему и найти параметры ρ_ух и b, определяющие выборочное уравнение прямой линии регрессии:

.

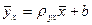Но чаще уравнение регрессии записывают в ином виде, вводя выборочный коэффициент корреляции. Выразим b из второго уравнения системы (10.5):

.

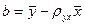Подставим это выражение в уравнение регрессии: 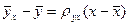. Из (10.4)

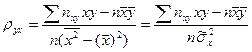, (10.6)

где 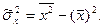Введем понятие выборочного коэффициента корреляции

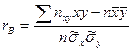
и умножим равенство (4.12) на 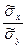: 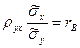, откуда 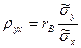. Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида

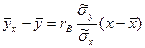. (10.7)

Лекция 11.

Статистическая проверка статистических гипотез. Общие принципы проверки гипотез. Понятия статистической гипотезы (простой и сложной), нулевой и конкурирующей гипотезы, ошибок первого и второго рода, уровня значимости, статистического критерия, критической области, области принятия гипотезы. Наблюдаемое значение критерия. Критические точки. Мощность критерия. Критерии для проверки гипотезы о вероятности события.

Определение 11.1. Статистической гипотезой называют гипотезу о виде неизвестного распределения генеральной совокупности или о параметрах известных распределений.

Определение 11.2. Нулевой (основной) называют выдвинутую гипотезу Н₀. Конкурирую-щей (альтернативной)называют гипотезу Н₁, которая противоречит нулевой.

Пример. Пусть Н₀ заключается в том, что математическое ожидание генеральной совокупности а = 3. Тогда возможные варианты Н₁: а) а ≠ 3; б) а > 3; в) а < 3.

Определение 11.3. Простой называют гипотезу, содержащую только одно предположение, сложной – гипотезу, состоящую из конечного или бесконечного числа простых гипотез.

Пример. Для показательного распределения гипотеза Н₀: λ = 2 – простая, Н₀: λ > 2 – сложная, состоящая из бесконечного числа простых ( вида λ = с, где с – любое число, большее 2).

В результате проверки правильности выдвинутой нулевой гипотезы ( такая проверка называется статистической, так как производится с применением методов математичес-кой статистики) возможны ошибки двух видов: ошибка первого рода, состоящая в том, что будет отвергнута правильная нулевая гипотеза, и ошибка второго рода, заключаю-щаяся в том, что будет принята неверная гипотеза.

Замечание. Какая из ошибок является на практике более опасной, зависит от конкретной задачи. Например, если проверяется правильность выбора метода лечения больного, то ошибка первого рода означает отказ от правильной методики, что может замедлить лече-ние, а ошибка второго рода (применение неправильной методики) чревата ухудшением состояния больного и является более опасной.

Определение 11.4. Вероятность ошибки первого рода называется уровнем значимости α.

Основной прием проверки статистических гипотез заключается в том, что по имеющейся выборке вычисляется значение некоторой случайной величины, имеющей известный закон распределения.

Определение 11.5.Статистическим критерием называется случайная величина К с известным законом распределения, служащая для проверки нулевой гипотезы.

Определение 11.6. Критической областью называют область значений критерия, при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают.

Итак, процесс проверки гипотезы состоит из следующих этапов:

1) выбирается статистический критерий К;

2) вычисляется его наблюдаемое значение К_набл по имеющейся выборке;

3) поскольку закон распределения К известен, определяется (по известному уровню значимости α) критическое значениеk_кр, разделяющее критическую область и область принятия гипотезы (например, если р(К > k_кр) = α, то справа от k_кр распо-лагается критическая область, а слева – область принятия гипотезы);

4) если вычисленное значение К_набл попадает в область принятия гипотезы, то нулевая гипотеза принимается, если в критическую область – нулевая гипотеза отвергается.

Различают разные виды критических областей:

- правостороннююкритическую область, определяемую неравенством K > k_кр ( k_кр > 0);

- левостороннюю критическую область, определяемую неравенством K < k_кр ( k_кр < 0);

- двустороннюю критическую область, определяемую неравенствами K < k₁, K > k₂ (k₂ > k₁).

Определение 11.7. Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что верна конкурирующая гипотеза.

Если обозначить вероятность ошибки второго рода (принятия неправильной нулевой гипотезы) β, то мощность критерия равна 1 – β. Следовательно, чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода. Поэтому после выбора уровня значимости следует строить критическую область так, чтобы мощность критерия была максимальной.

Критерий для проверки гипотезы о вероятности события.

Пусть проведено п независимых испытаний (п – достаточно большое число), в каждом из которых некоторое событие А появляется с одной и той же, но неизвестной вероятностью р, и найдена относительная частота 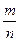появлений А в этой серии испытаний. Проверим при заданном уровне значимости α нулевую гипотезу Н₀, состоящую в том, что вероятность р равна некоторому значению р₀.

Примем в качестве статистического критерия случайную величину

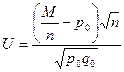, (11.1)

имеющую нормальное распределение с параметрами M(U) = 0, σ(U) = 1 (то есть нормиро-ванную). Здесь q₀ = 1 – p₀. Вывод о нормальном распределении критерия следует из теоремы Лапласа (при достаточно большом п относительную частоту можно приближенно считать нормально распределенной с математическим ожиданием р и средним квадрати-ческим отклонением ).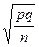

Критическая область строится в зависимости от вида конкурирующей гипотезы.

1) Если Н₀: р = р₀, а Н₁: р ≠ р₀, то критическую область нужно построить так, чтобы вероятность попадания критерия в эту область равнялась заданному уровню значимости α. При этом наибольшая мощность критерия достигается тогда, когда критическая область состоит из двух интервалов, вероятность попадания в каждый из которых равна 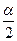. Поскольку U симметрична относительно оси Оу, вероятность ее попадания в интервалы (-∞; 0) и (0; +∞) равна 0,5, следовательно, критическая область тоже должна быть симметрична относительно Оу. Поэтому и_кр определяется по таблице значений функции Лапласа из условия 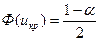, а критическая область имеет вид .

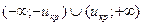Замечание. Предполагается, что используется таблица значений функции Лапласа, заданной в виде 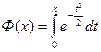, где нижний предел интегрирования равен 0, а не -∞. Функция Лапласа, заданная таким образом, является нечетной, а ее значения на 0,5 меньше, чем значения стандартной функции Ф(х) (см. лекцию 6).

Далее нужно вычислить наблюдаемое значение критерия:

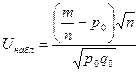. (11.2)

Если |U_набл| < u_кр, то нулевая гипотеза принимается.

Если |U_набл| > u_кр, то нулевая гипотеза отвергается.

2) Если конкурирующая гипотеза Н₁: р > p₀, то критическая область определяется неравенством U > u_кр, то есть является правосторонней, причем р(U > u_кр) = α. Тогда 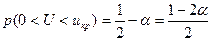. Следовательно, и_кр можно найти по таблице значений функции Лапласа из условия, что 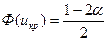. Вычислим наблюдаемое значение критерия по формуле (19.2).

Если U_набл < u_кр, то нулевая гипотеза принимается.

Если U_набл > u_кр, то нулевая гипотеза отвергается.

3) Для конкурирующей гипотезы Н₁: р < p₀ критическая область является левосторонней и задается неравенством U <- u_кр, где и_кр вычисляется так же, как в предыдущем случае.

Если U_набл > - u_кр, то нулевая гипотеза принимается.

Если U_набл < - u_кр, то нулевая гипотеза отвергается.

Пример. Пусть проведено 50 независимых испытаний, и относительная частота появления события А оказалась равной 0,12. Проверим при уровне значимости α = 0,01 нулевую гипотезу Н₀: р = 0,1 при конкурирующей гипотезе Н₁: р > 0,1. Найдем 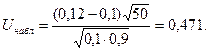Критическая область является правосторонней, а и_кр нахо-дим из равенства Ф(и_кр) = 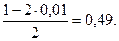Из таблицы значений функции Лапласа определяем и_кр = 2,33. Итак, U_набл < u_кр, и гипотеза о том, что р = 0,1, принимается.

Лекция 12.