Решение показательных, логарифмических уравнений и неравенств
Цель: Знать методы решения показательных и логарифмических уравнений и неравенств, уметь применять их при решении соответствующих заданий.
Методические рекомендации
Степени чисел от 0 до 10
| n | ||||||||||||
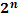 | ||||||||||||
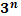 | ||||||||||||
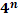 | ||||||||||||
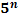 | ||||||||||||
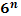 | ||||||||||||
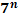 | ||||||||||||
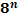 | ||||||||||||
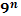 | ||||||||||||
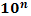 | ||||||||||||
Решение квадратных уравнений: 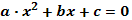 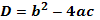 , Если , Если 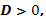 то то 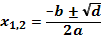 Если Если 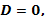 то то 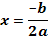 Если Если 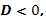 то корней нет то корней нет | Формулы сокращенного умножения: 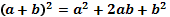 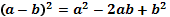 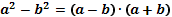 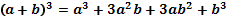 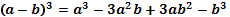 | |||||||||||
| Свойства степеней | Свойства корней n-ой степени | |||||||||||
1. 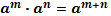 2. 2. 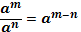 3. 3. 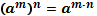 4. 4. 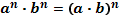 5. 5. 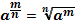 6. 6. 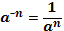 7. 7. 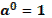 8. 8. 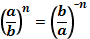 9. 9. 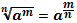 | 1. 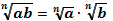 2. 2. 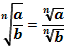 3. 3. 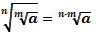 4. 4. 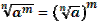 5. 5. 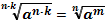 6. 6. 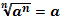 7. 7. 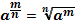 | |||||||||||
Используя предложенные методические рекомендации и методические рекомендации к самостоятельной работе №9, выполните задания:
| 1 вариант | 2 вариант |
1. Решить уравнения: а)  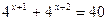 ; б) ; б) 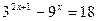 ; в) ; в) 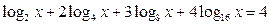 ; г) ; г) 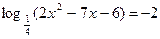 ; д) ; д) 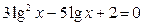 . . | 1. Решить уравнения: а) 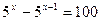 ; б) ; б) 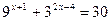 ; в) ; в) 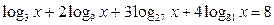 ; г) ; г) 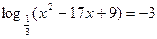 ; д) ; д) 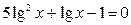 . . |
2. Решить неравенства: а) 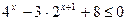 ; б) ; б) 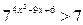 ; в) ; в) 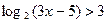 ; г) ; г) 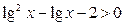 . . | 2. Решить неравенства: а) 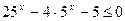 ; б) ; б) 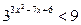 ; в) ; в) 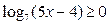 ; г) ; г) 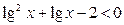 . . |
Самостоятельная работа № 9.
Решение тригонометрических уравнений повышенной сложности
Цель: Знать методы решения тригонометрических уравнений, формулы для нахождения корней, уметь использовать полученные знания при решении уравнений повышенной сложности.
Методические рекомендации
I. Решение простейших тригонометрических уравнений.
| Уравнение | Формулы решения | Частные случаи |
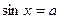 | при 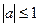 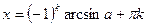 , , 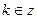 при при 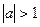 - решений нет - решений нет | 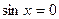 ; ; 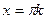 , , 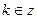 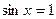 ; ; 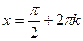 , , 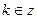 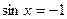 , , 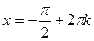 , , 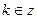 |
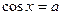 | при 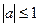 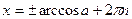 , , 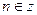 при при 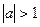 - решений нет - решений нет | 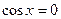 ; ; 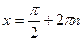 , , 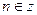 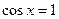 ; ; 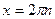 , , 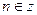 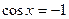 ; ; 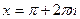 , , 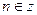 |
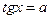 | 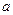 - любое число - любое число 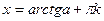 , , 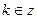 | - |
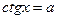 | 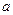 - любое число - любое число 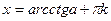 , , 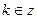 | - |
II. Тригонометрические уравнения.
| Уравнение | Способ решения | Формулы |
1. Уравнение содержит только синусы или косинусы (синусы и косинусы) вида 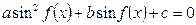 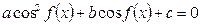 и т.д. и т.д. | Уравнение сводится к квадратному (биквадратному) относительно синуса (косинуса) | 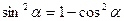 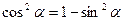 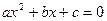 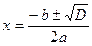 |
2. Однородное уравнение I степени вида 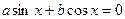 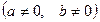 | Деление обеих частей на 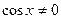 . Получаем: . Получаем: 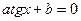 | 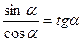 |
3. Однородное уравнение II степени вида 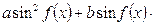 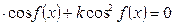 | Деление обеих частей на 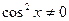 . Получаем: . Получаем: 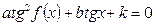 | 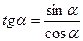 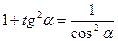 |
4. Уравнение вида 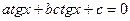 | Уравнение сводится к квадратному относительно тангенса заменой 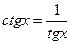 | 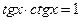 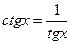 |
III. Основные тригонометрические тождества.
1. 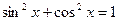 ;
; 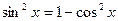 ;
; 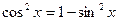
2. 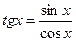
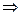
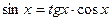
3. 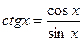
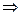
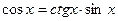
4. 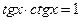
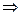
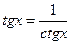 и
и 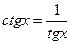
5. 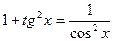
6. 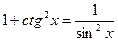
IV. Формулы сложения.
1. 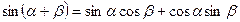
2. 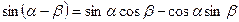
3. 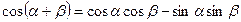
4. 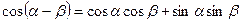
5. 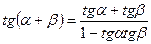
6. 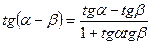
V. Формулы двойного и половинного аргументов.
1. 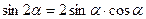
2. 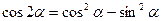 ;
; 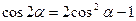 ;
; 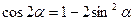
3. 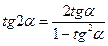
4. 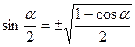
5. 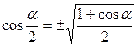
6. 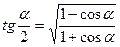
VI. Формулы суммы и разности одноименных тригонометрических функций.
1. 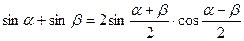
2. 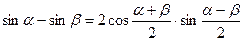
3. 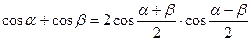
4. 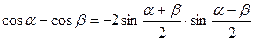
5. 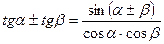
Значения тригонометрических функций
| град | 00 | 300 | 450 | 600 | 900 |
| радиан | 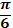 | 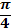 | 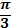 | 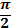 | |
sin 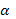 |  | 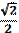 | 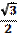 | ||
cos 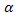 | 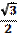 | 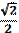 |  | ||
tg 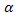 | 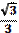 | 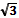 | не существ | ||
ctg 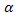 | Не существ | 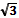 | 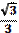 |
Используя методические рекомендации, решите уравнения:
1. 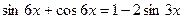 ;
;
2. 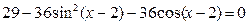 ;
;
3. 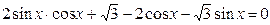 ;
;
4. 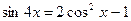 ;
;
5. 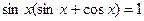 ;
;
6. 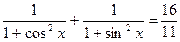 .
.
Подсказки.
1. Воспользуйтесь формулой двойного угла для 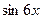 и
и 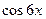 .
.
2. Обозначьте 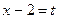 , решите уравнение, сведя его к квадратному с помощью формулы
, решите уравнение, сведя его к квадратному с помощью формулы 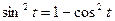 .
.
3. Сгруппируйте 1-ое и 3-е слагаемые, примените разложение на множители.
4. Воспользуйтесь формулой двойного угла для 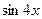 и
и 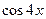 , формулой понижения степени
, формулой понижения степени 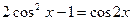 .
.
5. Раскройте скобки, примените основное тригонометрическое тождество.
6. Приведите дроби к общему знаменателю, а затем используйте основное тригонометрическое тождество 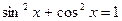 , сведите уравнение к квадратному
, сведите уравнение к квадратному
Самостоятельная работа № 10.
Решение прикладных задач
Цель: Уметь применять определение производной и ее механический смысл к решению прикладных задач.
Методические рекомендации
Физический смысл первой производной.
Физический смысл производной заключается в том, что мгновенная скорость движения 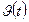 в момент времени t есть производная пути по времени, т.е.
в момент времени t есть производная пути по времени, т.е.
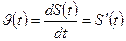
Физический смысл второй производной.
Ускорение прямолинейного движения в данный момент времени есть первая производная скорости по времени или вторая производная пути по времени.
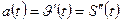
Пример.
1. Зависимость пути от времени при прямолинейном движении точки задана уравнением
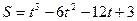 .
.
В какой момент времени ускорение движения точки будет равно 24 м/с2?
Решение.
а) Найдем скорость движения точки по формуле: 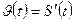
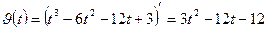
б) Найти ускорение движения точки по формуле: 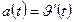
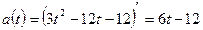
в) Из условия 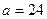 м/с2, найти момент времени:
м/с2, найти момент времени:
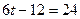
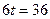
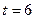 c
c
Ответ: 6 с.
v Правила дифференцирования и таблица производных основных функций.
Правила.
1. 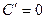 | 4. 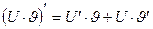 |
2. 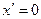 | 5. 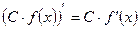 |
3. 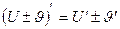 | 6. 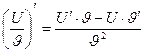 |
Производные основных элементарных функций.
1. 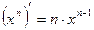 , , 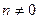 | 8. 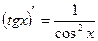 |
2. 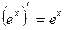 | 9. 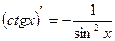 |
3. 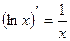 | 10. 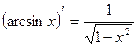 |
4. 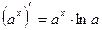 | 11. 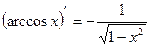 |
5. 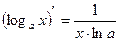 | 12. 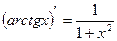 |
6. 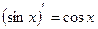 | 13. 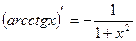 |
7. 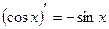 |
Используя методические рекомендации, выполните задания:
| 1 вариант | 2 вариант |
1. Тело движется вверх по закону 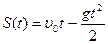 с начальной скоростью с начальной скоростью 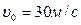 , , 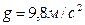 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 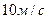 ? ? | 1. Тело движется вверх по закону 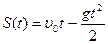 с начальной скоростью с начальной скоростью 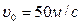 , , 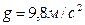 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 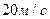 . . |
2. Найдите силу, действующую на тело массой 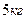 , движущееся по закону , движущееся по закону 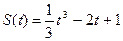 в момент времени в момент времени 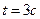 . . | 2. Тело массой 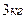 движется по прямой согласно уравнению движется по прямой согласно уравнению 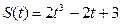 . Найдите действующую на него силу в момент времени . Найдите действующую на него силу в момент времени 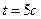 . . |
3. Определить кинетическую энергию точки, массой 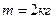 , движущейся по закону , движущейся по закону 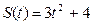 в момент времени в момент времени 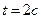 . . | 3. Определить кинетическую энергию точки, массой 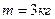 , движущейся по закону , движущейся по закону 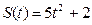 в момент времени в момент времени 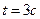 . . |
4.Точка движется по прямой по закону 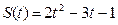 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 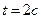 . . | 4. Точка движется по прямой по закону 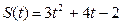 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 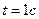 . . |
.
Самостоятельная работа № 11.
