Оренбургского района Оренбургской области
Оренбургского района Оренбургской области


ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
«Загадка чисел
Фибоначчи»


Выполнила:Каналиева Дана
ученица 6 класса
Научный руководитель:
Газизова Валерия Валерьевна
учитель математики высшей категории
п. Экспериментальный
2012г
Оглавление
Пояснительная записка……………………………………………………………………........ 3.
Введение. История чисел Фибоначчи.……………………………………………………...... 4.
Глава 1. Числа Фибоначчи в живой природе.......……. …………………………………... 5.
Глава 2. Спираль Фибоначчи .......................................................……………..... 9.
Глава 3. Числа Фибоначчи в изобретениях человека .........…………………………….. 13
Глава 4. Наши исследования……………………………………………………………….... 16.
Глава 5. Заключение, выводы……………………………………………………………...... 19.
Список используемой литературы и сайтов Интернета…………………………………........21.
- Объект исследования:
- человек, математические абстракции, созданные человеком, изобретения человека, окружающий растительный и животный мир.
- Предмет исследования:
- форма и строение исследуемых предметов и явлений.
- Цель исследования:
изучить проявление чисел Фибоначчи и связанного с ним закона золотого сечения в строении живых и неживых объектов,
найти примеры использования чисел Фибоначчи.
- Задачи работы:
- Описать способ построения ряда Фибоначчи и спирали Фибоначчи.
- Увидеть математические закономерности, в строении человека, растительного мира и неживой природы с точки зрения феномена Золотого сечения.
- Новизна исследования:
- Открытие чисел Фибоначчи в окружающей нас действительности.
· Практическая значимость:
· Использование приобретенных знаний и навыков исследовательской работы при изучении других школьных предметов.
· Умения и навыки:
· Организация и проведение эксперимента.
· Использование специальной литературы.
· Приобретение умения делать обзор собранного материала (доклад, презентацию)
· Оформление работы рисунками, диаграммами, фотографиями.
· Активное участие в обсуждении своей работы.
· Методы исследования:
· эмпирический (наблюдение, эксперимент, измерение).
· теоретический (логическая ступень познания).
Пояснительная записка.
«Числа управляют миром! Число – это сила, царящая над богами и смертными!» - так говорили ещё древние пифагорейцы. Актуальна ли в наши дни эта основа учения Пифагора? Изучая в школе науку чисел, нам хочется убедиться в том, что действительно, явления всей Вселенной подчинены определенным числовым соотношениям, найти эту невидимую связь между математикой и жизнью!
Неужели в каждом цветочке,
И в молекуле, и в галактике,
Числовые закономерности
Этой строгой «сухой» математики?
Мы обратились к современному источнику информации – к Интернету и прочитали о числах Фибоначчи, о магических числах, которые таят в себе великую загадку. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах...
Почему же эта последовательность чисел столь распространена в нашем мире?
Мы захотели узнать о тайнах чисел Фибоначчи. Результатом нашей деятельности и явилась данная исследовательская работа.
- Гипотеза:
- в окружающей нас действительности всё построено по удивительно гармоничным законам с математической точностью.
- Всё в мире продуманно и просчитано самым главным нашим дизайнером – Природой!
Спираль Фибоначчи.
В математике нет иной формы, которая обладала бы такими же уникальными свойствами, как спираль, потому, что
в основе строения спирали лежит правило Золотого сечения!
Чтобы понять математическое построение спирали, повторим, что такое Золотое сечение.
Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, или, другими словами, меньший отрезок так относится к большему, как больший ко всему.


То есть (a+b) /a = a / b
Прямоугольник с именно таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,168 : 1.
Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника,
мы снова получим золотой прямоугольник меньших размеров.


Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов.
Например, спиралевидную форму можно увидеть и в расположении семян подсолнечника, в ананасах, кактусах, строении лепестков роз и так далее.


Нас удивляет и восхищает спиральное строение ракушек.



У большинства улиток, которые обладают раковинами, раковина растет в форме спирали. Однако нет сомнения, что эти неразумные существа не имеют представления не только о спирали, но не обладают даже простейшими математическими знаниями, чтобы самим создать себе спиралевидную раковину.
Но тогда как же эти неразумные существа смогли определить и избрать для себя идеальную форму роста и существования в виде спиральной раковины? Могли ли эти живые существа, которых ученых мир называет примитивными формами жизни, рассчитать, что идеальной для их существования будет спиральная форма ракушки?
Пытаться объяснить происхождение подобной даже самой примитивной формы жизни случайным стечением неких природных обстоятельств по меньшей мере абсурдно. Совершенно ясно, что этот проект является осознанным творением.
Спирали есть и в человеке. С помощью спиралей мы слышим:

Также, во внутреннем ухе человека имеется орган Cochlea ("Улитка"), который исполняет функцию передачи звуковой вибрации. Эта костевидная структура наполнена жидкостью и сотворена в форме улитки, имеющей в себе золотые пропорции.


Спирали есть на наших ладошках и пальцах:


В животном мире мы также можем найти множество примеров спиралей.
В форме спирали развиваются рога и бивни животных, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.



Интересно, что спиралью закручивается ураган, облака циклона и это хорошо видно из космоса:



В океанских и морских волнах спираль можно математически отразить на графике с точками 1,1,2,3,5,8,13,21,34 и 55.


Такую «бытовую» и «прозаическую» спираль тоже все узнают.
Ведь вода убегает из ванной по спирали:

Да и живём мы с вами в спирали, ведь галактика – это спираль, соответствующая формуле Золотого сечения!

Итак, мы выяснили, что если взять Золотой прямоугольник и разбить его на более мелкие прямоугольники в точной последовательности Фибоначчи, а потом каждый из них разделить в таких пропорциях еще и еще, то получится система, которая называется спираль Фибоначчи.
Эту спираль мы обнаружили в самых неожиданных предметах и явлениях. Теперь понятно, почему спираль называют ещё «кривой жизни».
Спираль стала символом эволюции, ведь и развивается всё именно по спирали.
Шаг 2.
Возьмём тысячелистник:

Внимательно рассмотрим строение стеблей и цветов:

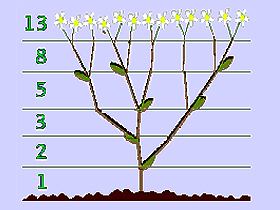
Заметим, что каждая новая ветвь тысячелистника растет из пазухи, и от новой ветви растут новые ветви. Складывая старые и новые ветви, мы нашли число Фибоначчи в каждой горизонтальной плоскости.
Шаг 3.
А проявляются ли числа Фибоначчи в морфологии различных организмов? Рассмотрим всем известного комара:


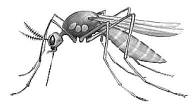
Видим: 3 пары ног, голове 5 усиков – антенн, брюшко делится на 8 сегментов.
Шаг 4.
Найдём пропорции различных частей нашего тела, и убедимся, что они действительно составляют число, очень близкое к золотому сечению.
Занесём данные измерений и вычислений в таблицу.

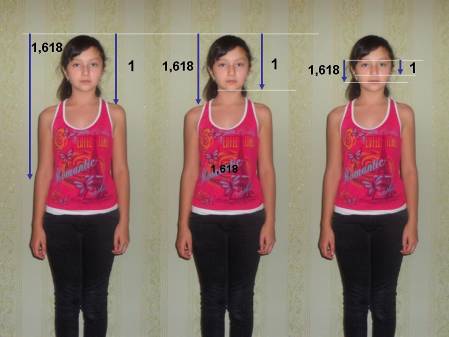
| № | t/s | Наши измерения (в см.) |
| 1. | расстояние от кончиков пальцев до запястья / от запястья до локтя | 37 / 22 ≈ 1,62 ≈ 1,618 |
| 2. | расстояние от уровня плеча до макушки головы /от плеча до бровей | 29 / 18 ≈ 1,61 ≈ 1,618 |
| 3. | длина головы / ширина головы | 24 / 14,8 ≈ 1,62 ≈ 1,618 |
| 4. | От макушки головы до пупка/от макушки головы до плеча | 47 / 29 ≈ 1,63 ≈ 1, 618 |
| 5. | От макушки головы до плеча/ длина головы | 29 / 18 ≈ 1,61 ≈ 1, 618 |
| 6. | От бровей до середины губ/ от бровей до основания носа | 8 / 5 ≈ 1, 6 ≈ 1, 618 |
Видим, что пропорция "фи", которая равна отношению соседних чисел из ряда Фибоначчи , проявляется и в человеческом теле.
Вывод:
В наших исследованиях мы увидели, что в окружающих нас растениях, живых организмах и даже в строении человека проявляют себя числа из последовательности Фибоначчи, что отражает гармоничность их строения.
Сосновая шишка, тысячелистник, комар, человек устроены с математической точностью.
Мы искали ответ на вопрос: как проявляет себя ряд Фибоначчи в окружающей нас действительности? Но, отвечая на него, получали новые и новые вопросы.
Откуда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Спираль скручивается или раскручивается?
Как удивительно человек познаёт этот мир!!!
Найдя ответ на один вопрос, получает следующий. Разгадает его, получает два новых. Разберётся с ними, появятся ещё три. Решив и их, обзаведётся пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55...
Узнаёте?
Заключение.
Самим творцом во все объекты
Заложен уникальный код,
И тот, кто дружен с математикой,
Его познает и поймёт!
Мы изучили и проанализировали проявление чисел последовательности Фибоначчи в окружающей нас действительности. Также мы узнали, что закономерности этого числового ряда, в том числе и закономерности «Золотой» симметрии, проявляются в энергетических переходах элементарных частиц, в планетарных и космических системах, в генных структурах живых организмов.
Мы обнаружили удивительную математическую связь между числом спиралей у растений, числом веток в любой горизонтальной плоскости и числами в последовательности Фибоначчи. Мы увидели, как морфология различных организмов тоже подчиняется этому таинственному закону. Также мы увидели строгую математику в строении человека. Молекула ДНК человека, в которой зашифрована вся программа развития человеческого существа, дыхательная система, строение уха, - всё подчиняется определённым числовым соотношениям.
Мы узнали, что сосновые шишки, раковины улиток, волны океана, рога животных, облака циклона и галактики – все они образуют логарифмические спирали. Даже человеческий палец, который составлен из трех фаланг, находящихся по отношению друг к другу в Золотой пропорции, принимает спиральную форму, когда сжимается.
Вечность времени и световые годы космоса разделяют сосновую шишку и спиральную галактику, но строение остаётся тем же самым: коэффициент 1,618! Возможно, это первостепенный закон, управляющий природными явлениями.
Оренбургского района Оренбургской области


ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
«Загадка чисел
Фибоначчи»


Выполнила:Каналиева Дана
ученица 6 класса
Научный руководитель:
Газизова Валерия Валерьевна
учитель математики высшей категории
п. Экспериментальный
2012г
Оглавление
Пояснительная записка……………………………………………………………………........ 3.
Введение. История чисел Фибоначчи.……………………………………………………...... 4.
Глава 1. Числа Фибоначчи в живой природе.......……. …………………………………... 5.
Глава 2. Спираль Фибоначчи .......................................................……………..... 9.
Глава 3. Числа Фибоначчи в изобретениях человека .........…………………………….. 13
Глава 4. Наши исследования……………………………………………………………….... 16.
Глава 5. Заключение, выводы……………………………………………………………...... 19.
Список используемой литературы и сайтов Интернета…………………………………........21.
- Объект исследования:
- человек, математические абстракции, созданные человеком, изобретения человека, окружающий растительный и животный мир.
- Предмет исследования:
- форма и строение исследуемых предметов и явлений.
- Цель исследования:
изучить проявление чисел Фибоначчи и связанного с ним закона золотого сечения в строении живых и неживых объектов,
найти примеры использования чисел Фибоначчи.
- Задачи работы:
- Описать способ построения ряда Фибоначчи и спирали Фибоначчи.
- Увидеть математические закономерности, в строении человека, растительного мира и неживой природы с точки зрения феномена Золотого сечения.
- Новизна исследования:
- Открытие чисел Фибоначчи в окружающей нас действительности.
· Практическая значимость:
· Использование приобретенных знаний и навыков исследовательской работы при изучении других школьных предметов.
· Умения и навыки:
· Организация и проведение эксперимента.
· Использование специальной литературы.
· Приобретение умения делать обзор собранного материала (доклад, презентацию)
· Оформление работы рисунками, диаграммами, фотографиями.
· Активное участие в обсуждении своей работы.
· Методы исследования:
· эмпирический (наблюдение, эксперимент, измерение).
· теоретический (логическая ступень познания).
Пояснительная записка.
«Числа управляют миром! Число – это сила, царящая над богами и смертными!» - так говорили ещё древние пифагорейцы. Актуальна ли в наши дни эта основа учения Пифагора? Изучая в школе науку чисел, нам хочется убедиться в том, что действительно, явления всей Вселенной подчинены определенным числовым соотношениям, найти эту невидимую связь между математикой и жизнью!
Неужели в каждом цветочке,
И в молекуле, и в галактике,
Числовые закономерности
Этой строгой «сухой» математики?
Мы обратились к современному источнику информации – к Интернету и прочитали о числах Фибоначчи, о магических числах, которые таят в себе великую загадку. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах...
Почему же эта последовательность чисел столь распространена в нашем мире?
Мы захотели узнать о тайнах чисел Фибоначчи. Результатом нашей деятельности и явилась данная исследовательская работа.
- Гипотеза:
- в окружающей нас действительности всё построено по удивительно гармоничным законам с математической точностью.
- Всё в мире продуманно и просчитано самым главным нашим дизайнером – Природой!
