Решение эллиптического разностного уравнения

Примем λ = 1, т. е. h = k (выводы справедливы для любого λ > 0).

Пусть j = 1. Запишем уравнения (8.6) для i = 1, 2, …, n – 1:

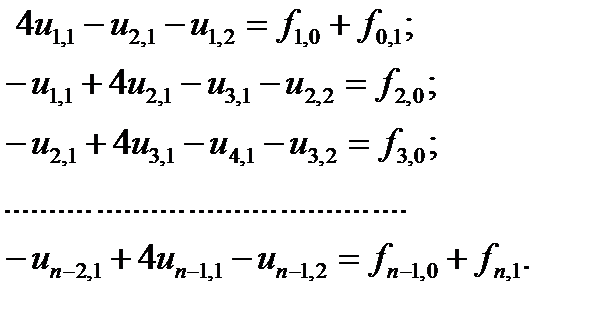
Увеличим j: j = 2. Снова запишем уравнения (8.6) для i = 1, 2, …, n – 1:

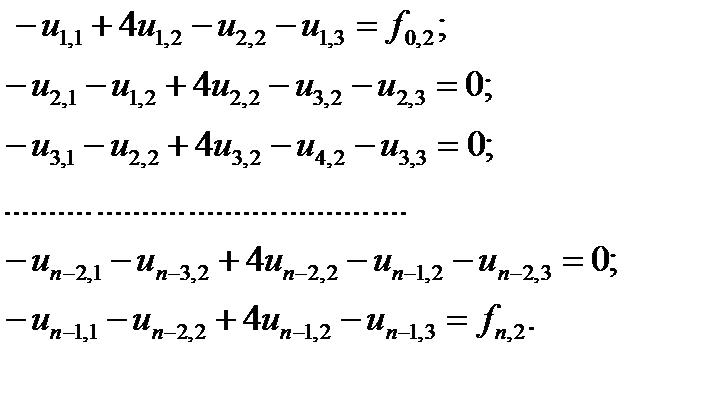
Продолжая и дальше увеличивать j (конечное значение будет равно m – 1) и проходя i = 1, 2, …, n – 1, получим систему уравнений.

Свойства полученной системы уравнений:

1. Подавляющая часть коэффициентов равна нулю.

2. В каждом уравнении есть коэффициент +4. Если всего ненулевых коэффициентов 5, то сумма остальных равна –4, иначе их сумма равна –2 или –3.

В системе выполнены условия сходимости итерационного метода Гаусса–Зейделя (второе свойство системы). Решение методом исключения переменных нецелесообразно (m и n могут быть порядка сотен).

Выпишем некоторые уравнения для итерационного процесса. Верхними индексами обозначим порядковый номер итерации и примем u⁽⁰⁾_i,j = 0 для всех i, j.

В каждом уравнении (начиная со второго) используется одно значение для текущей итерации, полученное из предыдущего уравнения. Остальные элементы берутся из предыдущей итерации.

Каждая пара i, j (j = 1, ..., m – 1; i = 1, ..., n – 1) определяет узел, в котором уравнение (8.6) решается относительно u_i,j.

Сравниваются значения, полученные на двух последовательных итерациях. Наибольшая разность значений сравнивается с допуском ε, т. е. проверяется, сошелся ли процесс.

Метод Гаусса–Зейделя в применении к эллиптическим разностным уравнениям называют методом Либмана или методом последовательных смещений.

Пока метод Либмана был рассмотрен только для случая уравнения Лапласа. Вообще говоря, любое эллиптическое уравнение без членов, содержащих u_xy, приводит к системе разностных уравнений, удовлетворяющих условиям сходимости.

Все сказанное до сих пор относилось к линейным уравнениям. Вопрос о сходимости для нелинейных уравнений разработан весьма слабо.

Имеется, однако, много успешных попыток решения квазилинейных уравнений с помощью экстраполированного метода Либмана.

Удавалось получить сходимость даже для уравнений с членом типа u_xy, хотя в этом случае нет никаких теоретических оснований ожидать сходимости.

8.2 ДУ в частных производных. Гиперболические уравнения

Напомним, что в общем случае мы имеем уравнение (8.1).

При B² – 4AC > 0 получаем уравнения гиперболического типа.

Типичный пример задачи – расчет колебаний струны.

Пусть имеется струна длиной L, натянутая между двумя точками оси х, точкой
х = 0 и точкой x = L. Натяжение струны равно Т. Если отклонить струну от положения равновесия и отпустить, то она начнет колебаться.

Смещение каждой точки струны относительно положения равновесия зависит не только от координаты x этой точки, но и от времени t (иллюстрация будет приведена ниже на рис. 8.4).

Отклонение струны от положения равновесия описывается уравнением гиперболического типа (его обычно называют волновым уравнением), которое приводится здесь без вывода:

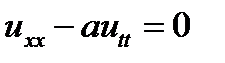
для 0 £ x £ L, t > 0.

Коэффициент а учитывает физические характеристики. Для простоты мы примем а = 1, так что задача выразится следующим образом:

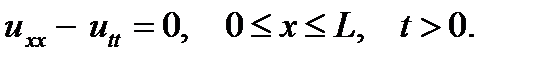(8.7)

Простая замена переменных сводит любое волновое уравнение к виду (8.7).

Поскольку концы струны закреплены, имеем

u(0, t) = u(L, t); t ³ 0.

(8.8)

Начальными условиями являются начальное смещение

u(x, 0) = f(x); 0 £ x £ L,

(8.9)

и начальная скорость

ut(x, 0) = g(x); 0 < x < L.

(8.10)

Возможные начальные условия задачи показаны на рис. 8.4.

Рис. 8.4. Иллюстрация к задаче о колебании струны. Показаны возможные начальные условия

Если мы оттянем струну за середину, как на рис. 8.4, и отпустим ее без придания ей начальной скорости, то начальные условия запишутся в виде

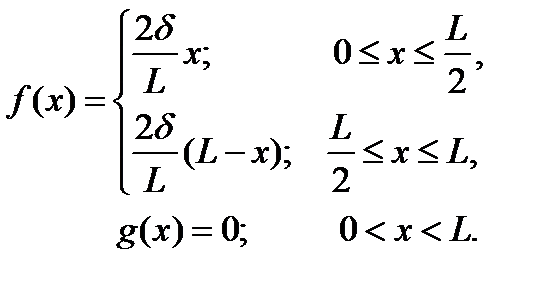
Мы назвали эти условия начальными, а не граничными. В действительности, если задать для гиперболического уравнения граничные условия, то полученная задача не будет иметь единственного решения.

Подобные задачи называются некорректно поставленными. Очень важно, чтобы дополнительные условия должным образом соответствовали каждому типу уравнений.

Чтобы найти разностные уравнения, соответствующие (8.7), воспользуемся равенствами (7.3) и (7.5), причем вместо у будем писать t. Теперь сетка простирается бесконечно в направлении положительных значений t – мы можем искать решение для сколь угодно далекого момента времени.

В направлении х примем шаг сетки равным h, в направлении t – равным k.

Интервал L разделяется на n = L/h малых интервалов h, а в направлении t может быть сколь угодно много интервалов k.

Если обозначить

u_i,j = u(ih, jk) и l = k/h,

то разностное уравнение запишется в виде

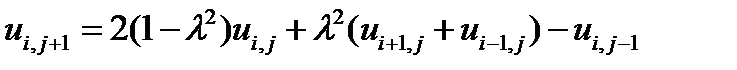(8.11)

для i = 1, 2, …, n и j = 1, 2, … .

Граничное условие (8.8) записывается в виде

u0, j = un, j = 0; j = 1, 2, 3, … .

(8.12)

Начальное условие (8.9) можно записать в виде

ui,0 = f(ih); i = 1, 2, … n – 1.

(8.13)

Для записи в разностном виде начального условия (8.10) можно использовать равенство (7.1), откуда

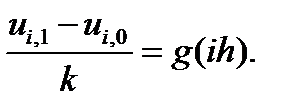
C помощью (8.13) получаем

ui,1 = f(ih) + kg(ih).

(8.14)