Модифицированный метод Эйлера

В исправленном методе Эйлера усреднялись наклоны касательных.

Можно пойти по другому пути и усреднять точки в следующем смысле.

На рис. 6.3 первоначальное построение проведено, как и прежде на рис. 6.2. (Прямая L₁ с тангенсом угла наклона f(x_m,y_m)).

Однако теперь берем точку, лежащую на пересечении L₁ и ординаты x = x_m+ h/2 (точка Р).

Рис. 6.3. Геометрическое представление модифицированного метода Эйлера

Найдем тангенс угла наклона касательной в точке P

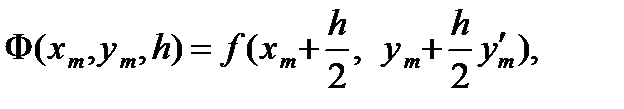(6.19)

где

.

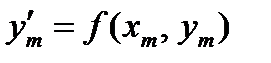Уравнение прямой L₀ можно записать в виде

y = y_m + (x – x_m)Ф(x_m, y_m, h),

где Ф задается формулой (6.19).

Поэтому можем записать

ym+1 = ym + hФ(xm, ym, h) .

(6.20)

Соотношения (6.19) – (6.20) описывают модифицированный метод Эйлера. Иногда его называют исправленным методом ломаных.

Этот метод тоже согласуется с разложением в ряд Тейлора вплоть до членов степени h², поэтому он тоже является методом Рунге–Кутты второго порядка.

Cравнение обоих рассмотренных методов

Оба метода описываются формулами вида

ym+1 = ym + hФ(xm, ym, h).

(6.21)

В обоих случаях Ф имеет вид

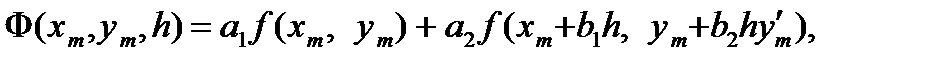
где 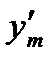= f(x_m,y_m).

В частности, для исправленного метода Эйлера

a₁ = a₂ = 1/2; b₁ = b₂ = 1 .

Для модифицированного метода Эйлера

a₁ = 0; a₂ = 1; b₁ = b₂ = 1/2.

Можно показать, что методы объединяются, если положить для обоих методов

a₂ = w¹ 0; a₁ = 1 – w; b₁ = b₂ = 1/(2w).

Ошибка ограничения равна e_T = Kh³.

Было показано, что наименьший верхний предел |K| достигается при w = 2/3.

Методы Рунге–Кутты

Рассмотрим метод Рунге–Кутты четвертого порядка – один из самых употребительных методов интегрирования дифференциальных уравнений.

Этот метод применяется настолько широко, что в литературе его часто называют «методом Рунге–Кутты» без всяких указаний на тип или порядок.

Итак, дано

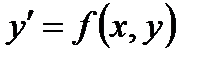(6.22)

с начальным условием 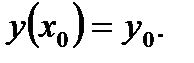Нужно найти решение уравнения (6.22) на отрезке [a, b].

Выбираем малый шаг h и на отрезке [a, b] строим систему равноотстоящих точек

.

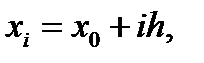
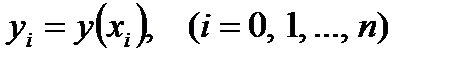Этот классический метод Рунге – Кутты описывается системой следующих пяти соотношений:

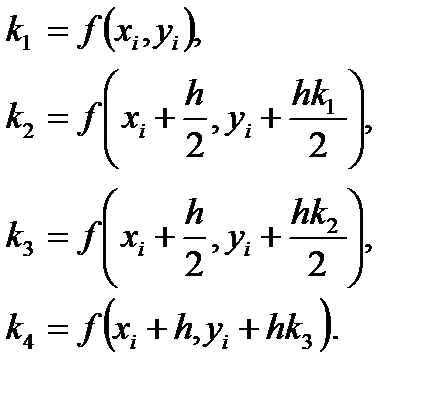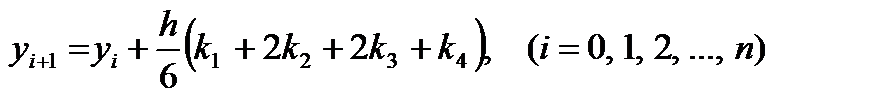(6.23)

Этому процессу можно дать геометрическую интерпретацию (рис. 6.4).

В точке (х_i, у_i)вычисляется тангенс угла наклона k₁; используя его, мы идем на половину шага вперед и находим тангенс угла наклона здесь.

Используя новый тангенс угла наклона k₂, мы опять начинаем из (х_i, у_i), идем вперед на половину шага и опять берем пробу тангенса угла наклона.

Взяв этот последний тангенс угла наклона k₃, мы опять начинаем из (х_i, у_i), но делаем теперь полный шаг вперед, где смотрим тангенс угла наклона k₄.

Четыре тангенса углов наклона усредняем с весами 1/6, 2/6, 2/6, 1/6 и, беря этот средний тангенс угла наклона, делаем окончательный шаг от (х_i, у_i)к (х_i+1, у_i+1).

Рис. 6.4. Иллюстрация к методу Рунге–Кутты 4-го порядка

Ошибка ограничения для этого метода равна e_T = Kh⁵, так что формулы (6.23) описывают метод четвертого порядка.

При использовании этого метода функцию необходимо вычислять четыре раза.

Можно показать, что классическая формула Рунге–Кутты оказывается обобщением формулы Симпсона для интегрирования функции одной переменной, причем обобщение состоит в том, что формула не ограничена теперь функциями только от х.

Пример

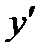= y; y(0) = 1.

Для этого уравнения из (6.23) получаем

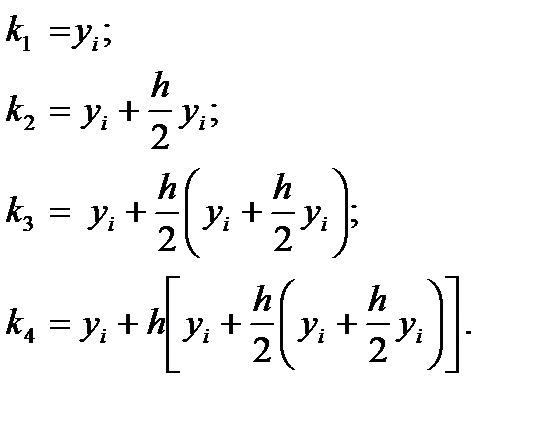
В результате получаем для y_i+1

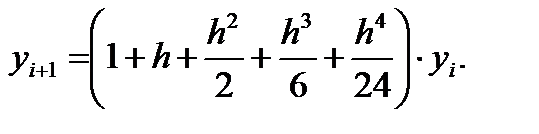
Сумма в скобках представляет собой теперь пять первых членов разложения функции e^h в ряд Тейлора.