Использование результатов и коррекция математической модели

Большинство полученных сначала результатов может оказаться бесполезным.

Часто анализ результатов на этапе их обработки и интерпретации, указывает на несовершенство используемой математической модели и необходимость ее коррекции.

В таком случае математическую модель модифицируют (при этом она, как правило, усложняется) и начинают новый цикл решения задачи.

Тема 1

Приближенные числа. Погрешности

1.0 Источники приближенных чисел

На практике при выполнении вычислений чаще всего приходится иметь дело не с точными, а с приближенными числами. Причин тому несколько.

Данные, значение которых в принципе может быть представлено целым числом, но точное его определение затруднительно. Например, поскольку число зрителей, пришедших на концерт, является целым, его можно было бы определить с абсолютной точностью, однако на практике это сделать довольно трудно.

Если в ходе вычислений используются экспериментальные данные, полученные из физических измерений или же наблюдений, то их значение не может быть измерено с абсолютной точностью. Даже использование весьма прецизионных (и дорогих!) измерительных приборов не позволяет достичь абсолютного результата.

В расчетах часто используются иррациональные величины (например, e, p), которые в принципе не имеют абсолютно точных значений.

Все сказанное справедливо для случая, когда имеется возможность выполнять вычисления с неограниченным числом знаков. Ситуация усугубляется при использовании вычислительной техники, поскольку всякий компьютер хранит вещественные числа с ограниченной точностью. Поясним сказанное внешне простым примером. Предположим, необходимо решить квадратное уравнение x² + 0,4002x + 0,00008 = 0 и вычисления производятся с точностью до 4-ой значащей цифры. С использованием обычной формулы

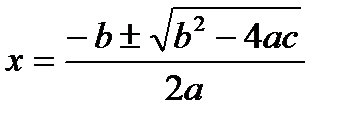
получаем один из корней –0,00015. При вычислениях с 8-ю значащими цифрами правильный корень равен –0,0002. Таким образом, в первоначальном варианте ошибка составила 25 %!

Приближенные числа – один из источников погрешностей, причины возникновения которых кратко рассмотрены в следующем параграфе.

1.1 Источники и классификация погрешностей

Обычно выделяют следующие источники погрешности решения задачи.

а) Математическое описание задачи является неточным. В частности, не удалось надлежащим образом описать задачу с помощью набора уравнений, неточно заданы исходные данные описания и др. Это неустранимая погрешность.

б) Применяемый для решения метод часто не является точным: получение точного решения задачи требует неограниченного или неприемлемо большого числа арифметических операций, поэтому вместо получения точного решения приходится прибегать к приближенному. Это погрешность метода.

в) При выполнении арифметических операций на компьютере или любым другим образом, как правило, производятся округления (это же относится к вводу чисел в память компьютера и выводу полученных результатов). Это вычислительная погрешность.

1.2 Абсолютная и относительная погрешности вычисления

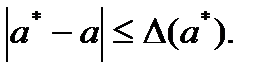
Если a – точное значение некоторой величины, а a* – известное приближение к нему, то абсолютной погрешностью приближения a* называют величину Δ(a*), удовлетворяющую неравенству

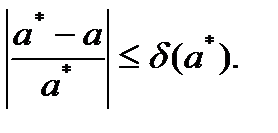
Относительной погрешностью называют величину d (a*), удовлетворяющую неравенству

Относительную погрешность часто выражают в процентах.

Рассмотрим способы нахождения погрешностей результата при выполнении арифметических операций.

Пусть X и Y – «точные» значения двух величин. В вычислительном устройстве (после округления) они представлены как x и y.

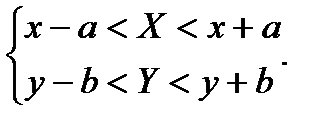
Можно записать

Здесь a и b – положительные числа.

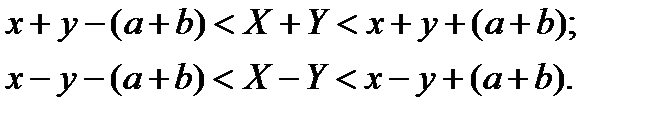
Очевидно, что

Вывод: при сложении (вычитании) двух чисел максимальная погрешность суммы (разности) равна сумме максимальных погрешностей исходных двух чисел.

Рассмотрим теперь случаи произведения и деления приближенных величин.

Перепишем соотношения

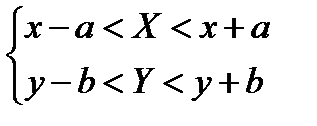
в виде

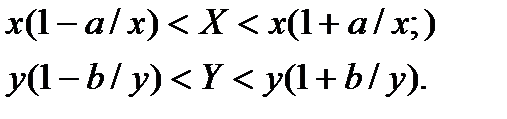
Пренебрегая малыми величинами (a/x)(b/y), получаем для XY

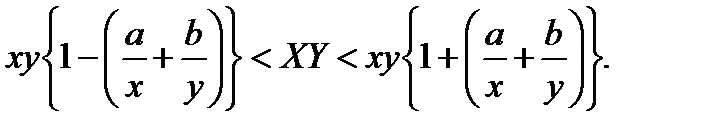
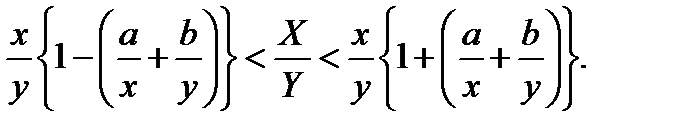
Для частного находим

Вывод: при умножении (делении) двух чисел максимальная относительная погрешность произведения (частного) равна сумме максимальных относительных погрешностей исходных двух чисел.

Представим сказанное в несколько более формализованном виде.

1.3 Погрешности арифметических операций

Погрешность суммы

Пусть задана функция

Для абсолютной погрешности получаем

Относительная погрешность

Погрешность разности

Пусть задана функция

Для абсолютной погрешности получаем

Относительная погрешность

Если и близки, относительная погрешность может оказаться много больше и .

Погрешность произведения

Пусть задана функция

Для абсолютной погрешности получаем

Относительная погрешность

Погрешность частного

Пусть задана функция

Для абсолютной погрешности получаем

Относительная погрешность

1.4 Обратная задача теории погрешностей

Рассмотренные выше оценки относились к «Прямой задаче погрешностей» – т. е. нахождению погрешности функции по погрешностям аргументов.

Обратная задача теории погрешностей – нахождение допустимой погрешности аргументов, при которой погрешность значений функции будет не более заданной величины e.

В общем случае обратная задача математически некорректна. Возможно, однако, рассмотрение некоторых частных случаев.

В рассмотрении используем неравенство

Накладывается условие .

Рассмотрим три частных случая.

I. Если функция зависит от одной переменной, т. е. n = 1, то .

II. При n > 1 если погрешности переменных одинаковы, D(x₁ ) = … = D (x_i ) = D, то .

III. При n > 1, если вклады в погрешность результата одинаковы,

, то .

Тема 2

Решение алгебраических
и трансцендентных уравнений

Необходимость решения уравнений возникает при рассмотрении большого числа разнообразных задач. При этом зачастую приходится прибегать к численным методам, поскольку даже в случае алгебраических уравнений порядка n общие решения найдены лишь для n < 5. Что касается трансцендентных уравнений, то общие решения, как правило, отсутствуют вовсе.

2.0 Постановка задачи

В общем случае задача имеет вид

(2.1)

где f(x) – заданная функция действительного или комплексного аргумента x.

Корнем (или решением) уравнения (2.1) называется значение c, при котором f(c) = 0.

Приближенное нахождение корней уравнения складывается из двух этапов:

отделение корней, т. е. нахождение наиболее узких интервалов [a, b], в каждом из которых содержится один и только один корень данного уравнения (количество интервалов определяется видом функции f(x));

1) уточнение приближенных корней, т. е. вычисление корней с заданной степенью точности.

Для отделения корней чаще всего применяют графический метод, основанный на том, что вещественные корни уравнения (2.1) являются точками пересечения графика функции f(x) с осью x. Следовательно, построив график, можно принять за приближенные значения корней абсциссы точек пересечения графика с осью x.

Иногда удобно функцию f(x) представить в виде f₁(x) = f₂(x), построить графики y = f₁(x)
и y = f₂(x) и найти абсциссы их точек пересечения. Эти точки и будут приближенными значениями корней.

Пример

Отделить корни уравнения x² + x – 2 = 0.

Можно построить график функции x² + x – 2 = 0. Точки пересечения этого графика с осью x будут являться приближенными корнями уравнения (рис. 2.1).

Кроме того, можно исходное уравнение записать в виде x² = 2 - x и построить графики y = x² и y = 2 - x. Абсциссы точек пересечения этих графиков можно принять за приближенные корни заданного уравнения (рис. 2.2).

x2+x - 2	x2 2-x
Рис. 2.1. График функции x2 + x – 2	Рис. 2.2. Графики функций x2 и 2 – x

Еще один способ отделения корней: исследование функции f(x) для установления интервалов, на которых происходит изменение знака функции (рис. 2.3).

Рис. 2.3. Интервал [a, b], на концах которого функция принимает разные знаки

Приведенная на рис. 2.3 ситуация может показаться самоочевидной, однако на практике попадаются гораздо более сложные случаи (рис. 2.4–2.6).

Рис. 2.4. На концах всех интервалов
функция имеет одинаковые знаки, однако
на интервале [a, b] имеются два корня, на интервале [c, d] – один корень, на интервале [e, f] корней нет

Рис. 2.5. «Патологическая» функция,
многократно проходящая через 0 на небольшом интервале

Рис. 2.6. Разрывная функция,
принимающая на концах интервала [a, b] разные знаки, однако внутри интервала корней нет!

Очень полезной оказывается следующая теорема.

Теорема: Пусть функция f(x) непрерывна на интервале [a, b] и принимает на концах данного интервала значения разных знаков, т. е. f(a)f(b) < 0.

Тогда внутри интервала [a, b] найдется такая точка c, значение функции в которой равно нулю, т. е. f(c) = 0, и которая является корнем данного уравнения.

Корень c заведомо будет единственным на [a, b], если производная существует и сохраняет постоянный знак внутри данного интервала, т. е. если или .

Численные методы, используемые для уточнения приближенных корней, применяются для каждого найденного интервала заданного уравнения.

2.1 Метод половинного деления (метод «вилки», метод дихотомии)

Определяем, какие корни требуется найти, например, только положительные или только отрицательные и т. д.

Графическим методом находим интервалы, в каждом из которых находится только один корень данного уравнения.

Разделим отрезок [a, b] пополам точкой d и получим уже два интервала: [a, d] и [d, b].

Выбираем тот отрезок, на концах которого функция f(x) принимает значения разных знаков,
и опять делим его пополам.

Повторяем все эти действия до тех пор, пока длина отрезка, содержащего корень, не станет меньше погрешности, с которой ищется корень.

Легко видеть, что после N делений длина отрезка уменьшится в 2^N раз. Так, после 20-ти делений длина отрезка составит 1/2²⁰ долю от первоначальной, т. е. уменьшится в 1 048 576 раз.

Пример

Методом половинного деления найти корень уравнения .

Графически находим интервал [0,4; 0,5], в котором находится действительный корень данного уравнения.

f(0,4) = –0,136 < 0;

f(0,5) = 0,125 > 0.

Условие нахождения корня в рассматриваемом интервале выполняется,
т. е. f(0,4)f(0,5) < 0.

Интервал [0,4; 0,5] делим пополам точкой = 0,45. Получаем два интервала: [0,4; 0,45] и [0,45; 0,5].

Для того чтобы определить, в каком из полученных интервалов содержится искомый корень уравнения, проверим условие < 0.

f(0,4) = –0,136 < 0;

f(0,5) = 0,125 > 0;

f(0,45) = –0,00888 < 0.

< 0, следовательно, выбираем [0,45; 0,5]. Этот интервал делим пополам:

= 0,475.

Опять получаем два интервала: [0,45; 0,475] и [0,475; 0,5].

f(0,475) = 0,05717 > 0.

Т. к. < 0, то выбираем [0,45; 0,475].

Так продолжаем до тех пор, пока не найдем корень данного уравнения.

.................................

[0,453397; 0,4534];

= 0,453398;

f(0,453398) = 0,0000009.

Очевидно, что x = 0,453398 является искомым корнем данного уравнения с довольно высокой точностью.

2.2 Метод Ньютона (метод касательных)

Основное достоинство метода – быстрая сходимость.

Метод Ньютона универсален и пригоден для решения обширного класса уравнений.

Пусть корень с уравнения f(x) = 0 принадлежит отрезку [a, b], причем, , и непрерывны и сохраняют определенные знаки на данном отрезке.

Метод имеет простой геометрический смысл.

Если x₀ – некоторое приближение к корню с уравнения, то за новое приближение x₁ принимают точку пересечения касательной, проведенной в точке (x₀, f(x₀)) к графику функции f(x), с осью Ox (рис. 2.7).

α

Рис. 2.7. Иллюстрация выбора следующего приближения к корню уравнения
в методе Ньютона

Алгоритм поиска корня задает итерационная формула:

(2.2)

Каждое последующее приближение к корню вычисляется через предыдущее.

При неудачном выборе x₀ может случиться, что следующее приближение x₁ к корню уравнения окажется вне интервала [a, b]. При этом надо выбрать другое начальное приближение.

В противном случае метод Ньютона может сходиться очень медленно, что приведет к накоплению погрешности вычисления, или не сходиться вообще.

Применяя метод Ньютона, следует руководствоваться следующим правилом при выборе начальной точки: в качестве начального приближения x₀ выбирается тот конец интервала
[a, b], которому отвечает ордината того же знака, что и знак , т. е. должно выполняться условие > 0 (на концах интервала).

Если > 0, то принимаем x₀ = a, если > 0, то x₀ = b.

Замечание

Недостатком метода Ньютона является необходимость вычисления производной для каждого x_n. Если значение производной близко к нулю, то новое приближение x_n+1 может быть худшим приближением, чем x_n.

Иногда целесообразно применять модифицированный метод Ньютона, в котором последовательные приближения определяются формулой

Формула весьма полезна, если вычисление сложно. С другой стороны, модифицированный метод сходится значительно медленнее, чем основной метод Ньютона.

Пример

Методом Ньютона (касательных) вычислить корни уравнения .

Графически находим два интервала [–1,4; –1,3] и [0,5; 0,6]. Сразу найдем корень, принадлежащий [–1,4; –1,3].

f(–1,4) = 0,20660 > 0,

f(–1,3) = –0,03747 < 0.

f(–1,4) f(–1,3) < 0, следовательно, корень находится в этом интервале.

Корень будем уточнять по формуле .

За начальное приближение x₀ принимаем тот конец интервала [–1,4; –1,3], для которого выполняется условие > 0.

, .

= 2,27253 > 0, = 2,24660 > 0.

Для точки x = –1,4 выполняется условие > 0, поэтому положим
x₀ = –1,4.

= –1,31909;

= –1,31598;

= –1,31597; = –1,31597.

Один корень уравнения x = –1,31597.

Все в том же порядке повторим для интервала [0,5; 0,6].

f(0,5) = –0,10128 < 0,

f(0,6) = 0,18212 > 0.

< 0, следовательно, корень находится в этом интервале.

Для уточнения корня опять воспользуемся формулой .

За начальное приближение принимаем тот конец интервала [0,5; 0,6], для которого выполняется условие > 0.

Т.к. для точки x = 0,6 выполняется условие > 0, то положим x₀ = 0,6.

Проделав выкладки, аналогичные предыдущим, получим x = 0,53727.

Отметим, что при использовании метода Ньютона возможна ситуация «зацикливания», особенно, если функция f(x)получена с помощью интерполяции (рис. 2.8). Спасает дело лучший выбор начального приближения.

Рис. 2.8. «Зацикливание» итераций в методе Ньютона, поскольку касательные
в точках 1 и 2 оказались параллельны

2.3 Метод хорд (метод пропорциональных частей)

Пусть корень с уравнения f(x)= 0 принадлежит отрезку [a, b], причем производные и непрерывны и сохраняют определенные знаки на данном отрезке.

Сначала изучается расположение корней и осуществляется их отделение. Затем выбирается начальное приближение x₀.

Правильный выбор начального приближения x₀ влияет на сходимость метода.

При неправильном выборе x₀ каждое следующее приближение может все дальше удаляться от корня уравнения, т. е. метод хорд будет расходиться.

Применяют следующее правило выбора начального приближения: неподвижен тот конец интервала [a, b], для которого знак функции f(x) совпадает со знаком ее второй производной , т. е. должно выполняться условие f (x) > 0.

Если > 0, то точка a является неподвижной, а в качестве начального приближения выбираем точку b, т. е. x₀ = b, и формула, определяющая алгоритм вычислений, имеет вид

В обратном случае

Метод проиллюстрирован на рис. 2.9. После отделения корня через точки 1 и 2 проводим хорду и находим точку ее пересечения с осью абсцисс. В этой точке восстанавливаем перпендикуляр до пересечения с кривой. Тем самым находим точку 3. Через точки 2 и 3 проводим новую хорду до пересечения с осью Ox. Из точки пересечения снова восстанавливаем перпендикуляр до пересечения с кривой. Получаем точку 4. Процесс продолжается до достижения необходимой точности.

Рис. 2.9. Иллюстрация к методу хорд. Точки 1 и 2 получены при отделении корня. Все последующие – в ходе применения процедуры метода хорд

Пример.

Методом хорд найти корни уравнения

Построив график функции , находим, что данное уравнение имеет один действительный корень, лежащий в интервале [1,4; 1,5].

0,0

0,5

1,0

1,5

2,0

2,5

y

x

y=2x*ln(x)-1

Проверим условие нахождения корня в данном интервале

f(1,4) = – 0,05788 < 0, f(1,5) = 0,21640 > 0.

f(1,4) f(1,5) < 0, следовательно, условие нахождения корня в найденном интервале выполняется.

Далее найдем .

= 1,42857 > 0, = 1,33333 > 0.

Определим неподвижную точку согласно условию > 0. Так как > 0, то точка = 1,5 является неподвижной, а в качестве начального приближения корня выбираем точку = 1,4.

Каждое (n+1) приближение корня вычисляем по формуле .

= 1,42152;

= 1,42153, = 1,42153.

Сравнивая и , видим, что корнем уравнения является число = 1,42153.

Возможны случаи, когда метод хорд будет сходиться крайне медленно. Одна из возможных ситуаций проиллюстрирована на рис. 2.10.

Рис. 2.10. Пример функции, для которой метод хорд сходится очень медленно

2.4 Метод итерации (метод последовательных приближений)

Метод универсален: его можно применять для решения обширного класса как линейных, так и нелинейных уравнений.

Сущность метода в следующем.

Пусть дано уравнение f(x)= 0, где f(x) – непрерывная функция, и требуется найти его вещественные корни.

Преобразуем уравнение в эквивалентное уравнение вида

.

(2.3)

Выберем начальное приближение x₀ и, подставив его в правую часть уравнения (1.3), получим число x₁ = j(x₀ ). Затем вычислим x₂ = j(x₁ ) и т. д.

Получим последовательность чисел , определяемую равенством

(2.4)

Для того чтобы последовательность сходилась к корню с уравнения f(x) = 0, необходимо выполнение условия сходимости: если функция j(x) определена и дифференцируема на отрезке [a, b]и при всех a < x < b, то процесс итерации (2.4) сходится к корню с уравнения f(x) = 0 независимо от начального значения x₀Î [a, b].

Условие сходимости имеет вид

,

(2.5)

где q – максимальное значение производной на интервале, содержащем корень уравнения (если корней несколько, то условие сходимости должно выполняться для каждого интервала).

Чем ближе к нулю максимальное значение производной q, тем выше скорость сходимости метода.

Замечание

Пусть в некоторой окрестности [a, b] корня с уравнения x = j(x) производная сохраняет постоянный знак и выполнено неравенство .

Тогда, если производная положительна, т. е. , то последовательные приближения

x₀Î [a, b] сходятся к корню монотонно.

Если же производная отрицательна, то последовательные приближения колеблются около корня с.

Для метода итерации большое значение имеет способ преобразования уравнения (2.1) к виду (2.3), т. е. выбор функции , которая должна подчиняться условию сходимости .

Есть достаточно общий прием приведения уравнения (2.1) к виду (2.3), для которого обеспечено выполнение неравенства (2.5).

Пусть искомый корень лежит в интервале [a, b], причем

для xÎ [a, b], где m – наименьшее значение, а M – наибольшее значение производной на [a, b].

Если производная отрицательна, то вместо уравнения f(x) = 0 рассматриваем уравнение
– f(x) = 0.

Введя множитель , произведем простые преобразования:

.

В итоге заменим уравнение (2.3) эквивалентным уравнением вида

(2.7)

Сравнивая (2.7) и (2.3), видим, что j(x) = x – lf(x).

Поскольку метод итерации должен быть сходящимся и для функции j(x) должно выполняться условие (2.5), то будем иметь

.

(2.8)

Можно положить:

(2.9)

Фактически выражения (2.7), (2.9) дают универсальный способ нахождения функции j(x), т. е. универсальный способ приведения уравнения (2.1) к виду, пригодному для запуска итерационной процедуры.

В методе итерации в качестве начального приближения x₀ чаще всего принимается один из концов интервала [a, b]. Если e – точность, с которой необходимо найти корень, то выход из процедуры происходит обычно по условию

где x⁽ⁿ⁾и x^(n-1) – приближенные значения корня, соответственно, на n-ой и (n–1)-ой итерациях.

Замечание

Преимущество метода итерации заключается в том, что сходимость процесса не зависит от выбора начального приближения x₀.

Отдельная ошибка, допущенная при вычислениях, не выводящая за пределы отрезка [a, b], не повлияет на конечный результат.

Такое свойство называют свойством самоисправляемости сходящегося итерационного процесса.

На рис. 2.11 показано, как «работает» метод итераций в случае «хороших» функций j(x), т. е. когда

На рисунках отложены прямая y = x и кривая y = j(x). Корень уравнения отвечает абсциссе точки пересечения этих двух линий.

После выбора начального приближения x₀ вычисляется значение функции j(x₀)– ему соответствует точка А на рис. 2.11а.

Приравнивание x₁ = j(x₀)означает, что мы проводим через точку А прямую, параллельную оси абсцисс, до пересечения с прямой y = x (точка В). Получаем новую абсциссу x₁. С ее использованием вычисляем новое значение функции j(x₁)(точка С на рис. 2.11а).

Процедура повторяется до нахождения корня с заданной точностью.

На рис. 2.11 показаны также монотонная сходимость к корню и осцилляции вокруг него.

На рис. 2.12 проиллюстрировано поведение итерационной процедуры, когда условие (2.5) не выполняется. По аналогии с рис. 2.11 можно видеть монотонное и осциллирующее удаление приближенных решений от корня уравнения.

а	б
Рис. 2.11. «Работа» метода итераций в случае «хороших» функций j(x): а – ; б –

а	б
Рис. 2.12. Расходимость метода итераций в случае : а – ; б –

В заключение темы рассмотрим пример использования техники, задаваемой выражениями (2.7), (2.9).

Пример

Методом итерации решить уравнение .

Построив график функции, находим, что уравнение имеет единственный действительный корень, принадлежащий отрезку [1,1; 1,2].

Преобразуем данное уравнение к виду (2.3) следующим образом: . При таком преобразовании имеем .

Проверим выполнение условия сходимости (2.5).

.

>1;

>1.

Видно, что условие сходимости (2.5) не выполняется и такое преобразование не подходит, т. к. метод будет расходиться.

Преобразуем уравнение к виду (см. (2.7))

x = x – l(x⁵ + x – 3).

Согласно (2.9), l= 1/M, где М – наибольшее значение производной на отрезке.

= 5x⁴ + 1.

= 8,3205;

= 11,368.

Таким образом, l = 1/11,368 и

.

В качестве нулевого приближения выберем среднюю точку отрезка x₀ = 1,15.

Тогда

x₁ = 1,12547; x₂ =1,13152; x₃ = 1,13272; x₄ = 1,13294;

x₅ = 1,13299; x₆ = 1,13300; x₇ = 1,13300.

Тема 3

Решение систем
линейных и нелинейных уравнений

3.0. Постановка задачи

Рассмотрим систему линейных уравнений

(3.1)

Решением системы (3.1) называется совокупность таких значений неизвестных

(3.2)

при которых каждое из уравнений этой системы обращается в тождество.

Систему (3.1) кратко можно записать в виде матричного уравнения

.

(3.3)

Если определитель матрицы А не равен нулю (матрица неособенная), то решение системы (3.3) существует и оно единственное.

Имеется два основных метода «не численного» решения линейных систем: метод Гаусса и метод Крамера. С вычислительной точки зрения они сильно отличаются друг от друга по числу умножений и делений, которые необходимо выполнить в процессе решения. От этого, в свою очередь, зависит время, затрачиваемое на вычисления. Зависимость числа названных операций N от порядка системы (n) для двух упомянутых методов приведена в табл. 3.1.

Таблица 3.1 Число операций умножения и деления N для некоторых порядков n системы линейных уравнений

n	N по Крамеру	N по Гауссу
	~3,6 ∙108
	~7,6 ∙1067	44 150

Если преобразовать систему (3.1) к специальному виду, ее можно решить методом итерации.

3.

3.0

3.1 Решение систем линейных уравнений методом итерации

Прежде всего, надо проверить выполнение условий сходимости метода.

Для того чтобы метод итерации сходился, необходимо, чтобы выполнялось условие сходимости для системы (3.1): метод итерации сходится, если выполнены неравенства

> (i = 1, 2, ..., n),

(3.4)

т. е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов, не считая свободных членов.

Преобразуем систему (3.1) к специальному виду: разрешим первое уравнение системы относительно x₁, второе – относительно x₂ и т. д.

В результате получим эквивалентную систему

(3.5)

Введя обозначения при и , при ,

представим систему (3.5) в виде

(3.6)

Перепишем систему в матричной форме:

.

(3.7)

Здесь a – матрица с нулевыми диагональными элементами. В качестве начального приближения

можно принять столбец свободных членов

Матрицу X⁽⁰⁾ подставляем в правую часть системы (3.6)