Области применения функций распределения каждого из названных видов функций
Область применения Закона Парето:Вилфредо Парето изначально использовал это распределение для описания распределения благосостояния, а также распределения дохода. Его правило 20 к 80 (которое гласит: 20% популяции владеет 80% богатства) однако зависит от конкретной величины k, и утверждается, что фактически встречаются существенные количественные отклонения, например, данные самого Парето по Британии в Cours d'économie politique говорят, что там примерно 30% населения владеет 70% общего дохода.
Распределение Парето встречается не только в экономике. Можно привести следующие примеры:
· В лингвистике распределение Парето известно под именем закона Ципфа (для разных языков показатель степени может несколько различаться, также существует небольшое отклонение от простой степенной зависимости у самых частотных слов, однако в целом степенной закон описывает это распределение достаточно хорошо). Частными проявлениями этой закономерности можно считать:
· Зависимость абсолютной частоты слов (сколько всего раз каждое конкретное слово встретилось) в достаточно длинном тексте от ранга (порядкового номера при упорядочении слов по абсолютной частоте). Степенной характер остается вне зависимости от того, приводятся ли слова к начальной форме или берутся из текста как есть.
· Аналогичная кривая для популярности имен.
· Распределение размера населенных пунктов.
· Распределение размера файла в интернет-трафике по TCP-протоколу.
Область применения равномерного закона распределения:равномерное распределение используется как базовое для генерации псевдослучайных чисел.
Простейший пример дискретного равномерного распределения можно наблюдать, бросая кубик или монетку.
Область применения экспоненциального закона распределения вероятностей:
Экспоненциальное (показательное) распределение часто встречается в теории массового обслуживания (например, X — время ожидания при техническом обслуживании или X — продолжительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и теории надёжности (например, X — срок службы радиоэлектронной аппаратуры).
Область применения закона Пуассона: непонятно зачем выделили У вас было наименование закона с одной буквой с!
применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина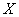 
распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
Область применения нормального закона распределения или распределение Гаусса:
Закон нормального распределения, так называемый Закон Гаусса, - один из самых распространенных законов Это фундаментальный закон в теории вероятностей и в ее применении. Нормальное распределение часто встречается в изучении природных и социально-экономических явлений. Иначе говоря, большинство статистических совокупностей в природе и обществе подчиняется закону нормального распределения Соответственно можно сказать, что совокупности значительной части больших по объему выборок подчиняются закону нормального распределения Те из совокупностей, которые отклоняются от нормального распределения в результате специальных преобразований могут быть приближены к нормальному В связи с этим следует помнить, что принципиальная особенность этого закона применительно к другим законам распределения заключается в том, что он является законом границы, к которой приближается (-аються) другие законы распределения в определенных (типовых) условиях.?
Почему в этой копии файла из сети нет знаков препинания?
Список литературы:
1) http://bibliofond.ru/view.aspx?id=526336
2) http://www.km.ru/referats/2C081520B6A8458B89382BBB274FD151
3) http://www.bestreferat.ru/referat-56860.html
4) https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B2%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9
5) http://zyurvas.narod.ru/knigi/Volkovec.pdf
6) http://stu.alnam.ru/book_om.php?id=38
7) http://risktheory.novosyolov.com/distr_handbook.htm
8) http://edu.tltsu.ru/er/book_view.php?book_id=1cee&page_id=19506
9) http://studopedia.org/1-39812.html
10) http://www.matburo.ru/tv_spr_sub.php?p=3
11) https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%9F%D0%B0%D1%80%D0%B5%D1%82%D0%BE
12) http://rdostudio.raox.ru/help/help/rdo_lang_rus/html/rdo_theory/rdo_theory_seq_uniform.htm
13) http://mathhelpplanet.com/static.php?p=osnovnye-zakony-raspredeleniya-nepreryvnyh-sluchainyh-velichin
14) http://sernam.ru/book_tp.php?id=24
15) https://uchebnikionline.com/statistika/statistika_-_oprya_at/normalniy_rozpodil-1.htm
{\displaystyle f_{X}(x)=\left\{{\begin{matrix}{\frac {kx_{m}^{k}}{x^{k+1}}},&x\geq x_{m}\\0,&x<x_{m}\end{matrix}}\right..}