Метод динамического программирования. Принцип оптимальности Беллмана

Источник: http://statistica.ru/branches-maths/printsip-optimalnosti-bellmana

Принцип оптимальности Беллмана позволяет решать или осмыслить многие интересные задачи, возникающие в реальной жизни, например, задачу о рациональной эксплуатации генерирующего предприятия (ТЭЦ, ГЭС), выбора экономичного состава агрегатов и др.

При эксплуатации гидростанций и тепловых станций возникает необходимость периодической остановки агрегатов при снижении нагрузки и включения агрегатов, находящихся в резерве, когда нагрузка увеличивается. Включение в работу определенных агрегатов влияет на величину и размещение резервов системы, на режим электрической сети, на перетоки по межсистемным линиям электропередачи, на расход топлива и тд.

Если на станциях имеется n агрегатов и каждый из них может быть либо включен, либо отключен, то все множество всех вариантов для работы с любой мощностью составит 2 в степени n.

Даже для n = 50 число вариантов становится очень большим!

В общем виде такие задачи являются нелинейными, целочисленными, многоэкстремальными, на состав агрегатов влияет режим электрических сетей, который следует оценивать и прогнозировать статистическими методами. Для решения таких задач обычный математический аппарат не подходит.

В частном случае методы динамического программирования позволяют решать подобные задачи при числе агрегатов порядка 20-30.

Приведем примеры задач, в которых принцип динамического программирования эффективно работает и позволяет найти оптимальное решение.

Задача о графике эксплуатации электростанция. Станция имеет L агрегатов, известна производительность одного агрегата и цена единицы произведенной электроэнергии.

Задан график оплаченной электроэнергии, избыточно произведенная электроэнергия не оплачивается.

Известны затраты на поддержание в рабочем агрегатов, затраты на консервацию и затраты на пуск. Требуется определить оптимальный режим эксплуатации.

Интересны задачи о распределении инвестиций и ресурсов.

Задача о распределении инвестиций: имеется несколько предприятий, между которыми требуется распределить данную сумму инвестиций. Известна эффективность вложения данной суммы средств в каждое предприятие.

Задача о распределении ресурса: имеется N предприятий, каждое из которых приносит доход, зависящий от доли выделенного ресурса. Требуется наилучшим способом распределить между ними ограниченный ресурс a на доли x1, ... , xN (x1 ≥ 0, ... , xN ≥ 0, x1 +...+ xN ≤ a).

Задача о наилучшей загрузке транспорта: транспорт, имеющее грузоподъемность a , загружается грузами N типов. Каждый тип груза имеет стоимость yi и вес zi .

Требуется найти оптимальный вариант загрузки, при котором стоимость взятых на борт предметов максимальна.

Задача о замене автомобиля: автотранспортное предприятие планирует приобрести автомобиль и эксплуатировать его в течение N лет.

Можно либо купить новый автомобиль возраста x0 = 0 лет и стоимости p, либо бывший в эксплуатации возраста 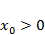лет по стоимости, зависящей от времени эксплуатации.

Показатели эксплуатации автомобиля включают: f (t) – стоимость произведенных за год изделий на оборудовании возраста t лет; r(t) – затраты на эксплуатацию в течение года автомобиля возраста t.

В процессе эксплуатации автомобиль можно продавать по ликвидной стоимости и купить новый. В конце срока эксплуатации автомобиль также продается по ликвидной стоимости. Определить оптимальный возраст автомобиля при покупке и оптимальный график его замены.

Все эти и многие другие задачи могут быть решены с помощью принципа оптимальности Беллмана.

Опишем формально принцип Беллмана и объясним его смысл.

Ключевым является понятие управляемого объекта, к которому применяется принцип Беллмана.

Пусть имеется изменяющийся во времени объект, на который осуществляется внешнее воздействие u(t) или управление, а x(t) – описание этого объекта в момент времени t.

Если при известном управлении до момента t1, зная описание x(t) в момент времени t , можно однозначно определить его значение x(t) для любого t > t1 , то такое описание называют полным.

Полное описание называют состоянием, множество возможных состояний – пространством состояний.

Сам объект, допускающий возможность полного описания, называют динамической системой.

Будем рассматривать только дискретные моменты времени и в эти моменты управлять системой.

Каждому переходу из состояния xk в следующее состояние ставится в соответствие функция затрат, зависящая от состояния xk , момента времени и применяемого управления.

Требуется найти такое начальное состояние и такой допустимый набор управлений, переводящий систему в одно из конечных состояний, чтобы общие затраты, являющиеся аддитивной функцией затрат на отдельных шагах, были минимальны.

Итак, на каждом шаге мы вносим плату за выбранное управление, далее плата, внесенная на каждом шаге, суммируется и подводится итог.

Мы желаем таким образом управлять объектом, чтобы общая сумма затрат была минимальной.

Это и есть общая постановка задачи динамического программирования или управления динамической системой.

Иными словами, нам нужна программа действий на каждом шаге, позволяющий минимизировать затраты.

Общий принцип формулируется так: вне зависимости от того, каким образом управляемый процесс на шаге k попал в состояние xk , далее надо применять управление, оптимальное для этого состояния в завершающем (N − k)-шаговом процессе с учетом оптимального продолжения.

Это одна из возможных формулировок принципа Беллмана в форме достаточного условия.

Пусть Yk – множество состояний, из которых (при использовании допустимых управлений) можно ровно за k шагов попасть в одно из состояний финального множества X N.

Можно считать, что Y0 = X N.

Возьмем произвольное xN −k ∈Yk и обозначим через Sk (xN −k ) функцию, описывающую зависимость оптимальных затрат от состояния xN −k за k последних шагов, переводящих систему из xN −k в X N.

Такие функции называют функциями Беллмана.

Поскольку для состояний xN −1 из множества Y1 переход в XN происходит за один шаг, то функция оптимальных затрат S1(xN −1) может быть записана следующим образом:

S1(xN−1) = min{dN (xN−1, uN )} (1)

uN ∈ UN (xN−1)

fN (xN−1, uN) ∈X N

Второе ограничение необходимо для того, чтобы гарантировать достижение заданного финального множества X N.

Значение uN , при котором достигается минимум в этом соотношении, обозначим через u*N( xN-1).

Несложно понять (сделайте это!), что функция оптимальных затрат Sk +1(xN −k −1) каждой следующей задачи рекуррентно выражается через предыдущую Sk (xN −k )

Sk+1 (xN−k−1) = min {dN−k (xN−k−1, uN−k )+ Sk ( fN−k (xN−k−1, uN−k ))} (2)

u*N −k (xN −k – 1) – управление, при котором достигается минимум затрат в (2).

Выражение u*k (xk-1) − определяет для каждого момента времени оптимальные правила управления в виде функций от текущего состояния динамического процесса, задают закон оптимального управления в форме оптимального регулятора по состоянию.

Оптимальное начальное состояние x*0 можно получить из решения следующей задачи:

x*0 = argmin (SN( x0), x0 ∈ X0) (3)

Систему (1)-(3) называют рекуррентными уравнениями Беллмана.

Значения оптимального управления в явном виде можно последовательно определить следующим образом:

Стартуем из начального состояния x0.

Шаг 1.

u*1 = u*1( x0)

x*1 = f1(x*0, u*1)

Шаг 2.

u*2 = u*2( x1)

x*2 = f2(x*1, u*2) и т.д.