Глава 3. Предпосылки метода наименьших квадратов

При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей .В модели

Случайная составляющая представляет собой ненаблюдаемую величину. После того как произведена оценка параметров модели, рассчитывая разности фактических и теоретических значений результативного признака у, можно определить оценки случайной составляющей у- . Поскольку они не есть реальные случайные остатки, их можно считать некоторой выборочной реализацией неизвестного остатка заданного уравнения, т. е. .

При изменении спецификации модели, добавлении в нее новых наблюдений выборочные оценки остатков могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений 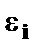, т. е. остаточных величин.

В предыдущих разделах мы останавливались на формальных проверках статистической достоверности коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента, F-критерия Фишера и Z-преобразования (для коэффициентов корреляции). При использовании этих критериев делаются предположения относительно поведения остатков 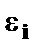– остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.

Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распре деления случайной составляющей 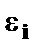. они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок 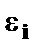(случайных остатков) тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.

Коэффициенты регрессии, найденные исходя из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является желательным свойством, так как только в этом случае они могут иметь практическую значимость. Несмещенность оценкиозначает, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оцениваний, остатки не будут накапливаться и найденный параметр регрессии bi можно рассматривать как среднее значение из возможного большого количества несмещенных оценок. если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.

Для практических целей важна не только несмещенность, но и эффективность оценок. Оценки считаются эффективными,если они характеризуются наименьшейдисперсией. Поэтому несмещенность оценки должна дополняться минимальной дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.

Степень реалистичности доверительных интервалов параметров регрессии обеспечивается, если оценки будут не только несмещенными и эффективными, но и состоятельными.Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии bi имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.

Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии ε. Условия, необходимые для получения несмещенных, состоятельных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

Исследования остатков 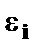. Предполагают проверку наличия следующих пяти предпосылок МНК:

v Случайный характер остатков;

v Нулевая средняя величина остатков, не зависящая от ;

v Гомоскедастичность – дисперсия каждого отклонения 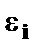. Одинакова для всех значений x;

v Отсутствие автокорреляции остатков. Значения остатков 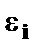. Распределены независимо друг от друга;

v Остатки подчиняются нормальному распределению.

В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и по методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков 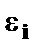. Не соответствует некоторым предпосылкам МНК, то следует корректировать модель.