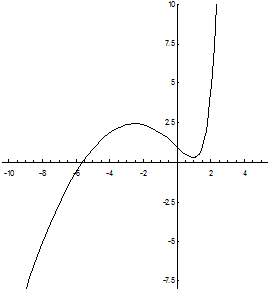Геометрическая интерпретация решений дифференциальных

уравнений первого порядка.

у a

b

A S

x

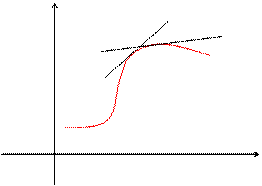
Как уже говорилось выше (см. Интегральные кривые. ), линия S, которая задается функцией, являющейся каким- либо решением дифференциального уравнения, называется интегральной кривой уравнения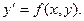

Производная y’ является угловым коэффициентом касательной к интегральной кривой.

В любой точке А(х, у) интегральной кривой этот угловой коэффициент касательной может быть найден еще до решения дифференциального уравнения.

Т.к. касательная указывает направление интегральной кривой еще до ее непосредственного построения, то при условии непрерывности функции f(x, y) и непрерывного перемещения точки А можно наглядно изобразить поле направлений кривых, которые получаются в результате интегрирования дифференциального уравнения, т.е. представляют собой его общее решение.

Определение. Множество касательных в каждой точке рассматриваемой области называется полем направлений.

С учетом сказанного выше можно привести следующее геометрическое истолкование дифференциального уравнения:

1) Задать дифференциальное уравнение первого порядка – это значит задать поле направлений.

2) Решить или проинтегрировать дифференциальное уравнение – это значит найти всевозможные кривые, у которых направление касательных в каждой точке совпадает с полем направлений.

Определение. Линии равного наклона в поле направлений называются изоклинами.

Численные методы решения дифференциальных уравнений.

Известные методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции, однако эти методы применимы для очень ограниченного класса уравнений. Большинство уравнений, встречающихся при решении практических задач нельзя проинтегрировать с помощью этих методов.

В таких случаях используются численные методы решения, которые представляют решение дифференциального уравнения не в виде аналитической функции, а в виде таблиц значений искомой функции в зависимости от значения переменной.

Существует несколько методов численного интегрирования дифференциальных уравнений, которые отличаются друг от друга по сложности вычислений и точности результата.

Рассмотрим некоторые из них.

Метод Эйлера.

(Леонард Эйлер (1707 – 1783) швейцарский математик )

Известно, что уравнение 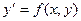задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке.

Если взять последовательность точек х₀, х₁, х₂, …. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию.

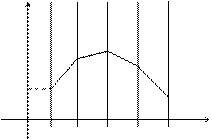y

M₂

M₁ M₃

M₀

y₀ M₄

0 x₀ x₁ x₂ x₃ x₄ x

При подстановке заданных начальных условий (х₀, у₀) в дифференциальное уравнение 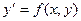получаем угловой коэффициент касательной к интегральной кривой в начальной точке

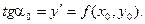
Заменив на отрезке [x₀, x₁] интегральную кривую на касательную к ней, получаем значение

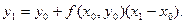
Производя аналогичную операцию для отрезка [x₁, x₂], получаем:

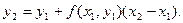
Продолжая подобные действия далее, получаем ломаную кривую, которая называется ломаной Эйлера.

Можно записать общую формулу вычислений:

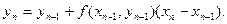
Если последовательность точек х_i выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу:

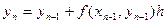
Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета.

Суть метода состоит в том, что в формуле 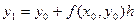вместо значения

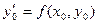берется среднее арифметическое значений f(x₀, y₀) и f(x₁, y₁). Тогда уточненное значение:

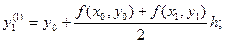
Затем находится значение производной в точке 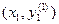. Заменяя f(x₀, y₀) средним арифметическим значений f(x₀, y₀) и 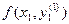, находят второе уточненное значение у₁.

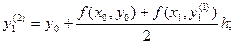
Затем третье:

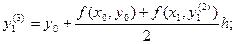
и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М₁ ломаной Эйлера.

Аналогичная операция производится для остальных значений у.

Подобное уточнение позволяет существенно повысить точность результата.

Метод Рунге – Кутта.

Метод Рунге – Кутта является более точным по сравнению с методом Эйлера.

Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора. (См. Формула Тейлора. )

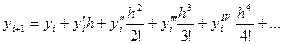
Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге – Кутта учитывает четыре первых члена разложения.

.

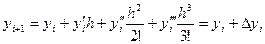В методе Рунге – Кутта приращения Dy_i предлагается вычислять по формуле:

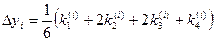
где коэффициенты k_i вычисляются по формулам:

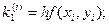
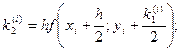
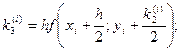
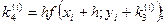
Пример. Решить методом Рунге – Кутта дифференциальное уравнение 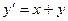при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.

Для i = 0 вычислим коэффициенты k_i.

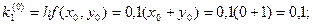
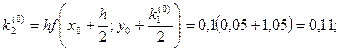
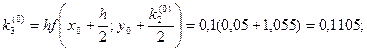
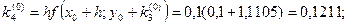
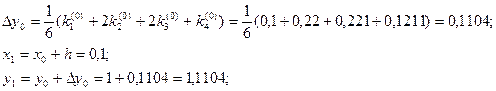
Последующие вычисления приводить не будем, а результаты представим в виде таблицы.

i	xi	k	Dyi	yi
			0,1000	0,1104
	0,1100
	0,1105
	0,1155
	0,1		0,1210	0,1325	1,1104
	0,1321
	0,1326
	0,1443
	0,2		0,1443	0,1569	1,2429
	0,1565
	0,1571
	0,1700
	0.3		0,1700	0,1840	1,3998
	0,1835
	0,1842
	0,1984
	0,4		0,1984	0,2138	1,5838
	0,2133
	0,2140
	0,2298
	0,5		1,7976

Решим этот же пример методом Эйлера.

Применяем формулу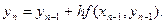

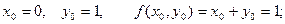
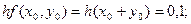
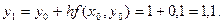
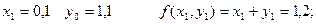
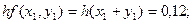
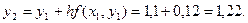
Производя аналогичные вычисления далее, получаем таблицу значений:

i
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi		1,1	1,22	1,362	1,528	1,721

Применим теперь уточненный метод Эйлера.

i
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi		1,1	1,243	1,400	1,585	1,799

Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции у на заданном отрезке.

Уравнение 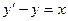является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.

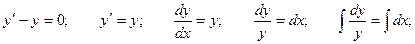
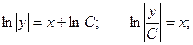
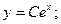
Решение неоднородного уравнения имеет вид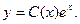

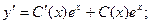
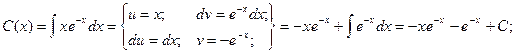
Общее решение: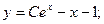

C учетом начального условия: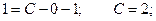

Частное решение: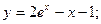

Для сравнения полученных результатов составим таблицу.

i	xi	yi
Метод Эйлера	Уточненный метод Эйлера	Метод Рунге - Кутта	Точное значение
	0,1	1,1	1,1	1,1104	1,1103
	0,2	1,22	1,243	1,2429	1,2428
	0,3	1,362	1,4	1,3998	1,3997
	0,4	1,528	1,585	1,5838	1,5837
	0,5	1,721	1,799	1,7976	1,7975

Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001. Кроме того, следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений. Это обусловлено тем, что во – первых полученное приближенное значение округляется на каждом шаге, а во – вторых – тем, что в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение. Таким образом происходит накопление ошибки.

Это хорошо видно из таблицы. С каждым новым шагом приближенное значение все более отличается от точного.

Дифференциальные уравнения высших порядков.

Определение. Дифференциальным уравнением порядка n называется уравнение вида:

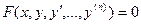
В некоторых случаях это уравнение можно разрешить относительно y⁽ⁿ⁾:

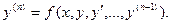
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.

Определение. Решение 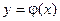удовлетворяет начальным условиям 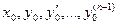, если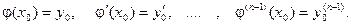

Определение. Нахождение решения уравнения 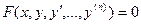, удовлетворяющего начальным условиям 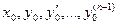, называется решением задачи Коши.

Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

Если функция (n-1) –й переменных вида 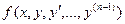в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по 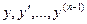, то какова бы не была точка ( 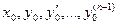) в этой области, существует единственное решение 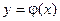уравнения 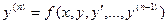, определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

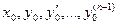Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.

Рассмотрим подробнее методы нахождения решений этих уравнений.

Уравнения, допускающие понижение порядка.

Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.

Уравнения вида y⁽ⁿ⁾ = f(x).

Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

…………………………………………………………….

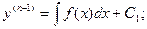
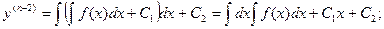
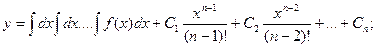
Пример. Решить уравнение 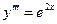с начальными условиями x₀ = 0; y₀ = 1;

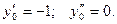
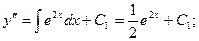
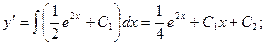
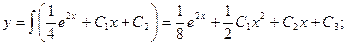
Подставим начальные условия:

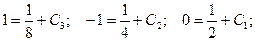
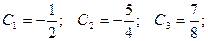
Получаем частное решение (решение задачи Коши): .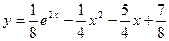

Ниже показана интегральная кривая данного дифференциального уравнения.