Математическое описание систем управления

Форма Коши - матричная форма записи системы ДУ решенных исключительно относительно первой производной координат САУ:

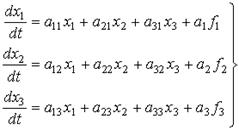
• x₁, x₂, x₃ - собственные координаты системы - ошибка системы x(t), воздействие на объект u(t), выходная координата - y(t), ...;
• a₁₁, ... , a₃₃ - постоянные коэффициенты (если система не является зависимой от параметра) - суммы и произведения постоянных времени Tj, коэффициентов усиления Kn;
• f₁, f₂, f₃ - воздействия на систему - сигнал задания g(t), помехи fj(t).

О форме Коши:

• Применяется в теории управления не часто.
• Удобна, если для расчетов использовать классические математические пакеты: MathCAD, MATLAB, Mathematica, Maple, Derive.
• Используется при построении аналоговых вычислительных моделей матричного типа (например, моделей на операционных усилителях).
• Уравнения могут быть решены относительно любой из фазовых координат xi.

Пространство состояний (ABCD-форма) - матричная форма записи системы ДУ САУ адаптированная для теории управления путем выделения из формы Коши алгебраических уравнений связывающих внутренние координаты САУ с выходной(ыми). Применяется для описания САР большого порядка, как правило, с несколькими входами / выходами и с перекрестными связями.

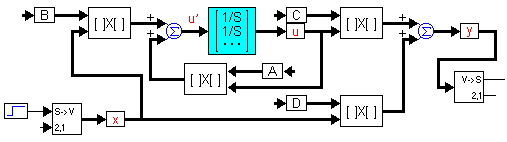
Изображенная на рисунке блок-схема позволяет решить систему ДУ представленную в форме "Пространства состояний":

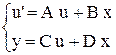
• xm _{x 1} - вектор входных переменных;
• yk _{x 1} - вектор выходных переменных;
• un _{x 1} - вектор переменных состояния (фазовых координат системы);
• An _x n - матрица коэффициентов системы;
• Bn _x m - матрица входных коэффициентов (матрица управления);
• Ck _x n - матрица выходных коэффициентов;
• Dk _x m - матрица коэффициентов пропорциональных каналов (матрица компенсации);
• n - порядок системы; m - кол-во входов; k - кол-во выходов (m<n).

О форме "Пространство состояний":

• Это вторая по частоте применений форма записи ДУ в ТАУ.
• Признана стандартом для программ математического моделирования VisSim, Simulink, и т.д., однако в большинстве случаев реализована в SISO-форме (с одним входом и одним выходом). Моделирующие программы для выполнения анализа (символьного или частотного) сводят любую модель пользователя к пространству состояний, заполняя в ходе первых шагов симуляции коэффициенты ABCD-матриц.
• Как правило, используется для построения моделей тех больших не поддающихся модуляризации, но не сложных систем, описание которых оптимально в матричной форме (таких мало). Для записи уравнений используются такие методы как: "Метод контурных токов", "Метод узловых потенциалов", - а так же их эквиваленты для других энергетических доменов (гидравлического, теплового, механического, ...).
• Матричное описание строго формализовано, и не требует понимания физической природы системы. Так же структура модели в "пространстве состояний" не позволяет разобраться во внутренней природе системы. Если эта форма записи ДУ применена обосновано, то модель, скорее всего, будет истинной.

ДУ решенное относительно регулируемой величины y(t) - уравнение движения

Система ДУ может быть преобразована к одному уравнению путем исключения промежуточных координат (обычно выходную координату выражают через координату задания):

.

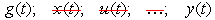Результатом подобного преобразования является уравнение движения системы:

D(p) y(t) = R(p) g(t) - N(p) f(t) , (4)

где:

• D(p) = a₀pⁿ + a₁p^n-1 + ... + an_-1p + an - характеристический полином;
• R(p) = D(p) - Q(p) = b₀p^m + b₁p^m-1 + ... + bm_-1p + bm - коэффициенты этого полинома определяют влияние задающего воздействия g(t) на регулируемую координату у(t), причем его степень меньше степени характеристического полинома, т.е. m<n;
• N(p) = d₀p^k + d₁p^k-1 + ... + dk_-1p + dk - коэффициенты полинома определяют влияние помехи f(t) на систему.

ДУ решенное относительно ошибки x(t) - уравнение ошибки

Если система ДУ (1) решается относительно ошибки системы, то получается уравнение ошибки замкнутой системы:

D(p) x(t) = Q(p) g(t) + N(p) f(t) (5)

где:

• D(p) = a₀pⁿ + a₁p^n-1 + ... + an_-1p + an - характеристический полином;
• Q(p) = D(p) - R(p) = c₀pⁿ + c₁p^n-1 + ... + cn_-1p + cn - коэффициенты полинома определяют влияние задающего воздействия g(t) на ошибку x(t);
• N(p) = d₀p^k + d₁p^k-1 + ... + dk_-1p + dk - коэффициенты полинома определяют влияние помехи f(t) на систему.

Передаточная функция - функция, связывающая один входной и один выходной сигналы САУ. Является формой записи системы ДУ САУ решённой относительно требуемой выходной координаты. Обычно ПФ записывается не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.

ПФ-ии получают из ДУ решенного относительно требуемой координаты системы. Для чего правую часть уравнения делят на характеристический полином D(p). Отношения полиномов в правой части при возмущающих воздействиях и есть ПФ-ии.

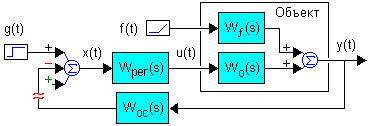
Для типовой структурной схемы замкнутой САУ различают 3 основные ПФ, применяемые для исследований:

1. W(p) = y(p)/x(p) * W_ос(p) = W_рег(p) W_о(p) W_ос(p) - ПФ разомкнутой системы;

2. Ф(p) = y(p)/g(p) - ПФ замкнутой системы;

3. Фx(p) = x(p)/g(p) - ПФ замкнутой системы по ошибке.

8. Усилительные устройства систем управления, как динамическое звено, требования, характеристики

Тиристорный преобразователь, как элемент САУ, представляет собой импульсную систему (СИФУ и выпрямитель ВП), преобразующую входной управляющий сигнал (напряжение 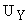) в функцию моментов отпирания тиристоров, изменяющую напряжение на входе двигателя 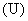, и описываемую дифференциальным уравнением: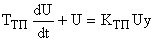

где 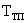– постоянная времени тиристорного преобразователя ( 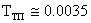сек для мостовой полностью управляемой схемы);

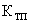– передаточный коэффициент тиристорного преобразователя .

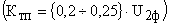При изменении напряжения управления на некоторую величину 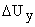изменяется напряжение на входе двигателя 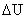. Тогда уравнение примет вид:

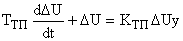
Переходя к операторной форме записи, получаем:

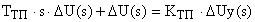
Отсюда выражение для передаточной функции тиристорного преобразователя принимает вид:

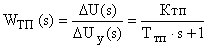
Широтно-импульсный преобразователь (ШИП) представляет набор электронных ключей, обеспечивающих импульсное изменение напряжения на нагрузке, подключенной к выходу этого преобразователя. В современной технике частоты коммутации ШИП лежат в пределах (2—50) кГц. Поэтому запаздывание в такой системе принимается равным нулю. Во многих приложениях ШИП представляется как безинерционный элемент с передаточной функцией 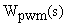вида:

,

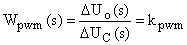где 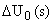, 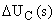– величины приращений изображений выходного и входного сигнала ШИП соответственно.

Более точное представление процессов в САУ, содержащей ШИП, может быть получено с использованием дискретного преобразования Лапласа.

9. Измерительные устройства систем управления как динамическое звено, требования, характеристики

Датчик тока (измерительный трансформатор тока) с фильтром, как элемент САУ, описывается дифференциальным уравнением вида: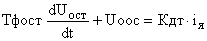

где 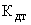– передаточный коэффициент датчика тока;

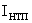– номинальный ток тиристорного преобразователя;

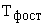– постоянная времени фильтра в обратной связи по току.

При изменении тока двигателя 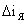изменяется напряжение на выходе 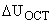, тогда уравнение в приращениях примет вид:

.

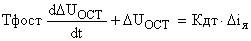Это уравнение в операторной форме записи представляется как:

.

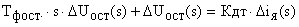Тогда передаточная функция датчика тока с фильтром примет вид:

.

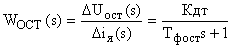Для практических расчетов можно пренебречь постоянной времени фильтра ( 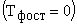, тогда передаточная функция датчика тока примет вид безинерционного звена: .

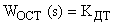Наиболее широко применяемым в системах управления технологическим оборудованием датчиком скорости является тахогенератор, на выходе которого включается дополнительный фильтр. Эти элементы САУ, описываются следующим дифференциальным уравнением: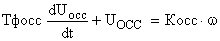

где 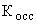– коэффициент обратной связи по скорости;

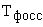– постоянная времени фильтра в обратной связи по скорости.

Тахогенератор является безинерционным звеном 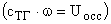, а инерционность вносится за счет фильтра ( 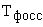). При изменении скорости тахогенератора на 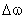изменится и напряжение на выходе — 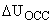. Тогда уравнение (3) в приращениях примет вид:

,

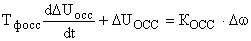Переходя к операторной форме записи, получаем:

,

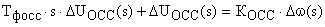Преобразовывая это уравнение, получаем передаточную функцию обратной связи по скорости:

.

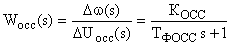В подавляющем большинстве станочного оборудования с числовым программным управлением используются измерительные преобразователи перемещения с импульсным или цифровым выходными сигналами. К ним относятся измерительные электромагнитные, электромашинные и фотоэлектрические преобразователи перемещения исполнительного механизма. В подавляющем своем большинстве точное математическое представление измерительных преобразователей перемещения требует использование дискретной математики. Однако для широкого класса систем автоматического управления возможно представление таких устройств как безинерционных элементов с передаточной функцией вида:

;

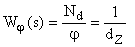где 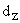– разрешающая способность измерительного преобразователя перемещения,

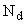– выходной сигнал измерительного преобразователя;

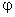— угол поворота вала измерительного преобразователя.

Разрешающая способность измерительных преобразователей, связанных с валом исполнительного механизма, определяется как

,

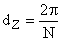где N – число меток измерительного преобразователя на один оборот его вала.

10. Исполнительные устройства систем управления как динамическое звено, требования, характеристики

В САУ используются различные исполнительные устройства, предназначенные для выполнения необходимых технологических операций. В качестве исполнительных преобразователей могут использоваться устройства, такие как электрические машины, гидравлические и пневматические преобразователи, нагревательные и акустические приборы. В технологическом оборудовании, используемом в механообработке, наиболее часто используются электромеханические преобразователи, в качестве которых используются электрические машины. Наиболее часто применяются электродвигатели постоянного тока, асинхронные электродвигатели и синхронные электрические машины, работающие в режиме бесконтактного двигателя.

Двигатель постоянного тока, как элемент САУ, описывается дифференциальными уравнениями якорной цепи и механической части двигателя:

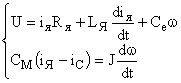
где 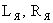– соответственно индуктивность и активное сопротивление якорной цепи;

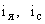— соответственно ток якорной цепи и ток нагрузки;

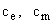– конструктивные постоянные двигателя;

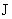– момент инерции двигателя.

При изменении напряжения на входе двигателя на некоторую величину 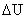изменяются ток двигателя 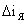и частота вращения двигателя 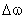и, пренебрегая обратной связью по противоЭДС двигателя 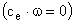, получаем уравнения якорной цепи и механической части двигателя в приращениях:

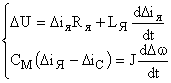
Преобразовывая уравнения и, считая 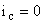, переходим к операторной форме записи данных уравнений:

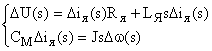
Из уравнений получаем выражения для передаточных функций якорной цепи и механической части двигателя:

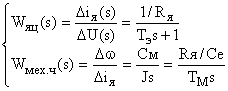
где 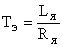– электромагнитная постоянная двигателя,

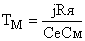— электромеханическая постоянная двигателя.

Согласно этой системе получаем, что развернутая структурная схема двигателя принимает вид, показанный на рис.1.

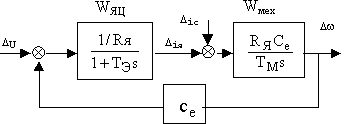
Рис. 1. Развернутая структурная схема двигателя

Свертывая развернутую схему, двигатель можно представить одним колебательным звеном (рис. 2):

,

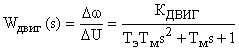где .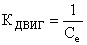

Рис. 2. Свернутая структурная схема двигателя

Асинхронный электродвигатель является наиболее широко используемой электрической машиной. Это объясняется простотой его конструкции и достаточно жесткими механическими характеристиками. Механическая характеристика имеет вид, представленный на рис. 3.

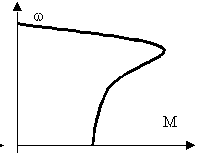
Рис. 3. Сравнительные механические характеристики электродвигателей.

Конструктивно асинхронный двигатель состоит из ротора, на котором расположена короткозамкнутая обмотка типа "беличья клетка", и статора. На статоре расположены обмотки управления, число которых определяется числом фаз питающего напряжения. Синхронная частота вращения вала двигателя определяется как

,

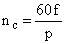где 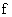– частота питающего напряжения

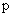– число пар полюсов статорной обмотки.

Для управления асинхронными двигателями используются частотные и амплитудные методы. В первом случае регулирование частоты вращения осуществляется путем изменения частоты питающего напряжения. Во втором случае для изменения частоты вращения вала асинхронного двигателя изменяется напряжение, подаваемое на статорные обмотки двигателя.

Точное математическое описание процессов, происходящих в асинхронном двигателе, представляется системой уравнений Парка-Горева. Оно используется при детальном рассмотрении систем автоматического управления с такими двигателями. Но так как, электромагнитные процессы, протекающие в асинхронных двигателях достаточно быстротечны, при их рассмотрении в большинстве приложений рассматривают только электромеханическую их составляющую. Поэтому передаточная функция асинхронного двигателя в большинстве приложений представляется как

,

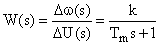где 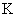– коэффициент пропорциональности между угловой скоростью вала и управляющим сигналом,

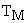– электромеханическая постоянная времени двигателя и исполнительного механизма.

В приводах подачи металлообрабатывающих станков широкое применение находят бесконтактные (бесколлекторные) двигатели (БКД). Такие электромеханические преобразователи состоят из синхронного двигателя, с ротором которого связан датчик положения ротора. Этот датчик обеспечивает коммутацию обмоток управления, расположенный на статоре электрической машины. На ее роторе располагаются постоянные магниты. Функциональная схема такого электромеханического преобразователя представлена на рис. 4.

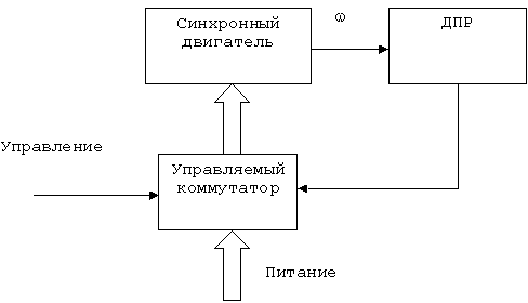
Рис. 4. Функциональная схема БКД.

Момент, развиваемый БКД определяется как:

,

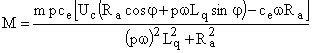где 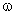— угловая скорость вала,

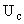– напряжение управления двигателем,

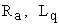– сопротивление и индуктивность фазной обмотки двигателя,

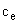– коэффициент пропорциональности между напряжением на фазных обмотках двигателя и угловой скоростью его вала,

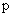– число пар полюсов двигателя,

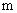– число фаз обмотки управления,

— угол сдвига между основной гармоникой ЭДС фазы и фазовым напряжением.

При малой индуктивности фазных обмоток двигателя и величине угла сдвига между основной гармоники ЭДС и фазовым напряжением, близким к 90 градусов, величина момента, развиваемого БКД, определяется как

.

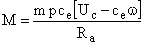Таким образом, вид механической характеристики БКД достаточно близок к аналогичным характеристикам двигателя постоянного тока. Поэтому, для исследования САУ, содержащих бесконтактные двигатели, используются передаточные функции, полученные для двигателей постоянного тока.

11. Счетно-решающие устройства систем управления, как элемент САУ, требования

В системах автоматики используют счетчики импульсов (1), логические элементы (2), микропроцессоры (3).

(1) – устройства для отсчета и запоминания количества поступивших электрических импульсов за некоторый промежуток времени. Для оценки частоты вращения (частотомеры).

(2) – для решения сложных задач оптимального поиска – реле времени электромеханического, пневматического и электронного типов.

(3) – для обработки цифровой информации – программно-управляемые устройства на основе больших микроэлектронных интегральных схем (БИС).

Кристалл – размер несколько мм 2 – в нем десятки тысяч полупроводниковых элементов; соединены между собой внутренними связями. Микропроцессоры – одно из наиболее перспективных направлений совершенствования управления работой строймашин на ближайшее будущее.

Микропроцессорная система моделирует реальный процесс функционирования машины и на основе прогноза ее состояния формирует набор машинных команд.