Основные соотношения между ВЧХ и переходной характеристикой

1. Начальное значение ВЧХ P(0) равно установившемуся значению переходной характеристики hу_ст = P( ) = P(0).

2. САУ с вогнутой ВЧХ (рис.97а кривая 1) не имеет перерегулирования, то есть ей соответствует монотонная переходная характеристика (рис.97б кривая 1).

3. САУ с трапециидальной ВЧХ (рис.97а кривая 2, такую ВЧХ можно аппроксимировать трапецией) имеет апериодическую переходную характеристику (рис.97б кривая 2), причем величина перерегулированияs_max не превышает 18%.

4. Кривые 3 и 4 на рис.97а соответствуют колебательной переходной характеристике (рис.97б кривая 3). Величина перерегулирования s_max тем больше, чем больше отношение P( )_max/P(0). Если это отношение стремится к бесконечности, то есть имеет место разрыв ВЧХ, то переходная характеристика приобретает вид незатухающих колебаний и САУ переходит на границу устойчивости. Величину перерегулирования можно приблизительно вычислить исходя из соотношения

s_max < .

Наличие отрицательного экстремума у ВЧХ (кривая 4) свидетельствует о повышенной колебательности системы.

5. Время переходного процесса t_пп можно оценить приблизительно по виду ВЧХ без построения кривой h(t). Оно определяется полосой частот w_п, при которыхP( ) > 0.2P(0) (рис.98). _п называют интервалом положительности P( ). При этом всегдаt_пп >p/ _п. Для кривой 1 рис.97а: t_пп 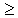4 / _п. Для кривой 2: t_пп 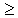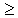(1..4)4 / _п. Для кривых 3 и 4 коэффициент пропорциональности больше, причем он тем больше, чем больше отношение P( )_max/P(0).

Метод трапеций

Этот метод основан на свойствах ВЧХ, следующих из полученной ранее формулы, которые мы рассмотрим без доказательств.

1. Свойство линейности: если ВЧХ можно представить суммой P( ) = SPi( ), то каждой составляющей Pi( )будет соответствовать составляющая переходной характеристики

,

при этомh(t) = (рис.99а). Поэтому, если ВЧХ имеет сложную форму, ее можно представить суммой трапециидальных ВЧХ, примыкающих к вертикальной оси. Затем все трапеции перерисовывают, перенося их основания на горизонтальную ось (рис.99б). Каждой такой трапеции соответствует своя составляющая переходной характеристики h_i(t), имеющая апериодический характер (рис.99в). Результирующая кривая строится суммированием данных составляющих.

2. Если умножить P( ) на постоянный множитель а, то соответствующая ейh(t)также умножается на а. То есть, чем выше ВЧХ, тем выше и переходная характеристика (рис.100).

3. Если аргумент w в выражении ВЧХ P( ) умножить на постоянный множительа, то аргумент в h(t)будет делиться на это число, то есть

То есть переходный процесс в случае P(a ) будет протекать в а раз быстрее, чем в случае P( ) (рис.101).

Рассмотрим трапециидальную ВЧХ (рис.102а). Она характеризуется коэффициентом наклона k = _{1 2}. Под единичной трапецией (рис.102б) понимают трапецию, две стороны которой совпадают с осями координат и равны по 1 в соответствующих масштабах; наклон kможет быть различным: P₁( ) = .

Подставляя это определение в выражение для определения h(t) можно вычислить кривую переходного процесса, соответствующую единичной трапециидальной ВЧХ. Эти расчеты были проделаны и составлены таблицы h_k-функций.

Для любой трапециидальной ВЧХ, на которые разбита реальная ВЧХ (рис.99б), можно построить подобную ей единичную трапецию со значением k = _{1 2}, где ₁ - частота, соответствующая перелому реальной трапеции, ₂ - основание трапеции реальной ВЧХ. Для данной единичной трапеции по таблице h_k-функций строят кривую h_k(k,t), где t- время. Затем, используя свойства 2 и 3 масштабирования ВЧХ и переходной характеристики строят кривую переходного процесса, соответствующего данной трапециидальной ВЧХ. Причем оба описанных процесса можно совместить: сначала задаются моментом времени t, для него по таблице находят значениеh_k(k,t), потом умножают это значение наP(0) (масштабирование по вертикальной оси) и откладывают полученное значение на графике h(t) для времени t = t/ ₂ (масштабирование по горизонтальной оси). Строя таким образом точки для различных моментов времени получают кривую

h_i(t/ ₂) = P(0) 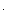h_k(k,t).

Данный алгоритм удобно оформить в таблицу:

t	hk(k,t)	t = t/ 2	hi(t) = P(0) hk(k,t)
.....	.....	.....	.....

После суммирования составляющих переходного процесса, соответствующих каждой трапеции, получают реальную характеристику h(t).

Описанный метод построения переходной характеристики называется методом трапеций.

Вопросы

1. Какую частотную характеристику используют для оценки качества управления САУ?
2. Какому значению на переходной характеристике соответствует точка ВЧХ при = 0?
3. Какую форму имеет кривая переходного процесса САУ с вогнутой ВЧХ?
4. Какую форму имеет кривая переходного процесса САУ с трапециидальной ВЧХ?
5. Какую форму имеет кривая переходного процесса САУ с ВЧХ, имеющей экстремум?
6. Как оценить время переходного процесса по виду ВЧХ?
7. В чем состоит метод трапеций?
8. Как используется в методе трапеций свойство линейности?
9. Как изменится кривая переходного процесса, если ВЧХ растянуть вдоль вертикальной оси?
10. Как изменится кривая переходного процесса, если ВЧХ растянуть вдоль горизонтальной оси?
11. Что называется единичной трапецией?
12. Сформулируйте алгоритм построения переходной характеристики в методе трапеций?

Синтез САУ

В ТАУ можно выделить две характерные задачи: 1) в заданной САУ найти и оценить переходные процессы - это задача анализа САУ; 2) по заданным переходным процессам и основным показателям разработать САУ - это задача синтеза САУ.

Вторая задача сложнее в виду своей неоднозначности, многое определяется творческими способностями проектировщика. Поэтому обычно задачу синтеза САУ ставится ограниченно. Считается, что основная часть системы уже задана, что обычно имеет место. Требуется синтезировать корректирующие звенья, то есть выбрать их схему и параметры. При этом необходимо, чтобы в результате коррекции САУ обеспечивался требуемый запас устойчивости; точность управления в установившихся режимах и качество управления в динамических режимах.