Пакет Control System Toolbox

Все объекты, используемые в пакете Control System Toolbox, объединены в один класс – lti-объекты. В зависимости от вида математического описания lti-объекты, могут быть заданы либо парой многочленов числитель/знаменатель передаточной функции (команда tf), либо нулями, полюсами и обобщенным коэффициентом передачи (команда zpk), либо четверкой матриц ( 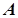, , 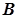, 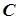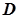), задающих модель системы в пространстве состояния (команда ss или dss). Команда dssтакже описывает линейную систему четверкой матриц ( 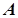, , 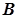, 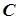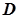), но используется тогда, когда уравнения переменных не разрешены относительно производных.

Указанные процедуры позволяют создать непрерывные и дискретные модели. Для дискретных моделей к числу входных параметров следует добавить значение параметра 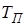- шага дискретизации, а вводимые значения коэффициентов должны задавать параметры дискретных передаточных функций (для команд tf и zpk) либо матриц конечно-разностных уравнений пространства состояния – при использовании команд ss и dss.

Известно, что z-передаточные функции могут быть представлены в двух видах. В теории управления используют переменную 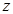и располагают многочлены числителя и знаменателя в порядке убывания степени этой переменной. Например 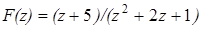. При цифровой обработке сигналов предпочитают записывать эту передаточную функцию как функцию переменной 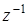. Например .

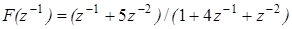При положительных степенях переменной 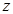используются команды tf и zpk с указанием параметра 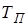, а при отрицательных степенях используется команда filt с указанием параметра 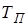, либо команды tf и zpk с указаним указателя переменной ‘variable’, ‘z^-1’.

Если значение 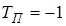, то период дискретности для дискретной системы не специфицирован, т.е. при выполнении команд tf, zpk, ss и filt периоду дискретности не присваивается никакого значения.

Ниже приведено несколько примеров, иллюстрирующих применение описанных команд.

% Создание LTI-моделей

H1=tf([1,4],[1,2,200] %Создание модели в форме tf

H2=tf([1,4],[1,2,200],0.1) %Создание дискретной модели

H3=tf([1,4],[1,2,200],-1) %с периодом дискретности 0,1.

%Время дискретности не определено.

H4=tf([1,4],[1,2,200],'variable','z^-1')

H5=filt([1,4],[1,2,200])

% Преобразование моделей

H1=tf([1,3,2],[1,7,12,0]) %Исходные данные.

F1=zpk(H1) %Переход от формы tf к zpk.

F2=ss(H1) %Переход от формы tf к ss.

F3=tf(F2) %Переход от формы ss к tf.

F4=tf(F1) %Переход от формы zpk к tf.

Результаты выполнения приведенных выше команд.

Transferfunction: %Передаточная функция H1

s + 4 %непрерывной системы

---------------

s^2 + 2 s + 200

Transfer function: %Передаточнаяфункция H2

z + 4 %дискретной системы с .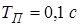

---------------

z^2 + 2 z + 200

Sampling time: 0.1

Transfer function: %Передаточнаяфункциядискретной

z + 4 %системы H3.Время дискретизации

--------------- %не определено (не специфицирована)

z^2 + 2 z + 200 %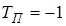

Sampling time: unspecified

Transfer function: %Передаточныефункции H4, H5

1 + 4 z^-1 %дискретных систем записаны

--------------------- %по убывающим степеням z

1 + 2 z^-1 + 200 z^-2

Sampling time: unspecified

Transfer function:

1 + 4 z^-1

---------------------

1 + 2 z^-1 + 200 z^-2

Sampling time: unspecified

Transfer function:

s^2 + 3 s + 2 %ПередаточнаяфункцияH1

------------------ %записана в формате tf

s^3 + 7 s^2 + 12 s

Zero/pole/gain: %Переходотформыtfкформеzpk

(s+2) (s+1)

-------------

s (s+4) (s+3)

a = %Переходотформыtfкформеss

X1x2 x3

x1 -7 -1.5 0 %Матрица коэффициентов a

X2 8 0 0

X3 0 2 0

b =

u1

x1 1%Матрица управления b

X2 0

X3 0

c =

x1x2 x3 %Матрица выхода c

Y1 1 0.375 0.125

d =

u1

Y1 0

Continuous-time model.

Transfer function: %Переходотформыssкформеtf

s^2 + 3 s + 2

------------------

s^3 + 7 s^2 + 12 s

Transferfunction: %Переходотформыzpkкформеtf

s^2 + 3 s + 2

------------------

s^3 + 7 s^2 + 12 s

Возможности пакета Control System Toolbox не ограничиваются приведенными командами. Для ознакомления с новыми командами и лучшего их использования целесообразно провести классификацию команд.

Функции пакета Control System Toolbox, описанные выше, могут быть классифицированы следующим образом.

Табл.1

Функции, создающие lti-модели.

set	Установка свойств
ss	Формирование ss-модели системы в явной форме Коши
dss	Формирование ss-модели системы в неявной форме Коши
tf	Формирование tf-модели в форме передаточной функции
zpk	Формирование zpk-модели
filt	Формирование модели в форме дискретного фильтра

Табл.2

Функции, преобразующие lti-модели.

c2d	Построение дискретной модели непрерывной системы
d2c	Построение непрерывной модели дискретной системы
d2d	Изменение периода дискретности
ss	Преобразование моделей к ss-форме
tf	Преобразование моделей к tf-форме
zpk	Преобразование моделей к zpk-форме

Табл.3

Функции, соединения lti-моделей.

parallel	Параллельное соединение (сложение lti-моделей)
series	Последовательное соединение (умножение lti-моделей)
feedback	Соединение с обратной связью
append	Объединение lti-моделей с добавлением входов и выходов
connect	Объединение lti-моделей с использованием матрицы соединений
star	Объединение взаимосвязанных многомерных моделей

Кроме приведенных выше функций к блоку команд формирования и преобразования lti-моделей следует отнести команды по извлечению информации об lti-моделях и команды, переопределяющие базисные функции. Однако при первом рассмотрении используются только команды, приведенные таб. 1, 2 и 3.

Для создания модели нужно предварительно либо привести уравнения всей системы к форме уравнений пространства состояний, либо найти передаточные функции системы. В общем случае это довольно сложная и громоздкая задача. В то же время реальные системы автоматического управления (САУ) состоят из соединенных между собой отдельных блоков (динамических звеньев), уравнения которых обычно достаточно просты. Поэтому в практике проектирования САУ принято использовать структурные методы, когда САУ задается как определенная схема соединения отдельных элементарных динамических звеньев, и фактически проектируется одно или несколько из этих звеньев таким образом, чтобы обеспечить заданное качество всей системы. В соответствии с этим в MatLab предусмотрена возможность "набирать" программно "схему" САУ путем предварительного ввода моделей звеньев, составляющих САУ, и последующего "соединения" этих звеньев в единую структуру. К процедурам, осуществляющим расчет характеристик соединений отдельных звеньев, относятся:

plus (minus) – выполняет "параллельное соединение" указанных при обращении звеньев, т.е. определяет характеристики модели системы из параллельно соединенных звеньев; особенностью является то, что вызов этих процедур может быть осуществлен не только обычным способом: путем указания имени процедуры и перечисления (в скобках после имени) идентификаторов соединенных звеньев, но и простым указанием идентификаторов звеньев, которые должны быть объединены, с простановкой между ними знаков "+" (при суммировании выходных сигналов звеньев) или "-" (при вычитании выходных сигналов).

parallel – осуществляет ту же процедуру параллельного соединения звеньев; в отличие от предыдущей процедуры может использоваться для многомерных систем и осуществления параллельного соединения лишь по некоторым входам и выходам;

mtimes (или знак "*" между именами звеньев) – осуществляет последовательное соединение звеньев, имена которых указаны; применяется для одномерных систем;

series – последовательное частичное соединение многомерных систем;

feedback – такое соединение двух звеньев, когда второе указанное звено составляет цепь отрицательной обратной связи для первого звена;

append – формальное объединение не связанных между собой систем (добавление выходов и входов второй системы к выходам и входам первой);

connect– установление соединений выходов и входов многомерной системы, созданной предварительно формальным объединением процедурой append; схема соединений задается матрицей 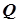соединений, указываемой как один из входных параметров процедуры;

inv – рассчитывает САУ, обратную указанной, т.е. такую, у которой выходы и входы поменяли местами;

vertcat – производит так называемую вертикальную конкатенацию (сцепление) систем (звеньев), т.е. такое их объединение, когда входы этих систем становятся общими, а выходы остаются независимыми; для такого объединения необходимо, чтобы число входов объединяемых систем было одинаковым; тогда число входов в результирующей системе останется таким же, как и в каждой из объединяемых систем, а число выходов будет равно сумме выходов объединяемых систем;

horzcat – осуществляет "горизонтальное сцепление" указанных систем, при котором выходы становятся общими, а входы добавляются.

Проиллюстрируем применение некоторых из этих процедур. Создадим модель управления двигателем постоянного тока состоящего из трех последовательно соединенных звеньев: регулятора 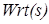; усилителя мощности 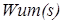; объекта регулирования 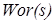. В цепи обратной связи стоит звено - 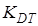, а регулятор тока состоит из параллельного соединения усилительного звена - 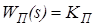и интегрирующего .

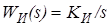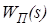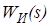Параллельное соединение и можно осуществить двумя способами: либо используя команду parallel.

Wn=tf(0.2,1) %Исходные данные

Transfer function:

0.2

Wi=tf(23.8,[1,0]) %Исходные данные

Transfer function:

23.8

----

s

Wrt=parallel(Wn,Wi) %Переменные команды parallel

Transfer function: %Результатвыполнения

0.2 s + 23.8 %командыparallel

------------

s

либо применяя операцию "Сложение" моделей

Wrt=Wn+Wi

Transferfunction: %Результат применения

0.2 s + 23.8 %операции «Сложение»

------------

s

Последовательное соединение звеньев 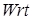, 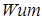и 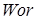можно так же осуществить двумя способами – применением процедур series.

Wum=tf(22,[0.003,1]) %Исходныеданные

Transfer function:

-----------

0.003 s + 1

Wor=tf(92,[0.008,1]) %Исходныеданные

Transfer function:

-----------

0.008 s + 1

Wps=series(Wrt,Wum*Wor)

Transfer function:

404.8 s + 4.817e004 %Результатвыполнения

---------------------------- %команды series

2.4e-005 s^3 + 0.011 s^2 + s

или

Wps=series(Wrt*Wum,Wor)

Transfer function:

404.8 s + 4.817e004 %Результатвыполнения

---------------------------- %команды series

2.4e-005 s^3 + 0.011 s^2 + s

либо просто перемножив передаточные функции моделей

Wps=Wrt*Wum*Wor

Transfer function:

404.8 s + 4.817e004

----------------------------

2.4e-005 s^3 + 0.011 s^2 + s

Теперь найдем модель замкнутой системы управления двигателем постоянного тока по управлению, используя команду feedback. В цепи обратной связи стоит усилительное звено .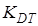

KDT=0.0345 %Коэффициент обратной связи

Wzu=feedback(Wps,KDT) %Передаточная функция замкнутой

%системы по управлению

Transferfunction:

404.8 s + 4.817e004

-------------------------

2.4e-005 s^3 + 0.011 s^2 + 14.97 s + 1662

Аналогично определяется передаточная функция замкнутой системы по возмущению.

UZB=feedback(Wor,KDT*Wrt*Wum)

Transferfunction: %Передаточная функция замкнутой

%системы по возмущению

0.276 s^2 + 92 s

-------------------------

2.4e-005 s^3 + 0.011 s^2 + 14.97 s + 1662

В приведенных примерах команды MatLab использовались для определения передаточных функций простых систем и их применение, во-первых, очевидно, а, во-вторых, не очень экономит время. Эффективность применения команд MatLab, которые приведены в урезанном виде, значительно возрастает при исследовании сложных многомерных систем с перекрестными связями.