Расчет пластин методом Бубнова-Галеркина.

Метод основан на свойстве ортогональности функций. Система функций φ_0, φ(_х), φ_к(х) – образует на интервале [а,в] ортогональную систему, если при k 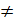l выполняется условие:

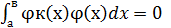(1)

Система функций 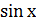, , 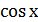, , 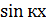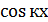ортогональна на отрезке [- 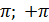], т.к. каждая пара этих функий удовлетворяет условию (1). Это свойство можно распространить на функцию нескольких переменных

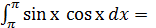0.5 sin²х 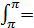0,5(0-0)=0

Если одна из этих функций равно 0, то ее можно считать ортогональной ко всем без исключения функциям, т.к. в этом случае условие (1)выполняется тождественно. В качестве такой функции в теоретического изгиба можно принять:

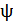(х,у)=D 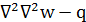(2)

Значит функция 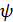(х,у) должна быть ортогональная к любой функции в заданной области.

Если прогиб задан в виде W(x,y) ∑_(k=1)^m ∑_(l=1)^n▒akl φkl (x,y), (*) то уравнение изгиба не удовлетворяет 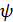(х,у) 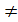0. Чтоб эта функция была ортогональна к аппроксимирующей функции φ_кl(х,у) в выражении (*)

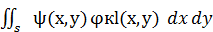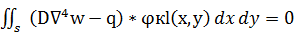= (3)

Интеграл выполняется по площади S срединной плоскости пластины.

Подставив (3) в (*) и выполнив интегрирование, получим систему линейных алгебраических уравнений относительно a_kl.

Уравнение (3) выражает в интегральной форме условие равенства нулю работы внешних сил и внутренних в пластинке на возможные перемещения φ_kl(x,y).

Расчет пластин методом Власова.

Рассмотрим вариационный метод В.З.Власова, который он сам назвал «практическим методом расчёта пластинок и призматических оболочек, имеющих несмещаемые рёбра». В соответствии с этим методом, прогиб w (x,y) в произвольной точке (х,у) пластинки представляется в виде произведения двух функций, каждая из которых зависит лишь от одной переменной: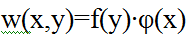

Одной из этих функций, например φ(х), следует задаваться, а другая является искомой. Для задания функции φ(х) В.З.Власовым предложен статический способ. Следуя ему, из пластинки выделяется бесконечно узкая полоска шириной dy, которая загружается вспомогательной нагрузкой, подобной заданной нагрузке, и в этой полоске-балочке определяется уравнение изогнутой оси. Такое уравнение, приведенное к безразмерному виду, по — Власову называют «функцией поперечного распределения прогиба» и обозначают φ(х).

А вторая функция, f (y), определяется решением обыкновенного дифференциального уравнения:

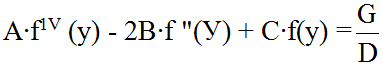
В этом уравнении обозначено:

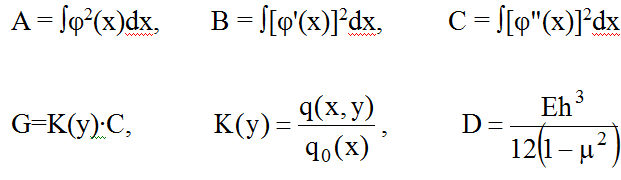
Расчет пластин методом конечных разностей.

Расчет пластин МКЭ.

1 этап. Составление КЭ схемы:

a) выбор типа КЭ ( по геометрии, виду апроксимации ……..)

б) Разбивка области на КЭ с номерами узлов и элем.

В) Описание заданных узловых нагрузок

2 этап. Формирование матриц жёсткости и вектора узловых сил.

а) Составление элементов МЖ и ВН в локальной системе координат

б) Преобразование элементов МЖ и ВН из локальной в глобальную систему координат

3 этап. Учёт заданных статических и кинематических граничных условий.