Поиск суммы степенных рядов с помощью почленного интегрирования и дифференцирования.

До сих пор мы искали область сходимости, то есть ГДЕ сходится ряд. А теперь научимся находить суммы рядов, обозначаемые через 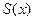. Проще всего, если ряд это геометрическая прогрессия, можно воспользоваться формулой 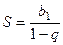. Однако далеко не всегда ряд это прогрессия. Тем не менее, бывают такие ряды, для котрых сумма производных или сумма первообразных от его слагаемых будет геометрической прогрессией. То есть, можно свести к прогрессии с помощью почленного дифференцирования или интегрирования.

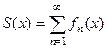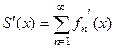тогда . Рассмотрим на примерах.

Пример.Найти сумму ряда .

Подробная запись: 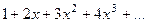заметим, что первообразные уже просто степенных функции, т.е. здесь легче найти не 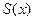а её первообразную.

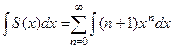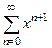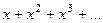= = а это уже геометрическая прогрессия со знаменателем 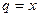. Её сумма 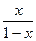, и это напомним, первообразная от 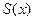. Тогда 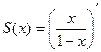= = 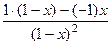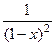. Ответ .

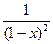А бывают примеры, где наоборот, сначала надо дифференцировать.

Пример. Найти сумму ряда .

Здесь тоже не прогрессия, но тот случай, когда можно свести к прогрессии. Если 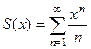то 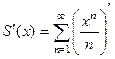= = 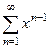= 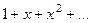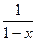. При этом, сходимость прогрессии обеспечена только при 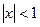, то есть .

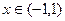А теперь, чтобы вернуться к 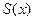, надо проинтегрировать. 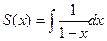= 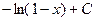, знак модуля под логарифмом не нужен, так как при 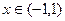будет 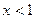, т.е. 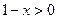, выражение и так положительное. Однако мы искале через первообразную, и там ещё есть неопределённая константа С. Чтобы её найти, надо присвоить какое-то значение 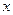одновременно в ряде и функции, например 0. 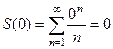а с другой стороны, это равно 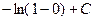, то есть 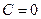. Ответ .

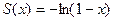На практике рассмотрим другие примеры, где есть особенности, связанные с реализацией этих методов. Например, иногда надо решать в 2 шага, а иногда домножать на что-либо, чтобы потом можно было продифференцровать и получить прогрессию.

ЛЕКЦИЯ № 12. 02. 05. 2017

Ряды Тейлора и Лорана.

В конце прошлой лекции мы изучали степенные ряды и находили суммы S(x). А бывает наоборот, обратная задача: дана функция, надо представить её в виде степенного ряда, т.е. «разложить в степенной ряд».

Ряд 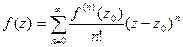- разложение функции 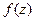в степенной ряд в окрестности точки , он называется рядом Тейлора этой функции. Соответственно, для действительных функций,

.

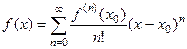Метод определения круга сходимости (до ближайшей точки разрыва).

Пусть . Если надо разложить её в ряд вида 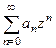, то центр 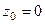, а ближайшая точка, где ряд точно расходится, это точка разрыва 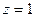. Тогда круг сходимости как раз и будет .

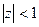Пример.Разложить в степенной ряд (ряд Тейлора). Первый способ - найти производные до любого порядка n, и подставить их в формулу.

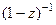= . Тогда:

= = .

=

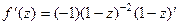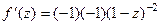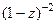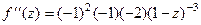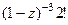
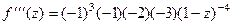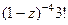= , и.т.д.

В точке 0 n-я производная равна n!

Тогда = = .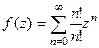

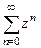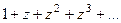Но не обязательно так искать все производные и устанавливать закономерность при их вычислении. Иногда количество слагаемых при дифференцировании экспоненциально возрастает (если там было произведение) на каждом шаге в 2 раза и равно 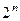, а закономерности очень сложно находятся. Так что напрямую по формуле считать не всегда удобно.

Второй способ - получать всё разложение сразу, используя геометрическую прогрессию. Применяем формулу суммы прогрессии 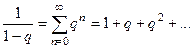при этом желательно заранее вынести все множители из числителя за пределы дроби, чтобы «очистить» числитель до 1, этим самым мы обеспечиваем то, что можно пользоваться упрощённой формулой суммы прогрессии 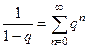, где .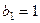

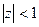Итак, . Заметим, что при эта функция может рассматриваться как сумма прогрессии (т.е. уже свёрутая по формуле суммы). Здесь знаменатель прогрессии 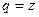. Тогда 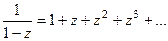как видим, то же самое и получили.

Рассмотрим разные модификации для других случаев.

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: по степеням 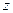, то есть в круге с центром 0.

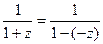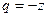Сумма вместо разности вовсе не является препятствием к тому, чтобы использовать прогрессию, запишем тогда и

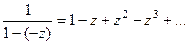если в знаменателе сумма, получается знакочередующийся ряд.

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: по степеням .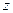

Решение. = = = = =

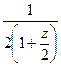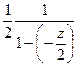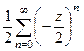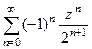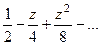
Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии по степеням , то есть в круге с центром в точке 1.

Здесь мы сначала определим круг сходимости. От точки 1 до точки разрыва 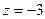расстояние 4, так что разложение в ряд возможно в круге .

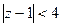Отделим разность искусственным путём, т.е. прибавим и отнимем 1.

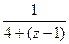= . А теперь далее не раскрываем блок вплоть до ответа, то есть эта скобка так и будет как единое целое.

= = = =

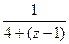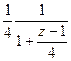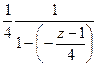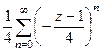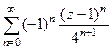. Заметим, что при этом знаменатель прогрессии 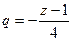, он должен быть меньше 1 по модулю, но так и есть, ведь круг сходимости 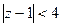, как уже заметили раньше.

Замечание.Если центр был бы в точке 2, то пришлось бы преобразовывать так: = = 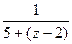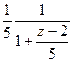. При этом получили бы условие 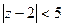что как раз и означает, что при сдвиге центра вправо, радиус круга увеличится, ведь он всё равно должен быть до ближайшей точки разрыва 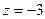. Эти ситуации отражены на чертеже:

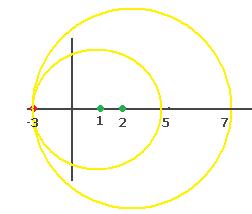
Приложения рядов Тейлора.

Приближённые вычисления.

Значения функции в точке можно приближённо вычислять с помощью разложения в ряд Тейлора, более того, во всех калькуляторах и компьютерах именно так и запрограммировано. Каждая функция там задана просто в виде набора коэффициентов ряда, и при обращении к функции именно это и вычисляется автоматически, с той точностью, с которой позволяет разрядная сетка калькулятора.

Так, вычислим 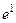. Ихвестно, что 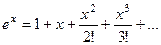. Тогда

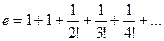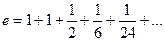= Так, для первых шагов сразу получаем значение 2,5 затем прибавляется 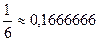и стало 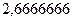а затем 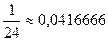станет 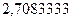и так с каждым шагом всё ближе к .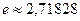