Области в комплексной плоскости и неравенства, задающие их.

Пример. 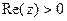правая полуплоскость.

Пример. 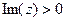верхняя полуплоскость.

Пример. 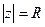- окружность радиуса R вокруг начала координат.

Пример. 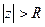- круг радиуса R вокруг начала координат.

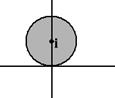
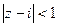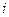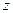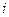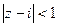
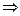
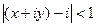
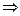
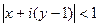
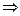
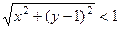
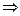
Пример. это круг радиуса 1 вокруг точки . Это неравенство задаёт следующее условние: удаление числа от фиксированного числа не превышает 1. Можно непосредственно преобразовать в уравнение круга в плоскости: 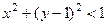а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке . Чертёж:

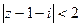
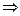
Пример. 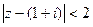это круг радиуса 2 с центром в точке 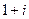, то есть точке (1,1) в плоскости.

Пример. Множество 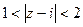это кольцо вокруг точки .

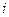ГЛАВА 3. РЯДЫ.

Числовые ряды.

Пусть дана последовательность 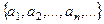. Бесконечная сумма: 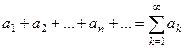называется рядом.

Если суммировать до какого-то номера n, то получается «частичная сумма» 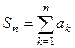. Часть, которая следует после слагаемого с номером n при этом называется остатком ряда. .

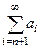Если сумма ряда обозначена 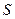, то: = .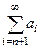

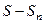Для каждого ряда существует последовательность частичных сумм:

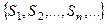ведь мы можем произвести конечное суммирование от 1-го до 1-го, затем от 1-го до 2-го, от 1-го до 3-го и так далее, и так для каждого n.

Определение 1.Если сходится последовательность частичных сумм ряда, то и соответствующий ряд называется сходящимся.

Лемма. Сходимость ряда эквивалентна сходимости любого из его остатков.

Доказательство. 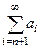= 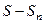. Частичная сумма содержит конечное количество слагаемых, она точно является конечным числом. Обозначим остаток через 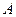. Тогда 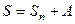. Если 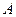конечно, то сумма двух конечных чисел 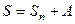тоже конечна. А если сумма ряда, то есть 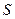, есть конечное число, то 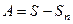разность двух конечных чисел, а значит тже конечное число. Таким образом, имеет место и необходимость, и достаточность.

Более подробное определение сходимости с помощью :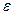

Определение 2. Ряд 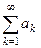называется сходящимся, если для всякого 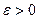существует такой номер 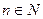, что .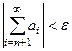

Определения 1 и 2 эквивалентны: если, начиная с некоторого номера, сумма оставшихся элементов меньше любой заранее заданной погрешности, это и означает, что частичные суммы стабилизируются при 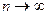, то есть существует предел .

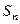Пример. Рассмотрим убывающую геометрическую прогрессию - кстати, прогрессия это один из важных частных случаев ряда.

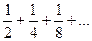Геометрическая интерпретация: возьмём квадрат

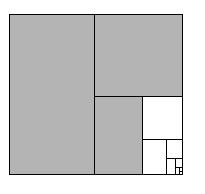
Если закрасить половину, затем четверть квадрата, и каждый раз половину того, что осталось до целого, то мы никогда не превысим площадь квадрата, а закрашенная площадь будет приближаться к 1.

Известна формула суммы бесконечной убывающей геометрической прогрессии: 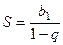. В данном случае .

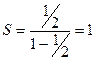Для погрешности 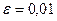найдём такой элемент, что частичная сумма отклоняется от суммы прогрессии менее чем на 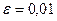, то есть остаток меньше .

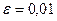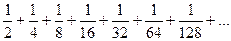После 4-го элемента,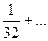

то есть для остатка, который тоже есть геометрическая прогрессия,

.

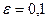
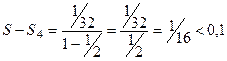Таким образом, после 4-го элемента, частичные суммы отклоняются от суммы менее чем на .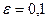

Теорема 1.Необходимый признак сходимости.

Если ряд 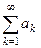сходится, то .

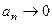Доказательство.Так как остаток ряда стремится к нулю, то есть сумма 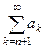= 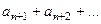по модулю меньше чем 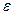, то одно первое слагаемое из остатка - тем более, меньше чем 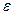. Получается, что при росте номера 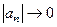, а значит и общий член ряда уменьшается к нулю, .

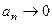Замечание. Это необходимый, а не достаточный признак! Т.е. если 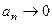, это ещё не всегда означает, что ряд сходящийся, а вот если общий член ряда не стремится к нулю, то ряд расходится, то есть такие ряды даже не надо исследовать, про них сразу же известно, что сходимости нет. Сейчас мы увидим пример, где слагаемые стремятся к 0, а сходимости всё же нет.

Гармонический ряд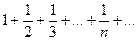

Доказательство его расходимости. Возьмём сумму от элемента номер n+1 до 2n. Докажем, что она больше 1/2, то есть для произвольного 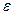, невозможно сделать её меньше, чем .

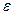Если была бы сходимость, то для любого 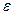остаток, начиная с какого-то номера, меньше чем 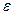. Запишем для n даже не весь остаток ряда, а его часть, а именно, последующие n элементов.

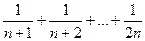
Наименьший элемент здесь 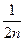. Если мы заменим все слагаемые на него, то сумма лишь уменьшится, т.е.

> = .

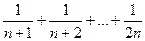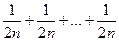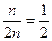Итак, часть частичной суммы от номера n+1 до 2n больше, чем 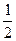, то есть не может быть меньше 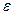. Определение сходимости не выполнено, ряд расходится. Здесь слагаемые уменьшаются к 0, но слишком медленно, недостаточно для сходимости.

Замечание.Тема «ряды» связана с темой «несобственные интегралы», там тоже рассматриваются только функции, стремящиеся к 0, и для них может быть либо сходимость, либо расходимость несобственного интеграла 1-го рода. Но там непрерывные, а здесь дискретные величины. Вспомним, что там тоже интеграл от 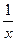был расходящимся, аналогичное мы сейчас увидели для ряда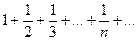

Суммы рядов в некоторых случаях можно найти, используя формулу Тейлора. Вспомним, например, 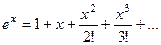если здесь положим 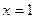, то получается 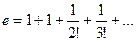, то есть сумма .

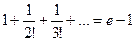Вспомним разложение функции 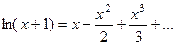, тогда при 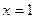получается .

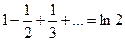Если все слагаемые здесь были бы со знаком «+» то это был бы гармонический ряд, расходимость которого доказали ранее.

Получается, что если знаки чередуются, то сходимость может быть из-за частичной компенсации слагаемых, а если взять по модулю, то сходимости может и не быть. В связи с этим возникают такие понятия: