Учебное пособие (курс лекций) 2 семестр

Приходовский М.А.

Математика

Учебное пособие (курс лекций) 2 семестр

Для специальности 09.03.03

Прикладная информатика в экономике

Томск

ТУСУР

Электронное пособие составлено и скорректировано с учётом реального проведения лекций на ФСУ в гр. 446-1-2 весной 2017 года.

Оглавление по темам

ГЛАВА 1. ИНТЕГРАЛЫ. 5

§1. Определения и основные методы. 5

§2. Интегрирование рациональных дробей. 11

§3. Интегрирование иррациональностей и тригонометрических выражений. 17

§4. Определённый интеграл и его приложения. 27

§5. Несобственный интеграл. 38

§6. Кратные интегралы. 46

ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. 60

§ 1. Дифференциальные уравнения 1-го порядка. 60

§ 2. Дифференциальные уравнения порядка n. 70

§ 3. Линейные дифференциальные уравнения порядка n. 74

§ 4. Системы дифференциальных уравнений. 87

§ 5. Комплексные числа, их связь с дифф.уравнениями. 90

ГЛАВА 3. РЯДЫ. 104

§ 1. Числовые ряды. 104

§ 2. Функциональные ряды. 117

§ 3. Степенные ряды. 120

§ 4. Ряды Тейлора и Лорана. 126

§ 5. Ряды Фурье.

Оглавление по номерам лекций

Лекция 1. 14.02.2017 5 - 15

Лекция 2. 21.02.2017 16 - 26

Лекция 3. 28.02.2017 27 - 38

Лекция 4. 07.03.2017 38 - 49

Лекция 5. 14.03.2017 50 - 59

Лекция 6. 21.03.2017 60 - 69

Лекция 7. 28.03.2017 70 - 79

Лекция 8. 04.04.2017 79 - 89

Лекция 9. 11.04.2017 90 - 101

Лекция 10. 18.04.2017 102 -114

Лекция 11. 25.04.2017 115 -125

Лекция 12. 02.05.2017 126 -134

Лекция 13. 16.05.2017

Лекция 14. 23.05.2017

Лекция 15. 30.05.2017

Приложение 1.Вопросы на доказательства. 135

Приложение 2. Мелкие и устные вопросы на знание теории

(для коллоквиумов). 140

Приложение 3. Задачи из лекций. 144

ЛЕКЦИЯ № 1. 14. 02. 2017

ГЛАВА 1. ИНТЕГРАЛЫ.

Определения и основные методы.

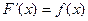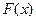Определение. Если , то называется первообразной от функции .

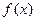Свойство.Если 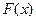первообразная, то 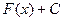(для любого 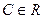) тоже является первообразной для той же самой функции .

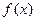Это легко доказать, действительно, = = .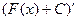

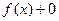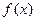Таким образом, первообразных бесконечно много, то есть, если поднять или опустить на любую высоту график 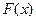, снова будет первообразная.

Свойство.Есл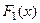и и 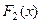две различные первообразные функции 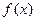, то .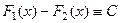

Доказывается так: 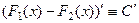, то есть .

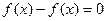Определение. Множество всех первообразных от одной и той же функции 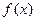называется неопределённым интегралом этой функции.

Обозначение: .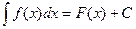

Свойства линейности.

1.

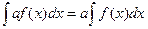
2.

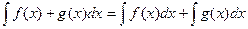
Замечание.

Для произведения свойство 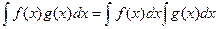не существует. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например 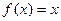, 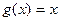. Тогда:

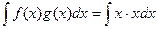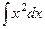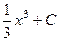= = , в то же время

= = .

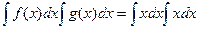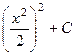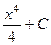Впрочем, можно даже рассмотреть произвольную, . Тогда ,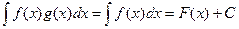

= .

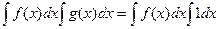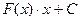Таблица основных интегралов.

( )

;

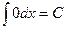
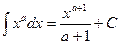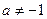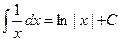
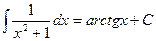
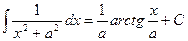
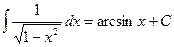
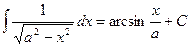
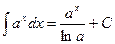
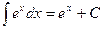
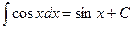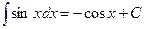
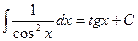
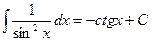
Объяснение причины возникновения модуля в 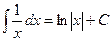. Функция 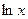существует только на правой полуоси, тогда как 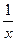имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция 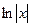является чётным продолжением 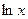на левую полуось, и именно она там является первообразной для 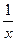при .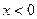

Методы интегрирования.

1. Преобразования подынтегральных выражений.

Различные преобразования, например, арифметические (домножить и поделить, прибавить и отнять), выделение полного квадрата, разбиение многочлена на множители, преобразования по тригонометрическим формулам, и т.д. нередко помогают упростить исходное выражение, разбить его на несколько более простых слагаемых, которые уже сводятся к интегралам табличного типа. На практике рассмотрены разнообразные примеры на виды этих преобразований. Часто нужно домножить и поделить, чтобы сформировать готовое выражение, являющееся производной от известной функции. Например,

Пример. = = .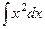

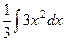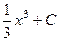Когда сформировали выражение 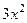, а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.

Аналогично, допустим, что мы помним, что 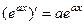. Тогда можно постараться сформировать готовое выражение типа 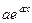внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:

Пример. = = .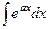

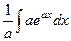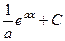Тригонометрические преобразования:

Пример. Вычислить .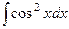

Решение. Применим формулу понижения степени.

= = =

= .

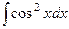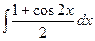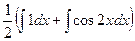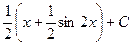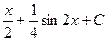Пример. Вычислить .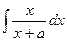

Решение. = = =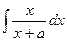

= .

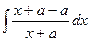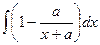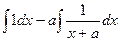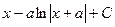Ответ. .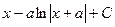

Замена переменной.

Бывают такие случаи, когда функция имеет вид 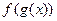, то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через 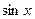или 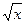. Делается замена на 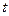, только нужно не забыть пересчитать 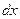, потому что 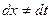, если только замена не является простым линейным сдвигом .

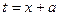Пример. Вычислить .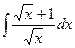

Решение. Сделаем замену 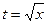, тогда , , .

= = = .

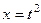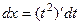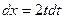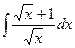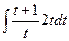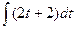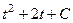Обратная замена: = = .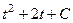

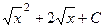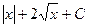Более того, область определения исходной функции 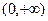из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: .

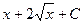Если в функции присутствуют корни разного порядка, например 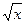и 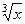, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от .

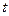Если 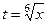, тогда: , .

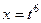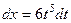Объяснение, почему все корни выразятся через целые степени :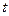

= ,

= .

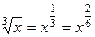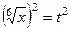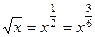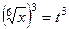Интегрирование по частям.

Существует более общий метод, чем подведение под знак дифференциала. Иногда вовсе не требуется, чтобы первообразная от того множителя, который подводится под dx, была как-то связана с остальной частью функции. Запишите формулу:

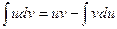
Такой короткий вид легче выучить наизусть, а теперь запишем более подробно, чтобы понять смысл.

.

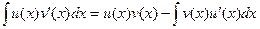Если есть два множителя, и один из них интегрируется довольно легко (он обозначен 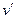) то можно перейти к интегралу, в котором наоборот, 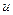понижено до производной, а 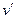повышено до первообразной. Иногда именно это помогает упростить дальнейшие вычисления.

Доказательство формулы.

Вспомним, что по правилу дифференцирования произведения, которое мы доказывали в прошлом семестре: 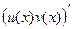= 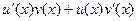. Тогда = .

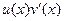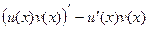Тогда и неопределённые интегралы от этих двух функций совпадают:

= .

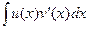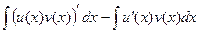Но первообразная от производной, это сама функция и есть, т.е.

.

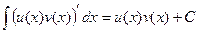Поэтому = .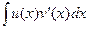

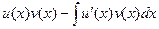Пример. Вычислить .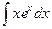

Решение. Если обозначить 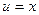, , 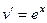то при переходе к 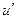степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было, 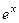. Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!

Составим таблицу:

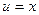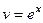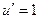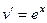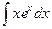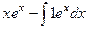= , тогда получаем ответ: .

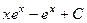Пример.Вычислить интеграл: 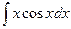Составим таблицу:

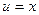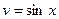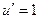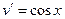После применения формулы, останется интеграл, в котором всего лишь один множитель, а не два, потому что 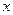переходит в 1, и один из множителей исчезает.

= = .

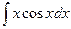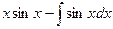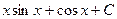А есть такие случаи, когда функция состоит не из 2 множителей, а всего из одного, но мы ведь всё равно можем считать, что второй множитель есть, только он равен 1.

Пример. .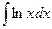

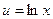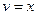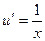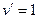Здесь производная от подынтегральной функции устроена лучше и проще, чем сама функция, но правда, пришлось допустить некоторое незначительное усложнение типа функции при переходе от 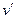к .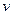

= = = .

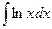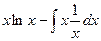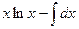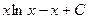ЛЕКЦИЯ № 2. 21. 02. 2017

Продолжение - рациональные дроби.

Ситуация 3. Если не все корни .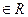

Возможно, что многочлен в знаменателе дроби не полностью разлагается на первые степени, так, могут присутствовать множители 2 степени типа 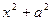или 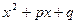с отрицательным дискриминантом, которые далее нельзя разложить, потому что у них нет действительных корней (есть комплексные корни, но они 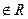). В этом случае вместо пары слагаемых в разложение надо включать одно, вида 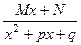, т.е. правильная дробь с максимально возможной степенью в числителе, должна содержать там линейную функцию. В некоторых примерах может потом оказаться, что 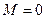, однако сразу искать в виде 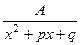нельзя, иначе может получаться противоречие при приведении к общему знаменателю.

А если неразложимые множители 2 степени сами кратные, то надо включить в сумму несколько слагаемых, где степени идут по нарастающей:

+ + ...

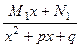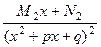Пример. Вычислить интеграл .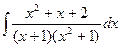

Решение. Ищем разложение в виде: = .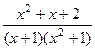

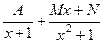Приводим к общему знаменателю.

=

=

=

= .

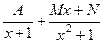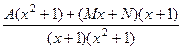
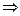
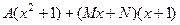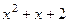
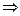
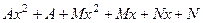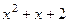
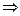
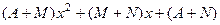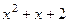Получаем систему:

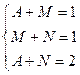. Из разности 1-го и 2-го уравнения, получаем .

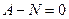В то же время, 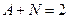. Тогда 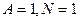. Тогда .

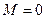Итак, заменим в интеграле «большую» дробь на сумму маленьких, каждая из которых приводится к табличному интегралу.

= = .

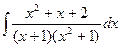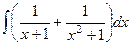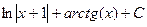Итак, в этом параграфе мы рассмотрели все типы рациональных дробей. Других случаев нет, т.к. неделимых множителей 3 степени уже быть не может, для многочлена 3 степени есть хотя бы один действительный корень.

Иррациональности.

Если в подынтегральной функции присутствует корень какого-то порядка 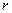, то есть 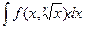, то замена 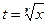позволяет полностью избавиться от корней в выражении и свести к рациональной дроби.

Из 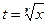следует 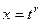, , 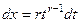то есть как видим, пересчёт дифференциала при замене тоже не добавляет ничего, кроме константы и целой степени от .

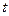Рассмотрим сразу более общий случай: если функция содержит несколько корней разного порядка, т.е. .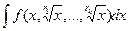

Тогда нужна замена на корень порядка r = НОК (r₁,...,r_k).

r это наименьшее общее кратное всех порядков, которые там есть.

Именно тогда все корни перейдут в целые степени от 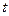. Так, к примеру, если 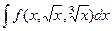, то НОК = 6. Замена: 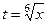, тогда: 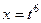, 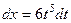. Каждый корень становится целой степенью от :

= ,

= .

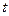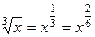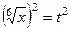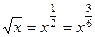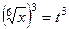В общем случае степень равна 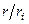, то есть, какого множителя не хватает до наименьшего общего кратного, такая степень от и получится.

Рассмотрим на примере, содержащем 3 разных корня.

Пример Вычислить интеграл .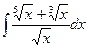

НОК (2,3,5) = 30. Поэтому замена .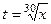

Тогда 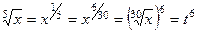. Дополняющий множитель до НОК для числа 5 как раз и есть 6, ведь НОК = 30.

Другие корни пересчитываются аналогично:

,

.

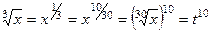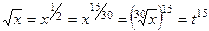Надо ещё также пересчитать дифференциал для новой переменной .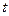

.

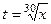
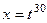
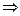
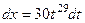Теперь подставим всё это в интеграл.

= = =

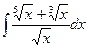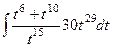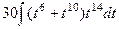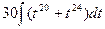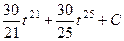= = , и после обратной замены:

.

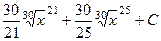Если 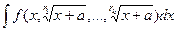т.е. под корнем некоторое линейное выражение, то решается практически так же, замена 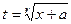, где r это тоже наименьшее общее кратное. Более сложная ситуация, когда под корнем разные линейные функции.

Например, 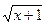и 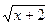. Если один корень заменить на t , 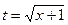, то 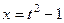, тогда 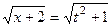. Такие будут рассмотрены чуть позже в этом параграфе, они решаются с помощью тригонометрических функций.

Если интеграл вида 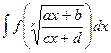(где r - целое число), то замена 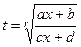сводят всё к рациональной дроби от t.

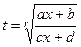
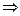
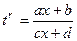
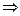
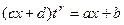
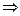
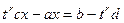
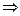
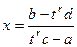то есть 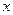выражено в виде рациональной дроби от 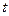, содержащей только целые степени.

Дифференциал тоже выразится в виде рациональной дроби:

= =

.

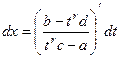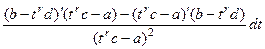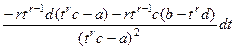ЛЕКЦИЯ № 3. 28. 02. 2017

Определённый интеграл.

Определение. Пусть функция 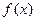определена и непрерывна на 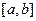. Введём разбиение отрезка 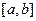на n частей: 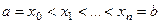. Каждый из n элементарных отрезков 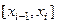обозначим 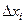, а его длину 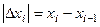. Возьмём какую-то произвольную точку на каждом из этих отрезков, 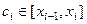. Следующая сумма: 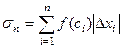называется интегральной суммой. Предел 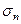при 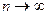и при условии, что 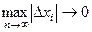(то есть разбиение отрезка измельчается повсюду, а не только в какой-то его части) называется интегралом функции 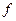по отрезку .

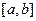Обозначение: .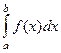

Геометрически 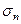означает сумму площадей прямоугольников, высота каждого из которых равна значению в выбираемой точке :

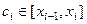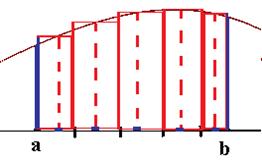
Чем больше n, тем более узкие прямоугольники получаются, и в пределе эта величина стремится к величине площади между графиком и осью. Геометрический смысл интеграла: площадь криволинейной трапеции под графиком (если график выше оси). Впрочем, интеграл может быть и меньше нуля, так, если 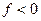то это площадь, расположенная между графиком и осью 0х, взятая с отрицательным знаком.

ЛЕКЦИЯ № 4. 07.03.2017

Несобственный интеграл.

Если криволинейная трапеция бесконечно вытянута вправо или вверх, то может быть конечная площадь. Примеры:

Пример. 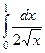= = 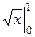1.

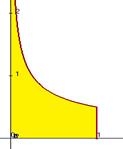
Но ведь область значений E(f) не является ограниченной. При вычислении мы даже и не заметили, что функция неограниченная в окрестности точки 0, т.е. 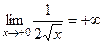. Так как первообразная ограниченная, и в неё можно просто подставить 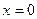и 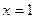. Вот график этой функции :

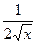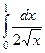можно рассматривать как предел .

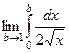Пример. Вычислить .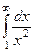

Решение. Такой интеграл можно рассматривать как предел интегралов вида 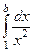при 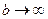. Если вычислить 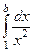то получится 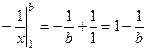. Предел .

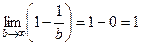Несмотря на неграниченность трапеции под интегралом, площадь конечна. Здесь область определения D(f) не является ограниченной. Тем не менее, трапеция слишком узкая, т.е. её ширина убывает достаточно быстро, чтобы площадь не превысила некоторое число. Так может быть, к примеру, если площади криволинейных трапеций между соседними целыми абсциссами убывают со скоростью сходящейся геометрической прогрессии.

Определение. Если функция 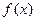определена и непрерывна на 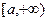, то предел 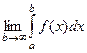называется несобственным интегралом 1-го рода от функции 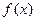, и обозначается .

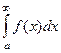Аналогично с помощью предела можно определить и несобственный интеграл 2 рода. Так, если функция имеет бесконечный предел на правой границе b то надо отступить на некоторое расстояние 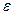и посчитать конечный интеграл, а затем перейти к пределу.

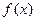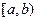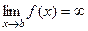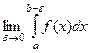Определение. Если функция определена и непрерывна на и при этом предел , то называется несобственным интегралом 2-го рода от функции 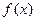, и обозначается .

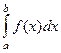Итак, если неограниченная D(f), то интеграл называется несобственным интегралом 1-го рода, а если E(f) то несобственным интегралом 2-го рода.

Если предел существует и является конечным числом, то несобственный интеграл называется сходящимся, если предел не существует или равен бесконечности, то интеграл называется расходящимся.

Кстати, для сравнения, геометрическая прогрессия также бывает сходящейся либо расходящейся. Если площадь такой бесконечно вытянутой криволинейной трапеции разбить на части по целым числам, например от 1 до 2, от 2 до 3 и так далее, то если они образуют сходящуюся прогрессию, и в сумме равны некоторой константе, то интеграл сходится.

Примеры расходящихся несобственных интегралов.

Пример. 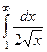= = 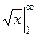. Здесь расходимость из-за неограниченности первообразной.

Пример. 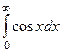= = 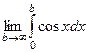= = 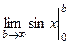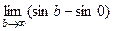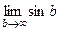. Но этот предел не существует, синус колеблется от -1 до 1 и при увеличении переменной его график не стремится ни к какой конкретной высоте. И хотя даже функция ограничена, несобственный интеграл расходится. Площадь криволинейной трапеции, при увеличении 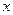, то растёт, то снова убывает.

Пример = = = = = .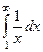

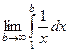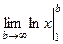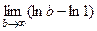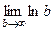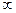Примеры сходящихся несобственных интегралов.

Пример. = = .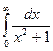

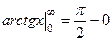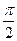Пример. = = .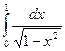

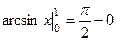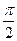Теорема 1. Несобственный интеграл 1-го рода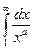

сходится тогда и только тогда, когда ,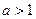

несобственный интеграл 2-го рода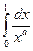

сходится тогда и только тогда, когда .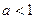

Доказательство. Сначала рассмотрим первообразную.

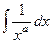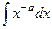= = , что можно записать в виде .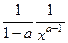

Если пределы интегрирования от 1 до 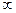, то не бесконечный результат получится лишь в том случае, когда переменная в знаменателе, то есть степень 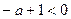, то есть 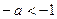, то есть .

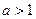А если пределы интегрирования от 0 до 1, то наоборот, наличие переменной в знаменателе приводит к тому, сто предел бесконечен, интеграл расходится. То есть для сходимости, надо чтобы степень была такая, чтобы переменная находилась именно в числителе. Тогда 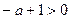, то есть, 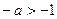, 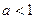. Что и требовалось доказать.

Обратите внимание, что в случае 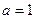расходятся оба этих интеграла, так как первообразная -это логарифм, а он не ограничен ни при 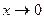, ни при .

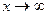Для таких интегралов 2 рода, для сходимости надо, чтобы степень перешла в положительные, например, если у функции степень 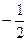, а у первообразной на 1 больше, уже 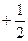. Если же она 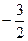, то после интегрирования станет 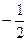, то есть ещё не переходит через 0 в положительные.

Примеры

1 рода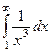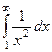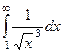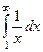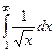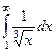
2 рода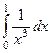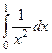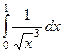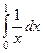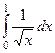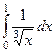
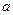			1,5		1/2	1/3

Жёлтым цветом здесь выделены сходящиеся интегралы.

Теорема 2. Несобственный интеграл сходится 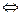первообразная на границах интегрирования имеет конечный предел.

Идея доказательства. Действительно, 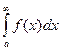= = 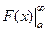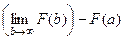. Второе слагаемое конечное число. Первое слагаемое (предел) есть конечное число тогда и только тогда, когда разность - конечное число. То есть, сходятся именно те несобственные интегралы, где график первообразной стабилизируется по высоте, т.е. имеет конечный предел 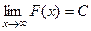. Если интеграл 1 рода, то 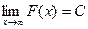равносильно сходимости.

Следствие (необходимый признак сходимости).

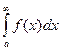сходится .

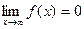Действительно, если 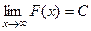то = = .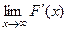

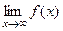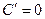Замечание. Это необходимый, а не достаточный признак, то есть, из сходимости следует, что f стремится к 0, но не наоборот. То есть, при 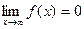могут быть как сходящиеся, так и расходящиеся интегралы, а вот если 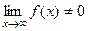, тогда только расходящиеся.

Рассмотрим 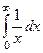и 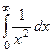. Здесь в обоих случаях 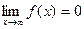выполнено. А тем не менее, первых из них расходится, а второй сходится. Их графики кажутся похожими, но ведь второй уменьшается существенно быстрее: так, при 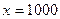значение у первой их них 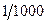, а у второй 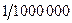, то есть в 1000 раз меньше! То есть кроме условия 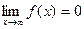важна ещё и скорость сходимости. Но если это условие не выполнено, то сходимости точно нет, в этом и состоит понятие «необходимый» признак.

Как мы увидели, овольно нередкой является ситуация, когда производная стремится к бесконечности, а сама функция (то есть её первообразная) в той же точке является конечной. Геометрическая интерпретация. Рассмотрим верхнюю полуокружность. При приближении к точке (1,0) касательная стремится к вертикальному положению, тангенс угла её на