Интервальный вариационный ряд
При большом объеме выборки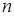 
работа с вариационными рядами представляет определенные неудобства, и тогда наблюдаемые данные группируют.
Группировка должна наиболее полно выявлять существенные свойства распределения. Существуют формулы для определения оптимального количества интервалов, но в психологии считается, что следует брать от 5 до 15 интервалов.
Первый способ построения интервального ряда.
Если у исследователя нет предварительной информации о характере распределения признака, то лучше задавать равные интервалы, при этом длина интервала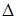 
определяется по формуле 
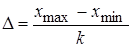, где 
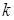- количество выбранных интервалов (число 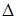округляется до целого значения).
Начало первого интервала равно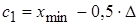 
, а конец 
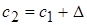(это будет одновременно и началом второго интервала). Условимся все интервалы считать с открытым правым концом: 
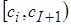. Построение интервалов заканчивается, если в интервал попало наибольшее значение признака 
.
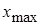Далее подсчитывают число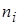 
значений признака, попавших в каждый интервал (с учетом открытого правого конца). Получается таблица, называемая интервальным вариационным рядом.
| Интервалы | 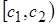 | 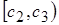 | … | 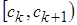 | Сумма |
| Частоты, |  |  | … |  | |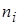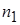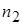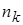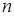
Относительные частоты,  |  |  |  |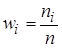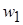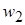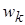
Второй способ построения интервального ряда.
Весь диапазон значений признака от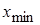 
до 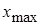разбивается на равные интервалы, называемые также классами. Затем все варианты совокупности распределяются по этим интервалам. Порядок действий:
§ Определяется число классов по формуле Стэрджеса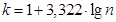 
.
§ Затем определяется размах выборки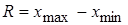 
.
§ Находим ширину интервала 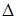по формуле 
.
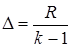§ Находим нижнюю границу первого интервала: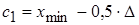 
.
§ Начальные и конечные значения всех последующих интервалов можно вычислить путем последовательного прибавления величины интервала к значениям конца предыдущего интервала: ,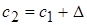 
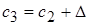и так далее.
Пример построения интервального вариационного ряда.
Пусть измерен некоторый показатель для 30 испытуемых:
23, 29, 35, 7, 11, 18, 23, 30, 36, 18, 11, 8, 13, 20, 25,
27, 14, 30, 20, 20, 24, 19, 21, 26, 22, 16, 26, 25, 33, 27.
Это статистический ряд.
Расставим экспериментальные данные в возрастающем порядке, то есть построим вариационный ряд:
7, 8, 11, 11, 13, 14, 16, 18, 18, 19, 20, 20, 20, 21, 22,
23, 23, 24, 25, 25, 26, 26, 27, 27, 29, 30, 30, 33, 35, 36.
Число классов (интервалов) для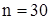 
:
.
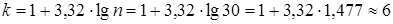Минимальное и максимальное значения: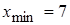 
, 
.
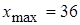Вариационный размах: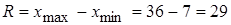 
.
Величина интервала: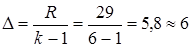 
.
Находим границы интервалов:
;
; 
;
; 
;
; 
.
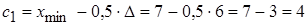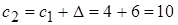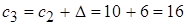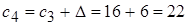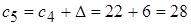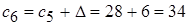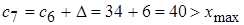Построим интервальный вариационный ряд.
| Номера интервалов | Интервалы | Серединные значения интервалов | Частоты |
| 4 – 10 | |||
| 10 – 16 | |||
| 16 – 22 | |||
| 22 – 28 | |||
| 28 – 34 | |||
| 34 – 40 |
Определение. Полигоном частотназывают ломаную, отрезки которой соединяют точки с координатами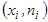 
; полигоном частостей – с координатами 
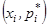, где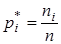 
, 
.
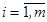Полигон служит для изображения дискретного статистического ряда.
Полигон частостей является аналогом многоугольника распределения дискретной случайной величины в теории вероятностей.
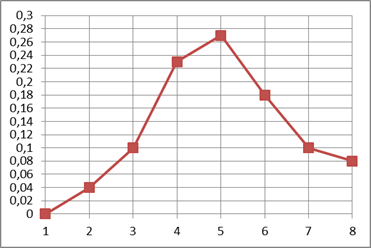
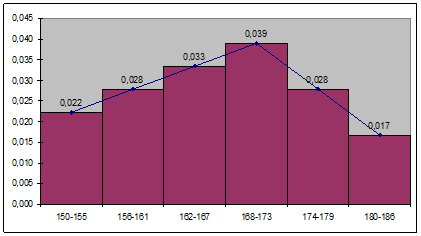
Определение. Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основания которых расположены на оси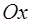 
и длины их равны длинам частичных интервалов 
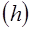, а высоты равны отношению:
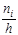- для гистограммы частот; 
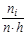- для гистограммы частостей.
Гистограмма является графическим изображением интервального ряда.
Площадь гистограммы частот равна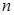 
, а гистограммы частостей равна 1.
Гистограмма позволяет сделать предварительное суждение о плотности распределении генеральной совокупности.
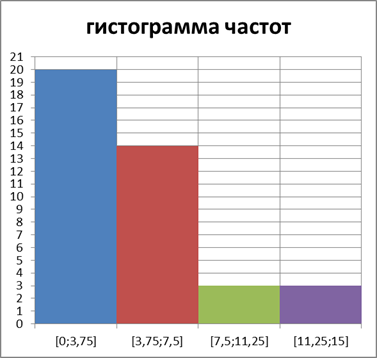
Можно построить полигон для интервального ряда, если его преобразовать в дискретный ряд. В этом случае интервалы заменяют их серединными значениями и ставят в соответствие интервальные частоты (частости). Полигон получим, соединив отрезками середины верхних оснований прямоугольников гистограммы.
