Апериодическое звено первого порядка

Звено имеет неколебательный (апериодический) характер переходного процесса и описывается дифференциальным уравнением первого порядка вида

где k – коэффициент передачи, характеризующий свойства в статическом режиме; Т – постоянная времени, характеризующая инерционность звена.

Примерами апериодических звеньев первого порядка могут быть: бак с водой, входной величиной которого является приток жидкости х_вх=Q₁, а выходной – уровень жидкости х_вых=Н (рис. 3.6,а); емкость для сглаживания давления воздуха, входной величиной которой является приток воздуха х_вх=Q₁, а выходной – изменение давления Р₂ в емкости х_вых=Р₂ (рис. 3.6,б); электрическая цепь, содержащая сопротивление R и конденсатор с электрической емкостью С, входной величиной которой является напряжение, приложенное к точкам 1 – 2, а выходной – напряжение, снимаемое с точек 3 – 4 (рис. 3.6,в).

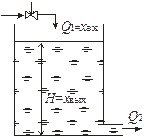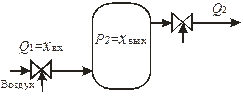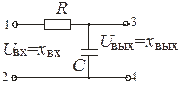а	б	в
Рис. 3.6. Примеры апериодических звеньев первого порядка

Инерционными звеньями первого порядка являются конструктивные элементы, которые могут накапливать и передавать энергию или вещество. В гидравлических элементах накопителем вещества является объем бака, в пневматических – емкость (объем) резервуара; в электрических – накопителем электрического тока служит емкость конденсатора.

11. Апериодическое звено второго порядка. Его математические модели, характеристики и свойства. Технические примеры.

Апериодическое звено 2-ого порядка

Описывается уравнениями

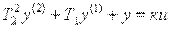или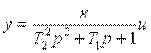

где T₁, T₂– постоянные времени (T₁> 2T₂). При этом корни характеристического уравнения 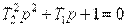являются вещественными и отрицательными. Знаменатель передаточной функции апериодического звена 2-ого порядка может быть разложен на множители

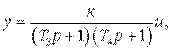
где ; .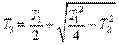

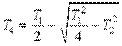В связи с этим, апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, соединенным последовательно между собой и имеющим коэффициент усиления k и постоянные времени T₃ и T₄.

Переходная функция апериодического звена второго порядка имеет вид

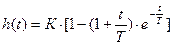
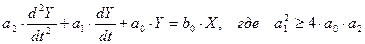Дифференциальное уравнение, описывающее динамику звена:

или (а₂р² +а₁р+а₀)*у=в_0*х

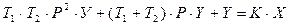
в канонической форме:

передаточная функция: W_В (p)=К/[(Т₁р+1)(Т₂р+1)];

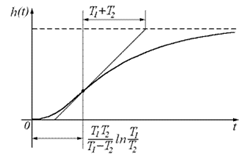
теоретическая кривая h(t):

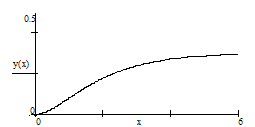
Апериодическое звено второго порядка так же, как и звено первого порядка, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты.

Инерционными звеньями второго порядка являются обычно такие конструктивные элементы автоматических систем, которые содержат два накопителя вещества или энергии: последовательное соединение двух гидравлических емкостей (рис. 3.8,а) или последовательное соединение двух цепей RС (рис. 3.8,б).

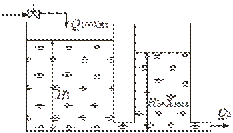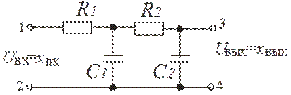а	б
Рис. 3.8. Примеры апериодических звеньев второго порядка

12. Колебательное звено второго порядка. Его математические модели, характеристики и свойства. Технические примеры.

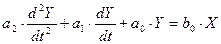а) Дифференциальное уравнение, описывающее динамику звена:

или (а₂р² +а₁р+а₀)*у=в_0*х

в канонической форме:

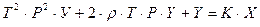б) аналитическое выражение переходной характеристики h(t):

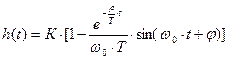в) передаточная функция: W_К (p)=К/(Т²р²+2rТр+1);

г) теоретическая кривая h(t):

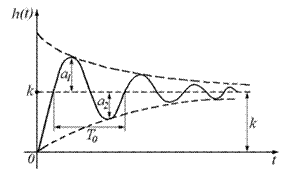
Амплитуды первых двух колебаний определяют величину - .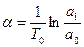

Чем ближе коэффициент затухания к единице, тем меньше амплитуда колебаний, чем меньше Т, тем быстрее устанавливаются переходные процессы.

Структурная схема колебательного звена будет выглядеть следующим образом:

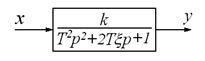
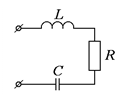Примером колебательного звена является любая RLC - цепь.

Свойства колебательного звена определяются тремя параметрами: постоянной времени Тк, относительным коэффициентом затухания и передаточным коэффициентом

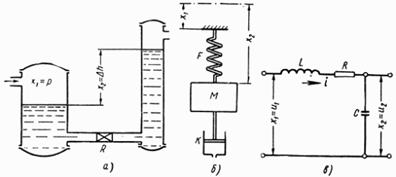
Примеры элементов систем автоматического регулирования, которые могут рассматриваться как устойчивое колебательное звено: а — сообщающиеся сосуды, соединенные через гидравлическое сопротивление — масса М, соединенная с пружиной F и снабженная катарактом К; в — электрическая цепь

13. Апериодическое звено (инерционное звено первого порядка).

Апериодическое это такое звено, которое описывается дифференциальным уравнением:

Tdy(t)/dt + y(t) = kx(t)

где: k – коэффициент усиления. Т – постоянная времени апериодического звена, сек.

Структурная схема выгляди следующим образом.

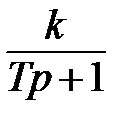х (t) y(t)

Рис.53. Представление апериодического звена на структурных схемах.

Передаточная функция апериодического звена равна:

W( p) = k/ (Tp + 1).

Переходная характеристика апериодического звена представлен на рисунке 54. Такой процесс называется монотонным, он близок к апериодическому.

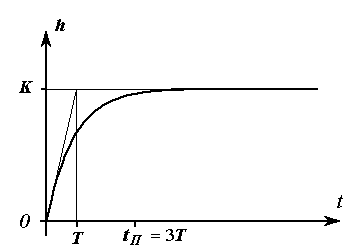
Рис. 54. Переходная функция апериодического звена

Коэффициент усиления звена определяет уровень, к которому стремится переходная характеристика с течением времени. Касательная, проведенная в начале координат к переходной характеристике, пересекает этот уровень в момент времени, равный постоянной времени апериодического звена Т.

Апериодическое звено не сразу, а постепенно реагирует на ступенчатое воздействие, в этом и проявляется его инерционность, которая численно может характеризоваться величиной постоянной времени, поскольку переходный процесс заканчивается примерно за 3Т. За время 3Т переходная характеристика достигает 95% уровня, к которому она стремиться при стремлении времени к бесконечности.

В качестве примера апериодического звена можно привести RC – цепочку, если за входное воздействие принять напряжение u. Здесь постоянная времени T = RC , а коэффициент k = 1 . Размерность постоянной времени [ RC ]=сек. Коэффициент усиления в силу одинаковой природы входного выходного сигналов безразмерен и равен в данном случае единицы. Другими примерами могут служить: термопара, электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.

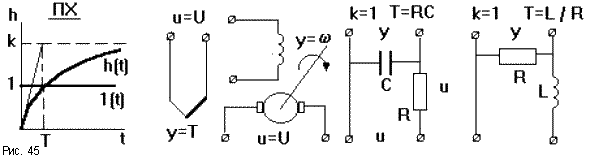
Рис. 55. Примеры апериодических звеньев.

14. Колебательное звено (Инерционное звено второго порядка).

Колебательное звено это такое звено, дифференциальное уравнение которого имеет вид: T2d2y(x)/dt2+ 2 δ Tdy(t)/dt + y(t) = kx(t)

Звено характеризуется тремя параметрами:

Т – постоянная времени, сек;

k – коэффициент усиления,

δ - декремент затухания, характеризующий скорость затухания свободных колебаний звена.

Если δ < 1, звено называется колебательным.

Если δ > 1, звено называется также и инерционным звеном II порядка.

Как видно из дифференциального уравнения, передаточная функцияколебательного звена имеет вид: W( p) = k/ (T12p2 + Т2р+1).

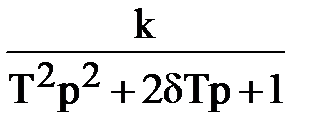х (t) y(t)

T=T1, T2=2 δ T

График переходной функции колебательного звена приведен на рисунке.

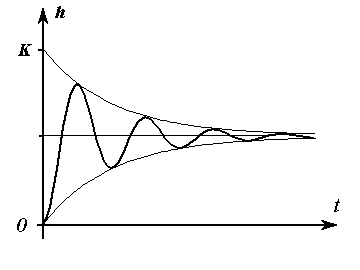Рис. 57. Переходная функция колебательного звена

С течением времени значения характеристик стремятся к величине коэффициентов усиления звеньев. При δ > 1 колебательность переходной функции исчезает, функция становится апериодической. Примерами колебательного звена могут служить пружина, имеющая успокоительное устройство, электрический колебательный контур. Зная характеристики реального устройства можно определить его параметры как колебательного звена. Передаточный коэффициент k равен установившемуся значению переходной функции.

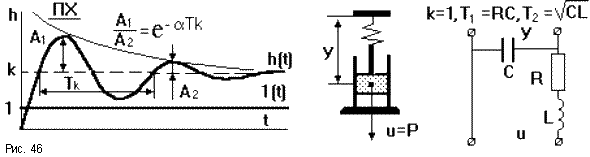
Рис. 58. Пример колебательного звена.

15-16