Решение матричных антагонистических игр

В качестве основного допущения в теории игр предполагается, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях партнера. Предположим, что имеется конечная антагонистическая игра с матрицей выигрышей первого игрока 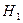и соответственно матрицей выигрышей второго игрока 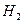. Пусть Игрок 1 считает, что какую бы стратегию он ни выбрал, Игрок 2 выберет стратегию, максимизирующую его выигрыш, и тем самым минимизирующую выигрыш Игрока 1.

Таким образом, Игрок 1 выбирает i-ю стратегию, которая является решением задачи

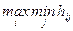
Игрок 2 точно также стремится обеспечить себе наивысшую величину выигрыша (или, что эквивалентно, наименьшую величину проигрыша) вне зависимости от выбранной стратегии противника. Его оптимальной стратегией будет столбец Н₀ с наименьшим максимальным платежом. Таким образом, Игрок 2 выберет j-ю стратегию, которая является решением задачи

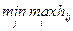
В итоге, если Игрок 1 придерживается избранной стратегией (называемой максиминнной стратегией), его выигрыш в любом случае будет меньше максиминного значения (называемого «нижней ценой игры»), т.е.

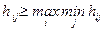
Соответственно, если Игрок 2 придерживается своей минимаксной стратегии, то его проигрыш будет не больше максиминного значения (называемого «верхней ценой игры»), т.е.

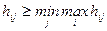
В случае, когда верхняя цена игры равна нижней, т.е. 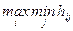= 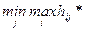, оба игрока получают свои гарантированные платежи, а значение h_ij* называется ценой игры.

Элемент матрицы h_ij матрицы выигрышей, соответствующей стратегиям, называется седловой точкой матрицы Н.

В случае, если цена антагонистической игры равна 0, игра называется справедливой.

Рассмотрим игру, в которой Игрок 1 располагает двумя стратегиями, а Игрок 2 – тремя. Матрица выигрышей Игрока 1 имеет вид:

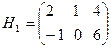
Замечание. Поскольку мы рассматриваем пример антагонистической игры, то матрица выигрышей Игрока 2 будет Н₂=-Н₁.

Игрок 1 рассчитывает, что если он выберет первую стратегию (т.е. первую строку матрицы Н₁), то противник выберет свою вторую стратегию (т.е. второй столбец) так, что выигрыш будет равен 1. Если же он выбирает вторую стратегию, то противник может выбрать первую стратегию, так что выигрыш будет равен -1.

Проанализировав полученные значения: Игрок 1 останавливается на своей первой стратегии, которая обеспечивает ему максимальный гарантированный выигрыш, равный 1.

Точно также Игрок 2 рассматривает свои наихудшие варианты, когда противник выбирает первую или вторую стратегии, или когда противник выбирает вторую стратегию, когда Игроком 2 выбран третий столбец. Этим варианты соответствуют максимальным значениям столбцов 2, 1 и 6.

Взяв минимальные значения этих максимумов, Игрок 2 останавливается на своей второй стратегии, при которой его проигрыш минимален и равен :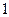

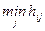
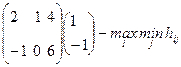
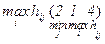
Следовательно, в этой игре существуют совместные выборы стратегий, те. Е

.

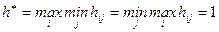Следовательно в этой игре разумно ожидать, что противники будут придерживаться избранных стратегий. Матричная антагонистическая игра, для которой 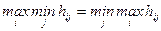- называется вполне определенной, или игрой имеющей решение в чистых стратегиях.

Однако не все матричные антагонистические игры являются вполне определенными.

Игры, в которых выполняется строгое неравенство, называется не полностью определенными играми (или играми, не имеющими решения в чистых стратегиях).

Рассмотрим пример такой игры:

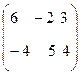
Для этой игры .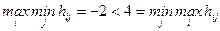

В итоге если игроки будут следовать предложенным выше правилам, то Игрок 1 выберет стратегию 1 и будет ожидать, что Игрок 2 выберет стратегию 2, при которой проигрыш равен -2, в то время как Игрок 2 изберет стратегию 3 и будет ожидать что Игрок 1 выберет стратегию 2 с выигрышем равным 4.

Однако если Игрок 2 выберет свою третью стратегию, то Игрок 1 поступит правильнее, выбирая вторую стратегию, а не первую стратегию. Аналогично, если Игрок 1 выберет первую стратегию, Игроку 2 выгоднее выбрать вторую стратегию, а не третью. По всей видимости, в играх подлобного типа принцип решения в чистых стратегиях оказывается непригодным.

В описанной ситуации игрокам становится важно, чтобы противник не угадал, какую стратегию он будет использовать. Для осуществления этого плана игрокам следует пользоваться так называемой смешанной стратегией.

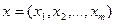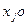По существу, смешанная стратегия игрока представляет собой схему случайного выбора чистой стратегии. Математически ее можно представить как вероятностное распределение на множестве чистых стратегий данного игрока. В итоге вектор , где соответствует вероятности применения Игроком 1 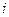-той стратегии и 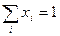, задает смешанную стратегию этого игрока. Аналогично определяется смешанная стратегия у Игрока 2 .

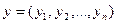Мы будем предполагать использование игроками их смешанных стратегий независимым, так что вероятность, с которой Игрок 1 выбирает 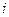тую стратегию, а Игрок 2 - 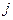- ю, равна 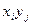. В этом случае платеж 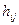. Суммируя по 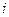и 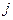, найдем математическое ожидание выигрыша Игрока 1:

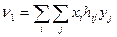
или матричных обозначениях

.

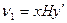На множестве смешанных стратегий Игрок 1, стремящийся достичь наибольшего из гарантированных выигрышей, выбирает вектор вероятностей 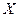так, чтобы получить максимум минимальных значений ожидаемых выигрышей, т.е. он решает задачу:

.

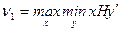Аналогично целью Игрока 2 является достижение минимума максимальных значений своих проигрышей, т.е. он решает задачу

.

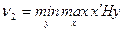Фундаментальным результатом теории игр является так называемая Теорема о минимаксе, которая утверждает, что сформулированные задачи Игрока 1 и Игрока 2 всегда имеют решение для любой матрицы выигрышей 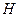, и кроме того, .

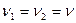Как и для вполне определенных игр, стратегия 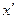Игрока 1 называется Максиминной стратегией, стратегия Игрока 2 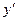- минимаксной стратегией, значение 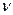- ценой игры; в случае, когда 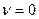игра называется справедливой.

Очевидным следствием из Теоремы о минимаксе является соотношение:

.

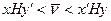которое означает, что никакая стратегия Игрока 1 не позволит выиграть ему сумму большую, чем цена игры, если Игрок 2 применит свою минимаксную стратегию, и никакая стратегия Игрока 2 не даст возможности проиграть ему суму меньшую, чем цена игры, если Игрок 1 применяет свою максиминную стратегию.

Это верно также и для чистых стратегий, как для частного случая смешанных стратегий. (Т.к. чистая стратегия – это стратегия, используемая с вероятностью 1): Использование любой чистой стратегии, в случае если противник использует свою оптимальную стратегию, не позволяет выиграть больше (проиграть меньше) цены игры.

Это факт часто используют для разработки конкретных алгоритмов решения антагонистических матричных игр.

Вычисление оптимальных стратегий значительно усложняется с ростом числа стратегий. Для поиска оптимальных стратегий можно использовать несколько подходов.

Для уменьшения размерности игры используется доминирование строк и столбцов. Обычно говорят, что 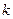-я стока матрицы 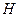доминирует 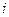-ю строку (т. е. одна чистая строка доминирует другую), если 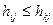для всех 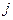, 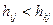хотя бы для одного .

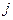Аналогично 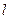-й столбец доминирует 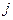-й столбец, если 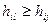для всех 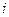, 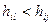хотя бы для одного .

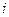Смысл этого определения состоит в том, что доминирующая стратегия никогда не хуже, а в некоторых случаях даже лучше, чем доминируемая стратегия. Отсюда, важный вывод – игроку нет необходимости использовать доминируемую стратегию. Это позволяет на практике все доминируемые строки и столбцы отбросить, что позволит уменьшить размеры матрицы (заметим, что этот подход может использоваться также при поиске решения в чистых стратегиях).

Пример. Рассмотрим игру со следующей матрицей:

→ третья строка этой матрицы доминирует вторую

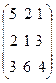
Исключение второй строки приводит к матрице: 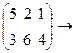третий столбец в этой урезанной матрице доминирует второй, и исключение второго столбца дает: .

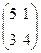В итоге, если можно найти решение для полученной игры, то его легко использовать для решения исходной игры, просто прописав исключенным строкам и столбцам нулевые вероятности.

Другой метод упрощения матрицы основан на свойстве, согласно которому аффинное преобразование матрицы платежей (т.е. преобразование всех элементов матрицы 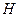по правилу 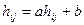, где 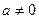) не изменяет решения игры; кроме того, цена преобразованной игры 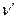может быть получена из цены первоначальной игры по такому же правилу: 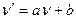. Это означает, что для задания игры в принципе безразлично, в каких единицах измеряются выигрыши (в рублях или долларах) прибавление (вычитание) некоторой фиксированной суммы 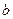изменит на такую же сумму выигрыш (проигрыш) каждого из игроков не меняя решение игры.

Это свойство может быть использовано для упрощения и придания наглядности матрице выигрышей (использовано по аналогии с операциями над матрицами – умножение матрицы на постоянное число, сложение и вычитание строк, кроме того, это свойство позволяет любую матричную антагонистическую игру сделать справедливой, для этого необходимо вычислить цену игры из всех элементов матрицы выигрышей).

Кроме того может быть использован графический способ для решения игры 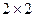(и вообще игр 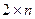или ).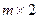

Например, матрица выигрышей имеет вид: .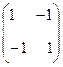

Пусть Игрок 1 выбирает свою первую стратегию с вероятностью 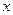, а вторую с вероятностью 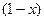. Если Игрок 2 выбирает свою первую стратегию, то (из первого столбца матрицы) математическое ожидание для Игрока 1 будет равно 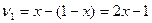. Если Игрок 2 выбирает свою вторую стратегию, то в соответствии со вторым столбцом матрицы: .

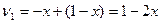Каждое из этих уравнений может быть изображено графически отрезком прямой линии в области 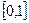на графике с координатам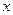и и .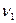

Они представлены в виде лини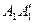й и 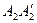, которые пересекаются в точке 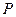. При данном 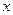Игрок 1 может получить две величины 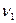, если Игрок 2 применяет свои чистые стратегии. Промежуточные значения 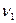соответствующие точкам между этими графиками, получаются если Игрок 2 применяет смешенные стратегии. Меньшая из этих величин, соответствующая каждому значению 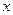показывает тот минимум, который может получить Игрок 1, выбирая стратегию .

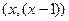Следовательно, линия 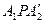показывает платеж, который Игрок 1 может гарантированно получить при любой стратегии Игрока 2. Игрок 1 выбирает такое значение 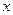, чтобы достичь наивысшей точки. Как показано на графике этой точкой является точка 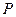, для которой .

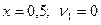Аналогично можно проанализировать игру Игрока 2, который использует свою первую стратегию с вероятностью 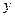, а вторую с вероятностью 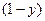. На графике рядом ломанная 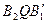представляет наибольший проигрыш Игрока 2, при различных выборах 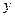. Игрок 2 выбирает 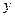так, чтобы достичь низшей точки на этой линии, т.е. точки 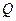, для которой 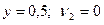. Следовательно, игроки должны применять свои стратегии с одинаковой вероятностью равной 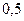и цена игры при этом будет 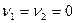, т.е. описанная игра справедлива.

Следующий метод решения матричных игр базируется на свойстве, приведенном выше, гарантирующем, что применение чистых стратегий Игроком 2 (Игроком 1) против оптимальной смешанной стратегии Игрока 1 не позволяет ему проиграть меньше (выиграть) больше чем значение цены игры .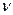

Это позволяет сформулировать следующую задачу для Игрока 1:

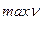
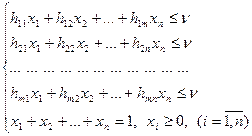
Приведенная задача типичная задача линейного программирования и решается его методами. Задача Игрока 2 выглядит аналогично и является двойственной задачей линейного программирования к задаче Игрока 1

Таким образом, в общем случае для решения матричной антагонистической игры размерностью 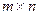необходимо решить пару двойнойственных задач линейного программирования, в результате чего найдется набор оптимальных стратеги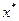й и 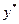и цены .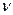