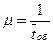Понятие марковского случайного процесса
Процесс работы СМО представляет собой случайный процесс.
Под случайным процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными характеристиками.
Процесс называется процессом с дискретными состояниями, если его возможные состояния s1, s2, s3,… можно заранее перечислить, а переход системы из одного состояния в другое происходит мгновенно (скачком).
Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние заранее не фиксированы, случайны.
Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Это означает, что состояние СМО меняется скачком в случайные моменты появления каких-то событий (например, прихода новой заявки, окончания обслуживания и т.п.).
Математический анализ работы СМО существенно упрощается, если процесс этой работы – марковский.
Случайный процесс называется марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят о того, когда и как система пришла в это состояние.
Пример марковского процесса: процесс игры в шахматы. Пусть s – группа шахматных фигур. Состояние системы характеризуется числом фигур противника на момент 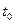 . Вероятность того, что в момент
. Вероятность того, что в момент 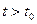 материальный перевес будет на стороне одного из противников, зависит от того, в каком состоянии находится система в данный момент t0, и не зависти от того, когда и в какой последовательности исчезли фигуры с доски до момента t0.
материальный перевес будет на стороне одного из противников, зависит от того, в каком состоянии находится система в данный момент t0, и не зависти от того, когда и в какой последовательности исчезли фигуры с доски до момента t0.
При анализе случайных процессов с дискретными состояниями удобно пользоваться так называемым графом состояний. Обычно состояние системы изображается прямоугольниками (кружками), а возможные переходы из состояния в состояние – стрелками (ориентированными дугами), соединяющими состояния.
Для математического описания марковского случайного процесса с дискретными состояниями и непрерывным временем, протекающего в СМО, рассмотрим более подробно понятие потока событий.
3. Потоки событий (требований)
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (например, потоки вызовов на телефонной станции, поток покупателей и т.п.).
В настоящее время теоретически наиболее разработаны методы решения таких задач СМО, в которых входящий поток требований является простейшим (пуассоновским).
Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т.е. вероятность поступления за время 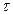 ровно m требований задается формулой
ровно m требований задается формулой
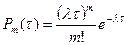 (1)
(1)
Поток характеризуется интенсивностью 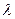 - частотой появления событий или средним числом событий поступающих в СМО в единицу времени
- частотой появления событий или средним числом событий поступающих в СМО в единицу времени
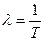 ,
,
где Т – средний интервал времени между соседними поступающими требованиями. Например: Т=3 мин, следовательно, на обслуживание в час прибудет 20 требований
Простейший поток обладает тремя основными свойствами:
- ординарности;
- стационарности;
- отсутствием последействия.
Ординарность потока означает практическую невозможность одновременного поступления двух и более требований.
Стационарным называется поток, у которого вероятностные характеристики не зависят от времени, т.е. интенсивность потока есть величина постоянная. Напомним, что в СМО требования могут поступать через различные промежутки времени, т.е. интервал между соседними поступающими требованиями – величина случайная, и 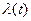 - функция времени.
- функция времени.
Отсутствие последствия означает, что число требований, поступивших в систему до момента t, не определяет того, сколько требований поступит в систему за промежуток от t до 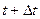 .
.
Важнейшей характеристикой СМО является также время обслуживания требований, поступающих в систему. Время обслуживания одного требования является, как правило, случайной величиной 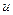 , следовательно, может быть описано законом распределения. Наибольшее распространение получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид
, следовательно, может быть описано законом распределения. Наибольшее распространение получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид
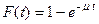 , (2)
, (2)
где 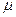 – параметр экспоненциального закона (интенсивность обслуживания), т.е. величина, обратная среднему времени обслуживания
– параметр экспоненциального закона (интенсивность обслуживания), т.е. величина, обратная среднему времени обслуживания