Оптимизация сетевого графика методом «время-стоимость»
Оптимизация сетевого графика в зависимости от полноты решаемой задачи может быть условно разделена на частную и комплексную.
Частная оптимизация – это может быть:
- минимизация времени выполнения при заданной его стоимости;
- минимизация стоимости комплекса работ при заданном времени выполнения проекта.
Комплексная оптимизация – это нахождение оптимального отношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.
При использовании метода «время-стоимость» предполагают, что уменьшение продолжительности работы пропорционально возрастанию его стоимости. Каждая работа (i,j) характеризуется продолжительностью t(i,j), которая может находиться в пределах
,
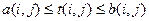где a(i,j) – минимально возможная (экстренная) продолжительность работы (i,j), которую только можно осуществить в условиях разработки;
b(i,j) – нормальная продолжительность выполнения работы (i,j).
При этом стоимость C(i,j) работы (i,j) заключена в границах от Cмин(i,j) (при нормальной продолжительности работы) до Cмак(i,j) (при экстренной продолжительности работы).
Используя аппроксимацию по прямой, можно сравнительно просто найти изменение стоимости работы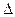 
C(i,j) при сокращении ее продолжительности на величину.
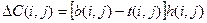
Величина h(i,j) – равна тангенсу угла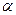 
наклона аппроксимирующей прямой, показывает затраты на ускорение работы (i,j) (по сравнению с нормальной продолжительностью) на единицу времени:
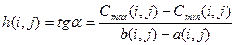
Наиболее очевидный вариант частной оптимизации сетевого графика с учетом стоимости предполагает использование резервов времени работ. Продолжительность каждой работы, имеющей резерв времени, увеличивают до тех пор, пока не будет исчерпан этот резерв или пока не будет достигнуто верхнее значение продолжительности b(i,j). При этом стоимость выполнения проекта, равная до оптимизации:
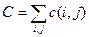
уменьшится на величину
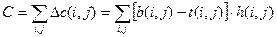
Для проведения частной оптимизации сетевого графика, кроме продолжительности работ t(i,j), необходимо знать их граничные значения a(i,j) и b(i,j), а также показатели затрат на ускорение работ h(i,j)
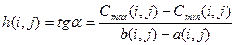
Продолжительность каждой работы t(i,j), целесообразно увеличить на величину такого резерва, чтобы не изменить ранние (ожидаемые) сроки наступления всех событий сети, т.е. на величину свободного резерва времени Rc(i,j).
Тема №3 «Моделирование систем массового обслуживания»
План лекции:
Основные понятия теории массового обслуживания
Понятием Марковского случайного процесса
3. Потоки событий (требований)
Уравнения Колмогорова. Предельные вероятности состояний
Процесс гибели и размножения
СМО с отказами
СМО с очередью
Основные понятия теории массового обслуживания
Во многих областях экономики имеются системы, осуществляющие многократное выполнение однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО). Примерами таких систем можно считать банки, налоговые инспекции, аудиторские службы, системы связи, автозаправочные станции, различные организации и предприятия торгового и бытового обслуживания и т.п.
Каждая СМО состоит из определенного числа обслуживающих единиц (приборов, устройств, пунктов, станций), которые называют каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы, операторы и др. По числу каналов СМО подразделяются на одноканальные и многоканальные.
Заявки поступают в СМО обычно не регулярно, а случайно, образуя так называемый случайный поток заявок (требований). Обслуживание заявок также продолжается какое-то случайное время. Случайный характер потока заявок и времени обслуживания приводит к тому, что СМО оказывается загруженной неравномерно: в какие-то периоды времени скапливается очень большое количество заявок (они либо становятся в очередь, либо покидают СМО не обслуженными), в другие же периоды СМО работает с недогрузкой или простаивает.
Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоками заявок.
В качестве показателей эффективности СМО используются: среднее число заявок, обслуживаемых в единицу времени; среднее число заявок в очереди; среднее время ожидания обслуживания; вероятность отказа в обслуживании без ожидания; вероятность того, что число заявок в очереди превысит определенное значение и т.п.
Цель теории массового обслуживания заключается в разработке рекомендаций по оптимальной организации работы СМО и регулировании потока заявок для обеспечения высокой эффективности их функционирования.
СМО делятся на два основных типа:
- СМО с отказами;
- СМО с ожиданием (очередью).
В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует (например, телефонная станция. Если вызываемы абонент занят, то требование на соединение с ним получает отказ и теряется).
В СМО с ожиданием заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание.