Б. Формирование минимальной потребительской продовольственной корзины

Задан ассортимент продуктов, имеющихся в продаже. Каждый продукт содержит определенное количество разных питательных веществ (витаминов и калорий). Известен требуемый человеку минимум питательных веществ каждого вида. Необходимо определить требуемую потребительскую продовольственную корзину, имеющую минимальную стоимость.

Математическую модель строим по этапам, сформулированным раннее. Задача решается в общем виде, поэтому введем условные обозначения:

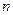- число различных продуктов, имеющихся в продаже;

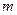- число различных питательных веществ, необходимых человеку;

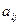- содержание 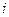-того питательного вещества в 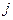-том продукте, , ;

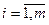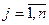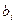- количество 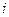-того питательного вещества, необходимое человеку, ;

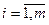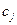- стоимость единицы 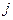- того продукта, .

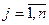Введем управляющие переменные 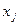- количество 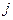- того продукта, входящего в потребительскую корзину, .

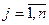Область допустимых решений определяется системой неравенств, содержащей условия по необходимому уровню потребления каждого питательного вещества во всех продуктах и условия неотрицательности управляющих переменных.

Окончательно математическая модель задачи имеет вид:

.

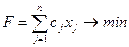
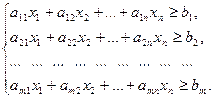
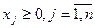4. Система 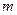линейных уравнений с 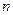переменными

Система 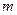линейных уравнений с 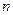переменными имеет вид(6):

,

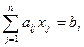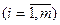
В задачах линейного программирования представляют интерес системы, в которых ранг 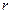матрицы системы 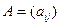, , 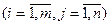или, что то же самое, максимальное число независимых уравнений системы 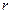меньше числа переменных, т.е. 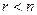. Будем полагать, что в системе (5.6) все 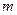уравнений независимы, т.е. 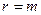и соответственно .

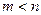Любые 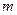переменных системы 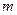линейных уравнений с 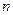переменными 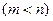называют основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда 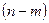переменных называются неосновными (или свободными).

Основными могут быть разные группы из 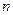переменных. Максимально возможное число групп основных переменных равно числу сочетаний .

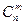Известно, что система 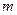линейных уравнений с 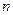переменными может быть как совместной, так и несовместной, а уравнения системы – как зависимыми , так и независимыми.

Несовместность системы означает, что ее уравнения противоречивы. В этом случае система не имеет ни одного решения, а, следовательно, не имеет решения и задача линейного программирования.

Совместная система 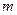линейных уравнений с 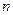переменными 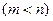имеет бесчисленное множество решений. Среди них выделяют так называемые базисные решения.

Базисным решением системы 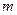линейных уравнений с 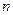переменными называется решение, в котором все 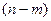неосновных переменных равны нулю.

В задачах линейного программирования особый интерес представляют допустимые базисные решения или как их еще называют опорные планы.

Допустимым базисным решением является решение, содержащее 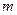неотрицательных основных (базисных) переменных и 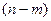неосновных (или свободных) переменных, которые в базисном решении равны нулю. Основные же переменные, как правило, отличны от нуля, т.е. являются положительными числами.

Если хотя бы одна из основных переменных принимает нулевое значение, то соответствующее базисное решение называется вырожденным.

Так как компоненты оптимального решения задачи линейного программирования не могут быть отрицательными, то поиск этого решения нужно ограничить только допустимыми решениями системы ограничений. Но как найти это оптимальное решение среди бесчисленного множества допустимых решений системы ограничений? Перебирать их очень трудоемко, поэтому необходимо выработать схему, по которой переход от одного допустимого решения к следующему обязательно сопровождался бы не уменьшением значения функции цели .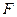

Для этой цели необходимо рассмотреть ряд понятий, построенных на геометрии так называемых выпуклых множеств.

Геометрия выпуклых множеств

Множество, элементами которого являются точки, называется точечным. Примерами точечных множеств на плоскости являются: треугольник, угол, точки прямой (или прямая), отрезок, луч, круг и т.д. В пространстве – параллелепипед, призма, шар и т.п.

Различают выпуклые и невыпуклые точечные множества.

Определение.Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий их.

В противном случае множество называется невыпуклым (рис. 1)

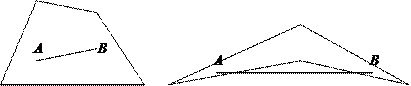
выпуклое невыпуклое

Рис. 5.1

Выпуклые множества обладают важным свойством: пересечение (общая часть) двух выпуклых множеств также выпуклое множество.

Точка выпуклого множества называется угловой (или крайней), если через нее нельзя провести ни одного отрезка, состоящего только из точек данного множества и для которого она была бы внутренней.

Для выпуклого многоугольника угловыми точками являются все его вершины, для отрезка – его концы.

Рассмотрим геометрическую интерпретацию множества допустимых решений системы линейных уравнений на конкретном примере.

Дано уравнение 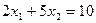. Рассматривая уравнение как систему, состоящую из одного уравнения с двумя неизвестными, найти:

- множество допустимых решений;

- угловые точки этого множества;

- базисные решения.

Решение. Каждое решение данного уравнения – пара чисел, а геометрически – точка на плоскости. Множество всех его решений – прямая. Неотрицательным решениям данной системы (состоящей из одного уравнения) соответствуют точки отрезка АВ, т.е. выпуклое множество с двумя угловыми точками А и В (рис. 2). Итак, множеством допустимых решений системы из одного уравнения с двумя переменными оказался выпуклый многоугольник.

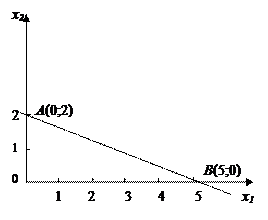
Рис. 2

Найдем базисные решения системы. Принимая х₁ за основную переменную (тогда х₂ – неосновная) и полагая в уравнении х₂=0, получим х₁=5. Первое базисное решение (5;0).

Если за основную переменную принять х₂, то получим второе базисное решение (0;2). Оба базисных решения допустимы. Им соответствуют угловые точки множества допустимых решений системы (рис. 5.2).

Еще пример. Дано уравнение 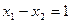. Строим прямую по данному уравнению (рис. 3).

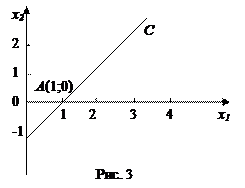
Координаты ее точек служат решениями этого уравнения. Неотрицательным решениям соответствуют точки луча АС – выпуклого множества с одной угловой точкой А(1;0). Найдем базисные решения системы. Если принять х₁ за основную переменную, то получим базисное решение (1;0). Если же за основную переменную примем х₂, то второе базисное решение (0;-1) не является допустимым.

Обратим внимание на то, что между угловыми точками и допустимыми базисными решениями системы существует однозначное соответствие: число угловых точек множества равно числу допустимых базисных решений системы. Оказывается, эта закономерность носит общий характер.

Теперь рассмотрим геометрическую интерпретацию множества решений линейного неравенства с двумя переменными.

В общем виде линейное неравенство с двумя переменными записываются в виде

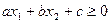(8)

или

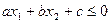(9)

Каждому решению неравенств, т.е. паре чисел (х₁, х₂) соответствует точка на плоскости, а множеством решений линейного неравенства (8) служит одна из двух полуплоскостей, на которую всю плоскость делит прямая 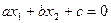, включая и эту прямую, а другая полуплоскость вместе с прямой является множеством решений неравенства (9).

Рассмотрим ряд примеров.

Пример 1. Построить множество решений неравенства .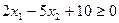

Решение. Искомое множество решений состоит из решений уравнения 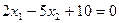и строгого неравенства 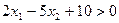. Решениями уравнения служат точки прямой 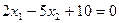, которая построена на рис.4.

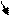
Множество решений строгого неравенства – одна из плоскостей, на которые делит плоскость прямая АВ. Какая из них является искомой, выясняют с помощью контрольной точки, в качестве которой удобно брать начало координат. Действительно, подставляя в неравенство координаты начала координат, получим 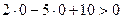, т.е. оно выполняется. Следовательно, множеством решений строгого неравенства служит нижняя полуплоскость, т.к. она содержит начало координат, а решением исходного неравенства – полуплоскость вместе с прямой.

Пример 2. Построить множество решений системы линейных неравенств

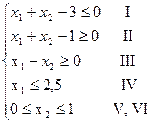
Решение.

1) Строим прямую 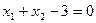. Подстановка начала координат как контрольной точки дает -3<0, т.е. оно выполняется. Множество решений первого неравенства – нижняя полуплоскость вместе с прямой I.

2) Строим прямую 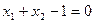и множество решений второго неравенство это верхняя полуплоскость с прямой II.

3) Строим прямую 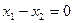. Она проходит через начало координат (в уравнении отсутствует свободный член). Вторую точку найдем, полагая, например, 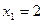, тогда 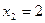. В качестве контрольной точки возьмём точку (0;2). Множество решений неравенства – нижняя полуплоскость с прямой III.

4) Строим прямую 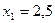. Значение 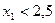лежит левее этой прямой, что и определяет полуплоскость решений неравенства .

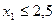5) Двойное неравенство 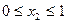эквивалентно системе двух неравенств 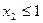и 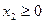. Неравенству 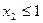соответствует полуплоскость, расположенная ниже прямой 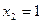; соответственно для 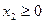– полуплоскость, лежащая выше оси абсцисс (рис. 5).

Следовательно, множество решений системы из всех пяти неравенств – выпуклый многоугольник ABCDEF с конечным числом угловых точек. Координаты точек A, B, C, D, E, F могут быть найдены как координаты пересечения соответствующих прямых. Например, точка А является точкой пересечения прямых I и V. Решая совместно уравнения этих прямых, получим

;

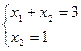
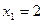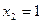
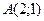
В заключение сформулируем основные теоремы линейного программирования, базирующиеся на геометрии выпуклых множеств.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

Теорема 2. Если существует, и притом единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений.

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений системы ограничений, и наоборот, каждой угловой точке множества допустимых решений системы ограничений соответствует допустимое базисное решение.