Продуктивная модель Леонтьева

Матрица называется продуктивной, если для любого вектора существует решение уравнение (3).

В этом случае и модель Леонтьева, определяемая матрицей , также называется продуктивной.

Существует несколько критериев продуктивности матрицы . Приведем некоторые из них.

1. Матрица продуктивна тогда и только тогда, когда матрица существует и неотрицательна.

Пример. Исследовать на продуктивность матрицу

Решение. Матрица ;

, следовательно, матрица не вырождена и имеет обратную

.

Напомним, что , где , , , - алгебраические дополнения элементов матрицы .

Как видно, матрица существует и неотрицательна. Следовательно, матрица продуктивна.

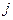2. Матрица продуктивна, если максимум сумм элементов её столбцов не превосходит единицы, причем, хотя бы для одного из столбцов сумма элементов, строго меньше единицы, т.е. матрица продуктивна, если для любых и , и существует номер такой, что .

Пример. Исследовать на продуктивность матрицу

Решение. Элементы матрицы имеют неотрицательные элементы и удовлетворяют критерию продуктивности:

.

Следовательно, матрица продуктивна.

Примеры решения задач межотраслевого баланса

Пример 1. В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.

Отрасль	Потребление	Конечный продукт
промышленность	Сельское хозяйство
производство	Промышленность	0,3	0,25
Сельское хозяйство	0,15	0,12

Найти:

а) плановые объемы валовой продукции отраслей, межотраслевые поставки, чистую продукцию отраслей;

б) необходимый объем валового выпуска каждой отрасли, если конечное потребление продукции сельского хозяйства увеличится на 20%, а промышленности на 10%.

Решение. Матрица коэффициентов прямых затрат и вектор конечной продукции имеют вид:

, .

Найдем матрицу

Матрица полных затрат равна:

.

По формуле (6.5) вычислим вектор валового продукта :

.

Межотраслевые поставки 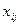найдем по формуле (6.2)

.

; ;

; .

Найдем чистую продукцию отраслей.

Чистой продукцией отраслей называется разность между валовой продукцией этой отрасли и затратами продукции всех отраслей на производство этой отрасли.

Для промышленности и сельского хозяйства она соответственно равна:

,

.

По условию вектор конечного потребления продукции промышленности увеличится на 10%, а сельского хозяйства на 20%

.

Тогда вектор валового продукта будет равен:

.

Таким образом, выпуск в промышленности нужно увеличить до 532,8 усл.ден.ед., а в сельском хозяйстве – до 287,1 усл.ден.ед.

Пример 2. Дана матрица прямых затрат .

Найти: а) вектор валовой продукции для обеспечения выпуска конечной продукции ;

б) приращение вектора для увеличения выпуска конечной продукции на .

Решение. а) Матрица

Вектор валовой продукции равен:

.

б) Так как , то вектор выпуска конечной продукции равен .

Вектор валовой продукции при этом равен

.

Следовательно, приращение вектора равно .

Пример 3. Работа системы, состоящей из двух отраслей, в течение некоторого периода характеризуется следующими данными (усл.ден.ед.):

Отрасль	потребление	Чистая продукция
I	II
I
II

Вычислить матрицу прямых затрат.

Решение. Чистая продукция отраслей равна соответственно

Где - валовой продукт отраслей I и II.

Отсюда, , .

Межотраслевые поставки определяются по формулам ,откуда

,

, .

Таким образом, матрица прямых затрат имеет вид: .

Тема №2 «Методы оптимизации планирования и управления»

План лекции: