Многомерное нормальное распределение
Плотность нормального распределения имеет вид
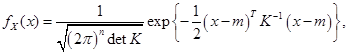 (3.26)
(3.26)
где 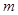 - вектор математического ожидания случайного вектора X;
- вектор математического ожидания случайного вектора X;
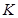 - ковариационная матрица случайного вектора X;
- ковариационная матрица случайного вектора X;
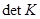 - определитель ковариационной матрицы.
- определитель ковариационной матрицы.
Если раскрыть квадратичную форму в фигурных скобках выражения (3.26), то плотность нормального закона можно записать в виде
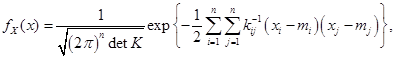 (3.27)
(3.27)
где 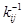 - элементы матрицы, обратной по отношению к ковариационной матрице
- элементы матрицы, обратной по отношению к ковариационной матрице 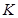 случайного вектора
случайного вектора 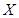 ;
; 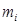 - математическое ожидание величины
- математическое ожидание величины 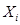 ;
;
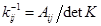 ;
;
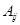 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 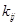 матрицы ковариации
матрицы ковариации 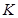 .
.
В силу симметрии ковариационной матрицы 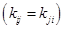 , обратная ковариационная матрица также обладает свойством симметрии:
, обратная ковариационная матрица также обладает свойством симметрии:
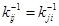
Таким образом, для описания нормального закона распределения системы п случайных величин нужно знать следующие величины:
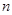 математических ожиданий:
математических ожиданий: 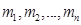 ;
; 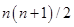 элементов ковариационной матрицы (из которых
элементов ковариационной матрицы (из которых 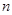 дисперсий).
дисперсий).
На главной диагонали ковариационной матрицы 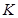 стоят дисперсии случайных величин.
стоят дисперсии случайных величин.
Если нормально распределенные СВ 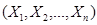 не коррелированы, то ковариационная матрица становится диагональной:
не коррелированы, то ковариационная матрица становится диагональной:
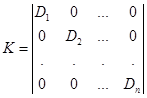
В этом случае определитель 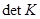 будет равен произведению диагональных элементов:
будет равен произведению диагональных элементов:
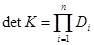 ,
,
а обратная ковариационная матрица также будет диагональной:
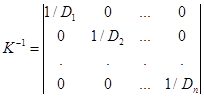
Следовательно, для нормально распределенной системы некоррелированных СВ совместная плотность имеет вид:
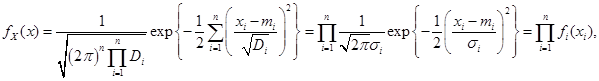 (3.28)
(3.28)
где 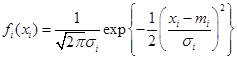
Как следует из (3.28)нормально распределенная система некоррелированных случайных величин 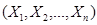 представляет собой нормально распределенную системунезависимых случайных величин,так как совместная плотность
представляет собой нормально распределенную системунезависимых случайных величин,так как совместная плотность 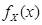 системы
системы 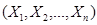 равна произведению плотностей отдельных величин
равна произведению плотностей отдельных величин 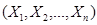 , входящих в систему. Таким образом, для нормально распределенной системы п СВ из некоррелированности отдельных величин следует их независимость.
, входящих в систему. Таким образом, для нормально распределенной системы п СВ из некоррелированности отдельных величин следует их независимость.
Любая подсистема случайных величин 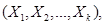 входящая в нормально распределенную систему
входящая в нормально распределенную систему 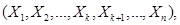 также распределена по нормальному закону, зависящему от
также распределена по нормальному закону, зависящему от 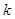 математических ожиданий и
математических ожиданий и 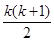 элементов ковариационной матрицы.
элементов ковариационной матрицы.
Можно определить условную плотность распределения подсистемы СВ 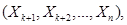 вычисленную при условии, что остальные случайные величины
вычисленную при условии, что остальные случайные величины 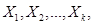 входящие в систему, приняли определенные значения:
входящие в систему, приняли определенные значения: 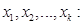
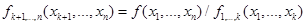 , (3.29)
, (3.29)
где 
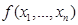 -нормальная плотность распределения системы случайных величин
-нормальная плотность распределения системы случайных величин 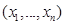 ,
,
определяемая по формуле (2.28); 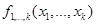 - нормальная плотность распределения подсистемы случайных величин
- нормальная плотность распределения подсистемы случайных величин 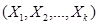 . При этом закон распределения (2.29) будет тоже нормальным.
. При этом закон распределения (2.29) будет тоже нормальным.
В инженерных приложениях чаще всего имеют дело с условным законом распределения случайной величины 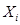 вычисленным при условии, что остальные случайные величины, входящие в систему, приняли определенные значения:
вычисленным при условии, что остальные случайные величины, входящие в систему, приняли определенные значения: 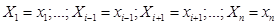 . Этот условный закон будет нормальным с характеристиками
. Этот условный закон будет нормальным с характеристиками
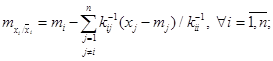 (3.30)
(3.30)
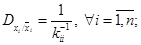 (3.31)
(3.31)
где 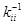 - элемент матрицы
- элемент матрицы 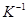 , обратной по отношению к ковариационной матрице
, обратной по отношению к ковариационной матрице 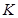 .
.
Условное математическое ожидание 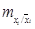 представляет собой линейную функцию (п—1) переменных
представляет собой линейную функцию (п—1) переменных 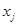
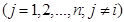 , поэтому поверхность регрессии
, поэтому поверхность регрессии 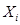 на
на 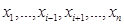 представляет собой гиперплоскость в
представляет собой гиперплоскость в 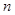 -мерном пространстве.
-мерном пространстве.
Условная плотность распределения СВ 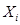 , при условии, что
, при условии, что 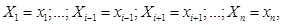 равна
равна
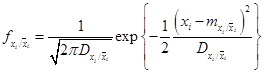 (3.32)
(3.32)
Вероятность попадания случайной точки 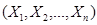 в n – мерный прямоугольный параллелепипед Rn со сторонами, параллельными координатным осям выражается через функцию Лапласа:
в n – мерный прямоугольный параллелепипед Rn со сторонами, параллельными координатным осям выражается через функцию Лапласа:
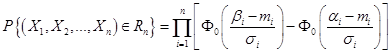 (3.33)
(3.33)
где 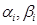 — координаты границ прямоугольного параллелепипеда Rn в направлении оси
— координаты границ прямоугольного параллелепипеда Rn в направлении оси 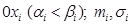 — м. о. и с к о- случайной величины
— м. о. и с к о- случайной величины 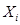 , Ф0 (z)—функция Лапласа.
, Ф0 (z)—функция Лапласа.
Если нормально распределенные СВ независимы (не коррелированы) и при этом 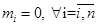 , то их плотность распределения может быть записана в виде:
, то их плотность распределения может быть записана в виде:
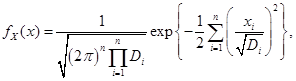 (3.34)
(3.34)
которая называется канонической (простейшей) формой нормального закона системы п СВ 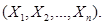 Найдем уравнение
Найдем уравнение 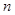 -мерного гиперэллипсоида равной плотности, в который попадает случайная точка
-мерного гиперэллипсоида равной плотности, в который попадает случайная точка 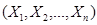 . Уравнение гиперэллипсоида можно получить из условия:
. Уравнение гиперэллипсоида можно получить из условия:
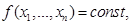
откуда
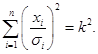 (3.35)
(3.35)
При п = 2 получаем уравнение эллипса равной плотности в декартовой прямоугольной системе координат на плоскости 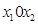
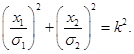 (3.36)
(3.36)
Центр этого эллипса находится в начале координат, его полуоси равны: 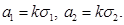
Найдем вероятность попадания СВ 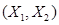 в область
в область 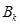 , ограниченную эллипсом (3.36).
, ограниченную эллипсом (3.36).
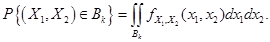
Для вычисления интеграла перейдём к полярной системе координат 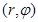 :
:
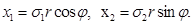
Якобиан этого преобразования 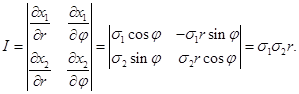 Тогда
Тогда 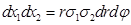 . При этом уравнение эллипса преобразуется в уравнение окружности радиуса
. При этом уравнение эллипса преобразуется в уравнение окружности радиуса 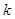 . Следовательно
. Следовательно
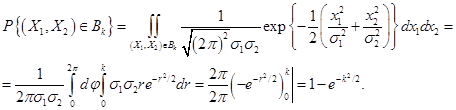
Лекция 4. Числовые характеристики и законы распределения функций случайных величин. Характеристические функции. Линеаризация функций случайных величин
1. Числовые характеристики функций случайных величин.Если 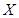 — дискретная или непрерывная случайная величина с известным законом распределения и
— дискретная или непрерывная случайная величина с известным законом распределения и 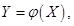 где
где 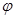 — неслучайная функция, то математическое ожидание и дисперсия случайной величины
— неслучайная функция, то математическое ожидание и дисперсия случайной величины 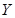 в случае, если они существуют, могут быть найдены по формулам
в случае, если они существуют, могут быть найдены по формулам
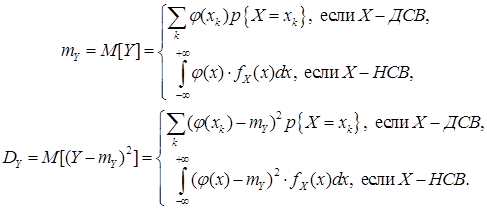 (4.1)
(4.1)
Аналогичные формулы имеют место и для всех прочих начальных и центральных моментов распределения случайной величины 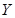 , которая является неслучайной функцией
, которая является неслучайной функцией 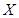 . Таким образом, для вычисления числовых характеристик неслучайной функции случайной величины не надо знать закона распределения зависящей от X случайной величины Y, а достаточно знать закон распределения случайного аргумента X. Сформулированное правило естественно обобщается на функции от большего числа случайных переменных. Например, если
. Таким образом, для вычисления числовых характеристик неслучайной функции случайной величины не надо знать закона распределения зависящей от X случайной величины Y, а достаточно знать закон распределения случайного аргумента X. Сформулированное правило естественно обобщается на функции от большего числа случайных переменных. Например, если 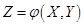 , то
, то
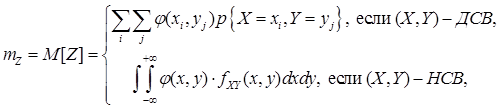 (4.2)
(4.2)
Если существуют соответствующие моменты, то справедливы следующие свойства математического ожидания и дисперсии:
- Для любых случайных величин
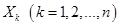
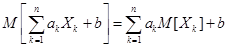 - свойство линейности. (4.3)
- свойство линейности. (4.3)
- Для любых случайных величин
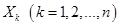

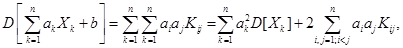 (4.4)
(4.4)
где 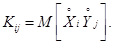
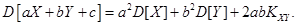
-
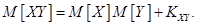 (4.5)
(4.5) -
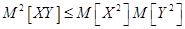 - неравенство Коши-Буняковского.
- неравенство Коши-Буняковского. - Если
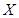 и
и 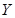 независимы, то
независимы, то
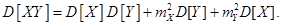 (4.6)
(4.6)
Свойство 1 может быть записано в более общей форме в матричных обозначениях:
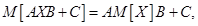 (4.7)
(4.7)
где X — случайный n-мерный вектор-столбец, 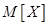 — неслучайный
— неслучайный 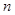 -мерный вектор-столбец, компоненты которого равны математическим ожиданиям случайных компонент вектора X,
-мерный вектор-столбец, компоненты которого равны математическим ожиданиям случайных компонент вектора X,
А, В и С — постоянные матрицы порядков соответственно