Градиенты силы притяжения и вторые производные гравитационного потенциала
В теории гравитационного потенциала рассматривается градиент вектора ускорения силы притяжения (для точек земной поверхности – силы тяжести), т.е. градиент градиента потенциала этой силы, вследствие чего результат такого рода операции согласно (11) представляет собой симметричную матрицу. В спутникоцентрической правой горизонтной системе координат 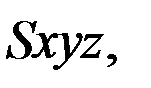 ось
ось 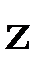 которой направлена к центру масс Земли, а ось
которой направлена к центру масс Земли, а ось 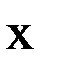 устремлена в северном направлении параллельно касательной к меридиану подспутниковой точки, матрица вторых производных гравитационного потенциала
устремлена в северном направлении параллельно касательной к меридиану подспутниковой точки, матрица вторых производных гравитационного потенциала
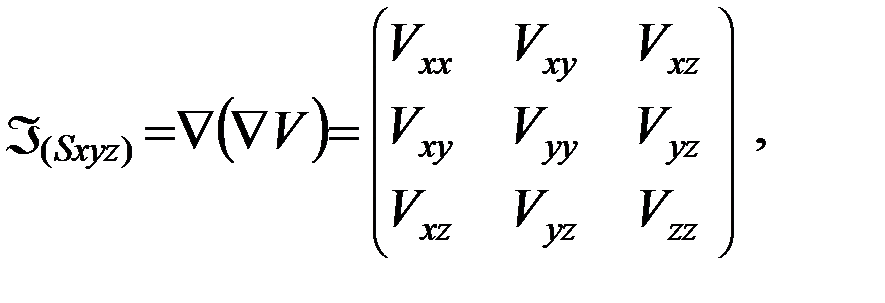 (12)
(12)
включает пять независимых элементов, поскольку во внешнем не занятом притягивающими массами пространстве потенциал ньютоновской силы притяжения обладает свойством гармоничности, т.е выполняется условие:
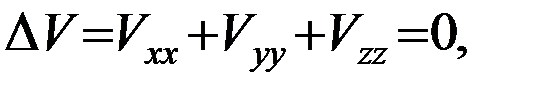 где
где 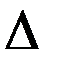 - оператор Лапласа. Для точек, расположенных на поверхности Земли, имеет место равенство
- оператор Лапласа. Для точек, расположенных на поверхности Земли, имеет место равенство
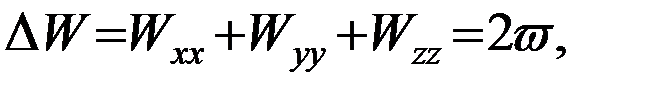 где W - потенциал силы тяжести, а
где W - потенциал силы тяжести, а
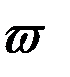 - угловая скорость вращения Земли.
- угловая скорость вращения Земли.
Заметим в этой связи, что градиентометрия есть, по-видимому, область наиболее наглядного проявления теснейшей связи гравитации и геометрии пространства, находящей свое отражение в свойствах матрицы-тензора (12). Дело в том, что каждый из элементов этой матрицы характеризует ту или иную особенность геометрии уровенных поверхностей и силовых линий гравитационного поля исследуемого небесного тела. Так, в частности, производные 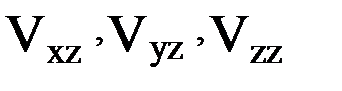 представляют собой компоненты вектора – градиента ньютоновской силы притяжения, поскольку
представляют собой компоненты вектора – градиента ньютоновской силы притяжения, поскольку
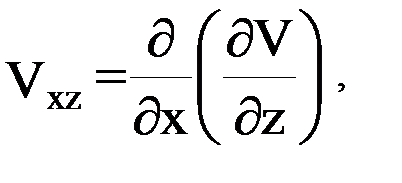
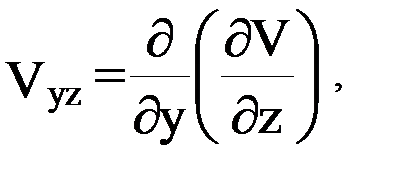
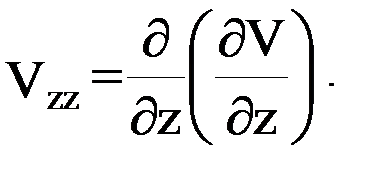
Если направление оси 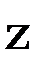 совпадает с нормалью к уровенной поверхности потенциала силы притяжения (для точек поверхности Земли – к геоиду), то горизонтальная плоскость, содержащая оси
совпадает с нормалью к уровенной поверхности потенциала силы притяжения (для точек поверхности Земли – к геоиду), то горизонтальная плоскость, содержащая оси 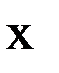 и
и 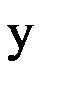 , будет представлять собой плоскость, касательную к указанной уровенной поверхности. Тогда производные
, будет представлять собой плоскость, касательную к указанной уровенной поверхности. Тогда производные 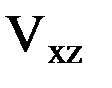 и
и 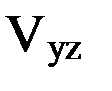 характеризуют изменения силы притяжения в горизонтальной плоскости в направлении меридиана и первого вертикала подспутниковой точки соответственно, вследствие чего часто называются горизонтальными градиентами. Производная
характеризуют изменения силы притяжения в горизонтальной плоскости в направлении меридиана и первого вертикала подспутниковой точки соответственно, вследствие чего часто называются горизонтальными градиентами. Производная 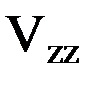 отражает изменение силы притяжения вдоль вертикальной оси и потому носит название вертикального градиента. Полным горизонтальным градиентом называется вектор
отражает изменение силы притяжения вдоль вертикальной оси и потому носит название вертикального градиента. Полным горизонтальным градиентом называется вектор 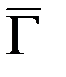 , совпадающий с направлением максимального изменения силы притяжения в плоскости горизонта – азимут этого направления обозначим
, совпадающий с направлением максимального изменения силы притяжения в плоскости горизонта – азимут этого направления обозначим 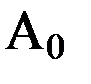 . Тогда
. Тогда
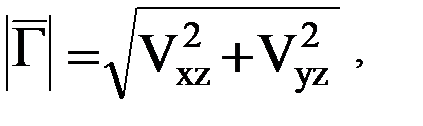
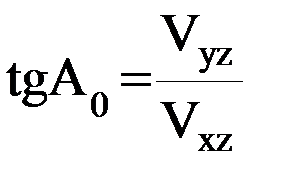 . (13)
. (13)
Вторые производные 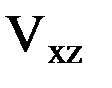 и
и 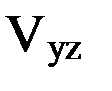 описывают кривизну силовой линии гравитационного поля. Напомним, что кривизной некоторой кривой называется предел отношения угла между направлениями касательных к кривой в двух близких точках к длине кривой между этими точками. В согласии с этим определением для кривизны
описывают кривизну силовой линии гравитационного поля. Напомним, что кривизной некоторой кривой называется предел отношения угла между направлениями касательных к кривой в двух близких точках к длине кривой между этими точками. В согласии с этим определением для кривизны 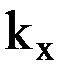 проекции силовой линии на плоскость меридиана можем записать:
проекции силовой линии на плоскость меридиана можем записать:
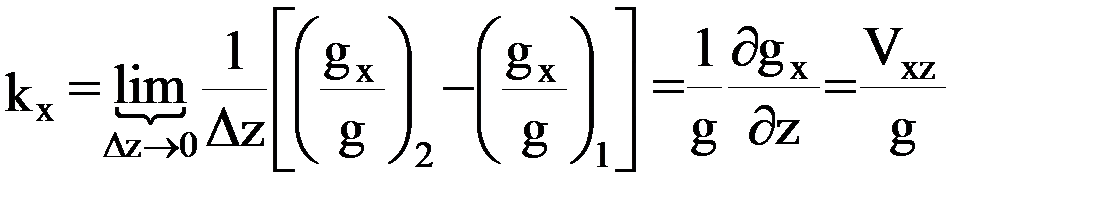 ,
,
где 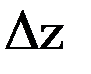 – длина силовой линии между точками 1 и 2. Для кривизны
– длина силовой линии между точками 1 и 2. Для кривизны 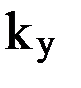 - проекции силовой линии поля на плоскость первого вертикала аналогичное равенство имеет вид:
- проекции силовой линии поля на плоскость первого вертикала аналогичное равенство имеет вид: 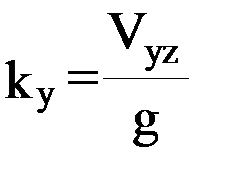 . Величина обратная кривизне называется радиусом кривизны кривой. Известно, что радиус
. Величина обратная кривизне называется радиусом кривизны кривой. Известно, что радиус 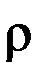 кривизны уровенной поверхности геоида в плоскости нормального сечения его в азимуте
кривизны уровенной поверхности геоида в плоскости нормального сечения его в азимуте 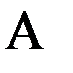 определяется, исходя из равенства,
определяется, исходя из равенства,
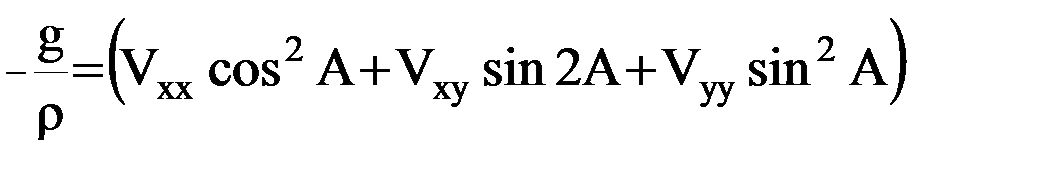 , (14)
, (14)
где символом 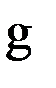 обозначена сила тяжести (на спутниковых высотах – сила притяжения). Если в (14) принять
обозначена сила тяжести (на спутниковых высотах – сила притяжения). Если в (14) принять 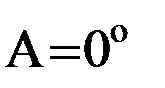 , то
, то 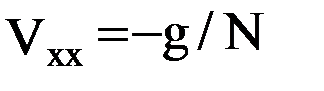 , а при
, а при 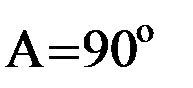
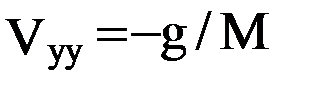 , где
, где 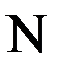 и
и 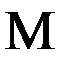 суть радиусы кривизны сечения геоида в плоскостях меридиана и первого вертикала. Это означает, что производные
суть радиусы кривизны сечения геоида в плоскостях меридиана и первого вертикала. Это означает, что производные 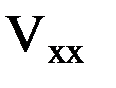 и
и 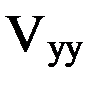 характеризуют кривизну нормального сечения уровенной поверхности потенциала силы притяжения (на поверхности Земли – уровенной поверхности потенциала силы тяжести, т.е. геоида).
характеризуют кривизну нормального сечения уровенной поверхности потенциала силы притяжения (на поверхности Земли – уровенной поверхности потенциала силы тяжести, т.е. геоида).
Обозначим через 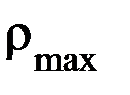 и
и 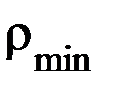 радиусы кривизны главных нормальных сечений, имеющих минимальную и максимальную кривизну соответственно. Найдем азимуты направлений
радиусы кривизны главных нормальных сечений, имеющих минимальную и максимальную кривизну соответственно. Найдем азимуты направлений 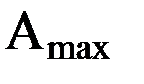 и
и 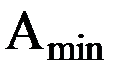 , им соответствующие, называемые также азимутами направлений главных нормальных сечений. С этой целью исследуем правую часть равенства (14) на экстремум на множестве значений
, им соответствующие, называемые также азимутами направлений главных нормальных сечений. С этой целью исследуем правую часть равенства (14) на экстремум на множестве значений 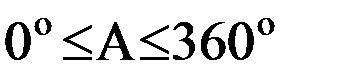 , приравнивая производную по
, приравнивая производную по 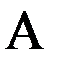 нулю. Имеем:
нулю. Имеем:
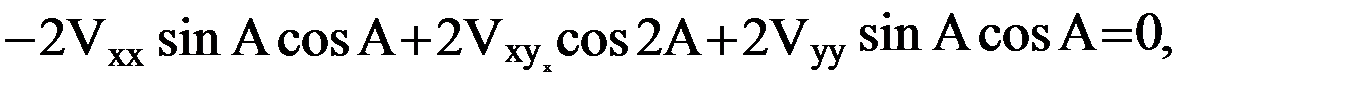
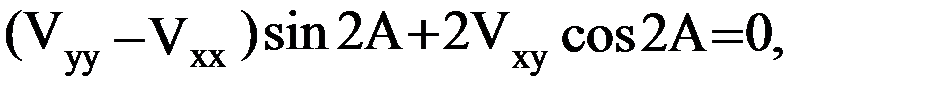
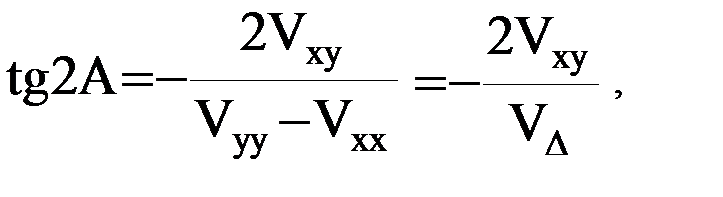 (15)
(15)
где обозначено 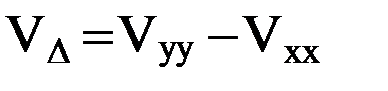 . Решение тригонометрического уравнения (15) дает значения азимутов
. Решение тригонометрического уравнения (15) дает значения азимутов 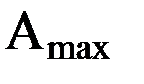 и
и 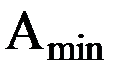 , различающиеся на
, различающиеся на 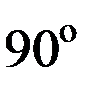 .
.
Размерность вторых производных гравитационного потенциала соответствует размерности производной силы притяжения по некоторому направлению, т.е. 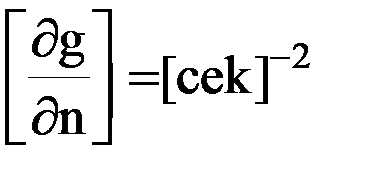 . Это очень крупная единица, на несколько порядков превышающая величины вторых производных, характерные для Земли и других планет. По этой причине в качестве единицы измерения используется одна миллиардная этой величины, называемая Этвеш (1 Этвеш =
. Это очень крупная единица, на несколько порядков превышающая величины вторых производных, характерные для Земли и других планет. По этой причине в качестве единицы измерения используется одна миллиардная этой величины, называемая Этвеш (1 Этвеш = 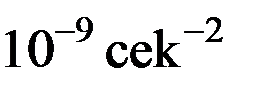 ), в честь венгерского физика Р.фон Этвеша, разработавшего конструкцию прибора для измерения вторых производных потенциала силы тяжести – гравитационного вариометра [2]. В частности, для модели однородной сферической Земли вторые производные гравитационного потенциала имеют следующие числовые значения:
), в честь венгерского физика Р.фон Этвеша, разработавшего конструкцию прибора для измерения вторых производных потенциала силы тяжести – гравитационного вариометра [2]. В частности, для модели однородной сферической Земли вторые производные гравитационного потенциала имеют следующие числовые значения:
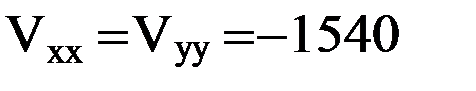 Э,
Э, 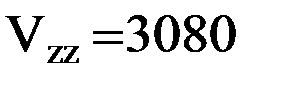 Э,
Э, 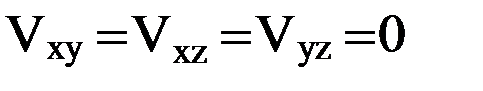 Э.
Э.
