Уравнения наблюдений и уравнения поправок спутниковой градиентометрии

Напомним, что в современной геодезической литературе рассматриваются два подхода к оцениванию параметров гравитационного потенциала исследуемого небесного тела по спутниковым данным: пространственный (space-wise) и временной (time-wise) [1]. В рамках пространственного подхода результат измерения на околоземной орбите некоторой второй производной 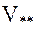геопотенциала представим в виде функционала :

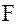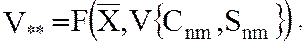(32)

зависящего от 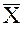– геоцентрического вектора состояния ИСЗ и 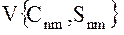- потенциала силы притяжения Земли, описываемого набором гармонических коэффициентов разложения его в ряд объемных сферических функций:

.

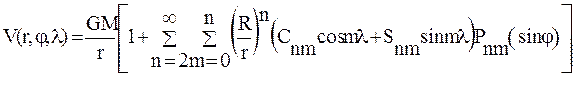Выражение (в1) называется уравнением наблюдений, устанавливающим функциональную связь измеряемой величины с набором подлежащих определению параметров модели гравитационного потенциала.

Линеаризация уравнения наблюдений (32) в окрестности априорно приближенно известных (референцных) значений неизвестных позволяет получить уравнение поправок:

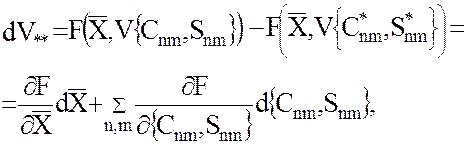(33)

где 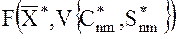есть референцное значение измеряемой производной 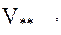вычисляемое по референцному значению 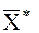вектора и набору заранее приближенно известных значений 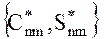параметров модели гравитационного поля Земли. Искомыми неизвестными в (33) являются поправки 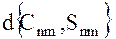, имеющие смысл либо поправок в заранее приближенно известные значения коэффициентов 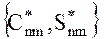референцной модели потенциала, либо неизвестных коэффициентов старших по сравнению референцной моделью степеней и порядков.

Использование в качестве модели геопотенциала его разложения в ряд (6) объемных сферических функций диктует необходимость представления уравнений наблюдений спутниковой градиентометрии в форме (32). Для этого выразим уравнения (29) в сферических координатах, проводя непосредственное дифференцирование ряда (6). В результате получим следующие формулы для уравнений наблюдений в спутникоцентрической горизонтной системе координат .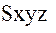

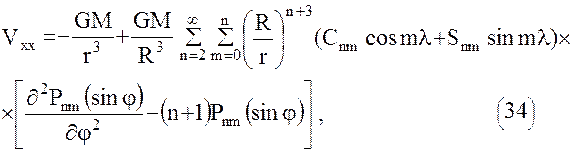
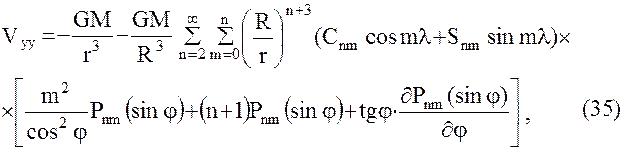
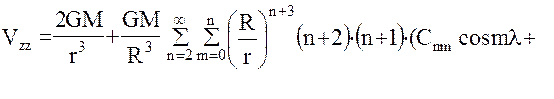
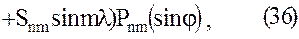
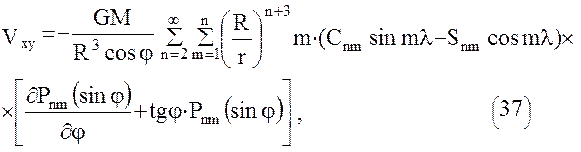
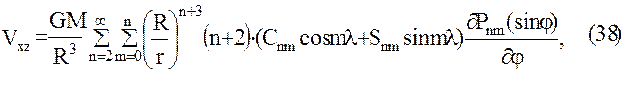
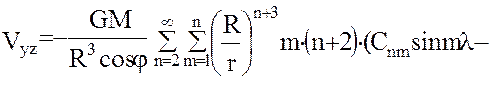
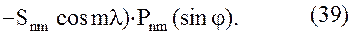
Поскольку для точек внешнего не занятого притягивающими массами пространства уравнение Лапласа справедливо в любой прямоугольной системе координат, имеем: 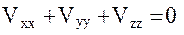, что дает возможность проконтролировать вывод формул (34), (35), (36).

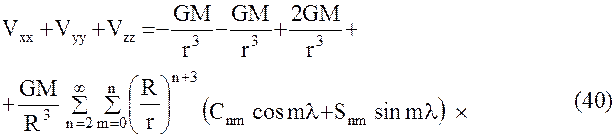
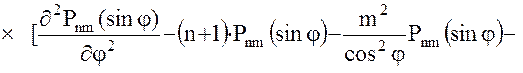
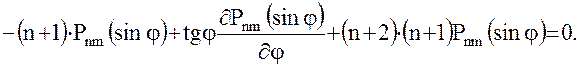
Очевидно, правильность формул можно будет считать доказанной в случае равенства нулю в выражении (40) квадратной скобки. Это легко сделать, воспользовавшись известными соотношениями для производных присоединенных функций Лежандра:

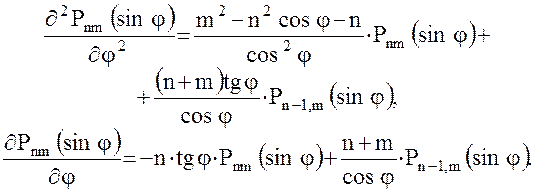
Коэффициенты уравнений поправок (33) для уравнений наблюдений

(34) – (39) вычисляются по формулам:

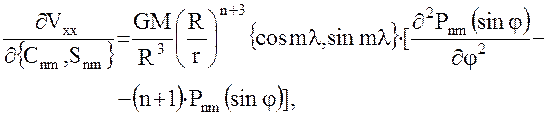(41)

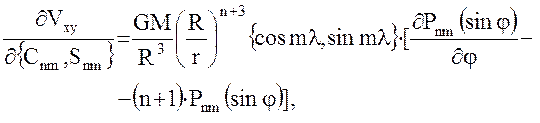(42)

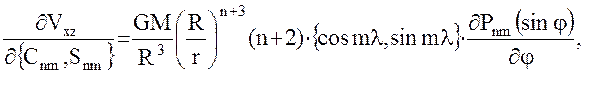
(43)

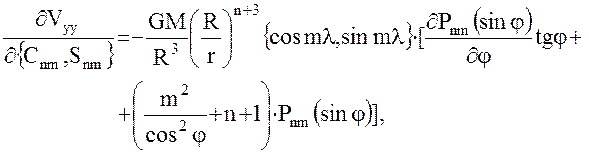
(44)

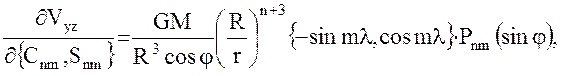(45)

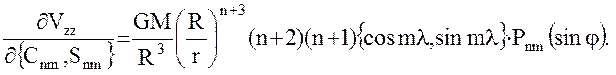
(46)

Аналогичные выкладки несложно выполнить и в спутникоцентрической орбитальной системе координат 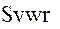, рассматривая в качестве исходных уравнений наблюдений уравнения (31).

Принципы измерения вторых производных гравитационного потенциала

В классической наземной гравиметрии главной измеряемой величиной является модуль вектора силы тяжести – первая нормальная производная соответствующего потенциала. Известно, однако, что, повышая порядок измеряемой производной, возможно добиться относительного увеличения амплитуды коротковолновой компоненты поля, вследствие чего последняя определяется более уверенно. Вот почему, как уже указывалось выше, для оценивания параметров высокочастотной (т.е. коротковолновой) составляющей гравитационного поля, описывающих по мере возрастания степени вычисляемых гармоник все более мелкие особенности его структуры, выгоднее использовать измерения вторых производных потенциала ньютоновской силы притяжения.

Рассмотрим основные принципы бортовых измерений вторых производных гравитационного потенциала. Покажем, что градиентометрические измерения представляют собой измерения характеристик относительного движения элементов динамической системы пробных масс инструмента-градиентометра.

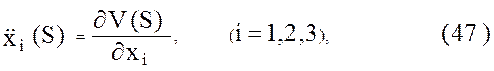Пусть в произвольной спутникоцентрической прямоугольной системе координат 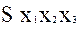положение точки описывается трехмерным вектором 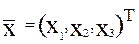. Тогда в отсутствии влияния сил негравитационной природы имеем:

где 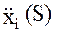– составляющая ньютоновской силы притяжения по i-ой оси в точке 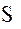, 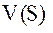– потенциал силы притяжения в той же точке. Запишем (47) для некоторой точки 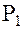, близкой к 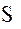, и разложим в ряд Тейлора в окрестности точки :

.

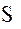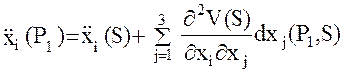Аналогично для точки :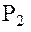

.

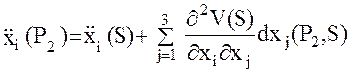Относительное ускорение единичных пробных масс, находящихся в точках

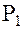и 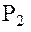, запишем в виде разности:

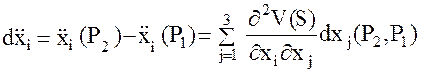, (48)

где принято 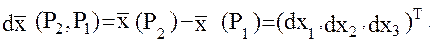Таким образом, в соответствии с (2) измерение вторых производных 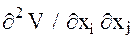сводится к измерению компонент 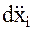вектора 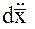относительного ускорения и компонент 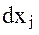вектора 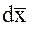относительного положения пробных масс спутникового градиентометра. Компоненты 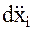вектора относительных ускорений 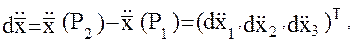действующих на каждую из разнесенных в пространстве пробных масс, измеряются с помощью трехкомпонентного акселерометра, принцип действия которого может быть описан следующим образом. Пусть внутри движущегося объекта на пружинных подвесах, имеющих лишь одну степень свободы перемещения вдоль оси 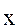, установлены два идентичных пробных тела единичной массы (рис.2а). При движении в однородном гравитационном поле и отсутствии негравитационных возмущений на оба тела (и на объект-носитель) будут действовать одинаковые ускорения. Это означает, что пробные тела будут находиться на не меняющемся со временем расстоянии друг от друга, а их относительные ускорения будут равны нулю. Тогда в соответствии с (2) будут равны нулю и все вторые производные поля (напомним, что в данном случае нами рассматривается движение в однородном поле).

В неоднородном гравитационном поле на пробные массы в каждый момент времени будут действовать ускорения, различные и по величине, и по направлению, вследствие чего расстояние между массами будет меняться, а относительное ускорение их уже не будет нулевым. Заметим, что, если пружины акселерометра имеют линейную характеристику, то величина ускорения каждой массы будет пропорциональна ее смещению относительно нулевого положения, соответствующего равномерному движению в однородном поле.

Рис. 2. Принципиальная схема спутникового градиентометра.

В условиях реального космического полета системы такого рода должны быть трехмерными (трехкомпонентными), т.е. пригодными для измерения по трем взаимно перпендикулярным базисным осям (рис.2б).

Важным аспектом, требующим отдельного рассмотрения, является то, что бортовые градиентометрические измерения выполняются во вращающейся системе отсчета, в то время как элементы тензора вторых производных гравитационного потенциала должны быть отнесены к «абсолютной» невращающейся системе координат, жестко связанной с Землей. Известно, что

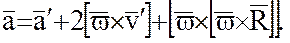(49)

В этой формуле обозначено:

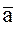- вектор ускорения пробной массы в «абсолютной» системе координат;

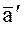- вектор ускорения той же массы во вращающейся системе координат;

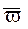- вектор угловой скорости вращения вращающейся системы координат;

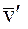- вектор линейной скорости пробной массы;

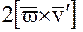- ускорение Кориоллиса;

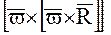- центробежное (переносное) ускорение.

В нашем случае в равномерно вращающейся с угловой скоростью 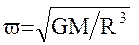орбитальной системе координат 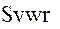вектор ускорения 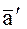, вектор угловой скорости 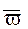, вектор линейной скорости и геоцентрический радиус-вектор 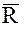пробной массы имеют вид:

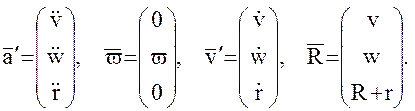
Выполняя в (49) операции векторного перемножения получим для ускорения Кориоллиса, возникающего вследствие одновременного вращения центра системы координат (центра масс спутника) и движения пробной массы относительно этого центра со скоростью :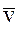

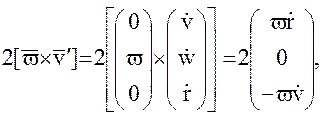
и центробежного ускорения

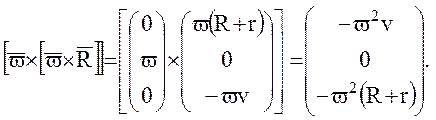
В итоге имеем для относящихся к абсолютной (не вращающейся) системе координат значений ускорений пробных масс 1 и 2 относительно центра масс спутника :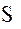

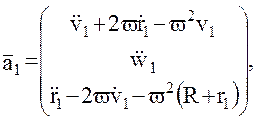
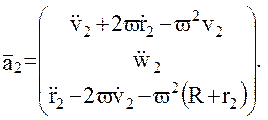
Тогда ускорение массы 2 относительно массы 1, по-прежнему записываемое в не вращающейся системе координат, имеет вид:

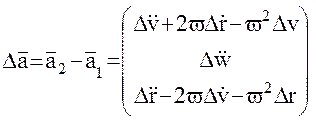
Заметим, кстати, что полученная нами здесь формула, по существу совпадает с формулой (14) пособия [1], поскольку обе они описывают компоненты вектора относительного ускорения двух вращающихся пробных масс. Учитывая (48), приходим к системе дифференциальных уравнений второго порядка:

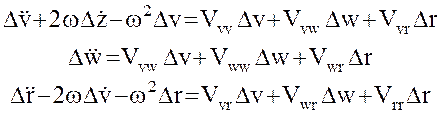(50)

Если входящие в (50) значения компонент вектора относительного ускорения 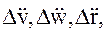вектора относительной скорости и вектора относительного положения 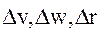двух пробных масс могут быть получены из измерений, выражение (50) можно рассматривать как систему трех уравнений для определения пяти независимых неизвестных значений вторых производных гравитационного потенциала.