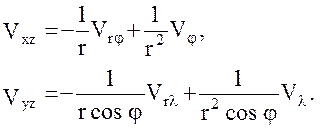В сферической системе координат.
В силу определения потенциальной функции 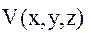 в системе координат
в системе координат  можем записать:
можем записать:
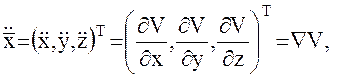 (5)
(5)
где 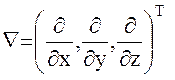 - векторный оператор Гамильтона (градиент).
- векторный оператор Гамильтона (градиент).
Повторное воздействие оператора Гамильтона на вектор (5) порождает матрицу (1) вторых производных гравитационного потенциала:
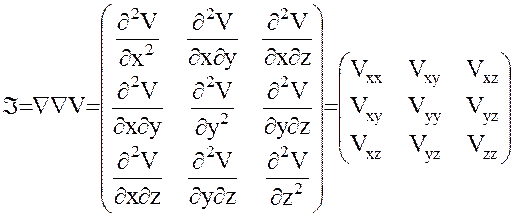 (1)
(1)
Основные затруднения при выводе соотношений спутниковой градиентометрии связаны с необходимостью представления компонент тензора (1) в сферических координатах, поскольку гравитационный потенциал, моделируемый рядом
объемных сферических функций:
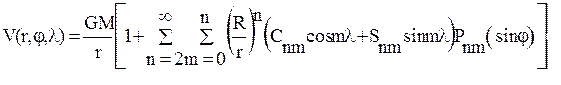 (6)
(6)
представляет собой функцию сферических координат. Учитывая это, запишем оператор Гамильтона в форме, обеспечивающей связь прямоугольных координат со сферическими:
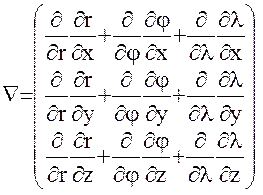 . (7)
. (7)
Однократное воздействие оператора (7) на скалярную функцию сферических координат (6) порождает вектор
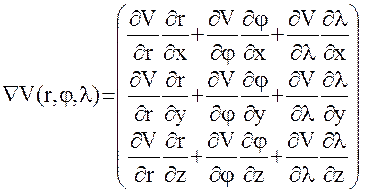 . (8)
. (8)
Повторное воздействие оператора Гамильтона, записанного в форме (7), на вектор (8) дает матрицу 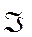 вторых производных гравитационного потенциала, элементы которой в отличие от (1) будут выражаться в виде производных по сферическим координатам. Вследствие громоздкости выкладок подробно рассмотрим процедуру вывода для одной из производных (например, для производной
вторых производных гравитационного потенциала, элементы которой в отличие от (1) будут выражаться в виде производных по сферическим координатам. Вследствие громоздкости выкладок подробно рассмотрим процедуру вывода для одной из производных (например, для производной 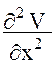 ), для других же элементов матрицы (1) приведем готовые формулы, которые могут быть получены читателем самостоятельно согласно излагаемому ниже алгоритму. Итак,
), для других же элементов матрицы (1) приведем готовые формулы, которые могут быть получены читателем самостоятельно согласно излагаемому ниже алгоритму. Итак,
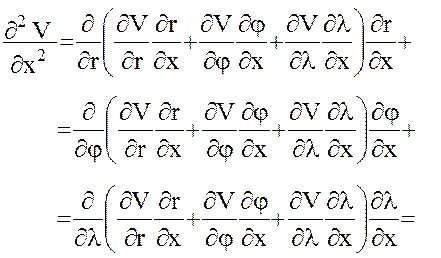
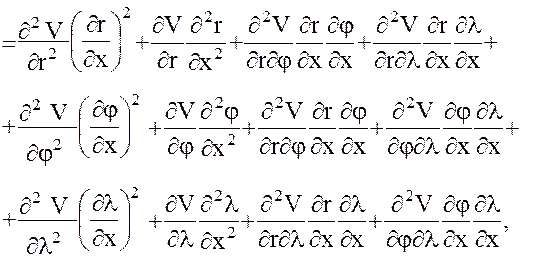
то есть
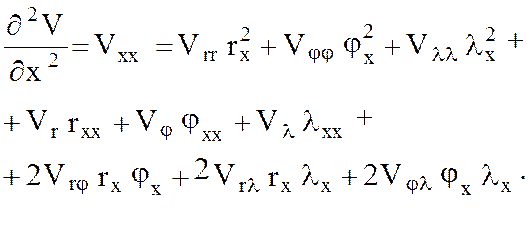 (9)
(9)
Аналогично получаем:
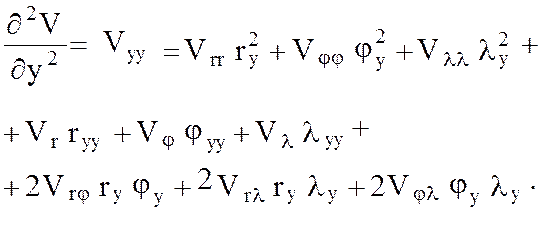 (10)
(10)
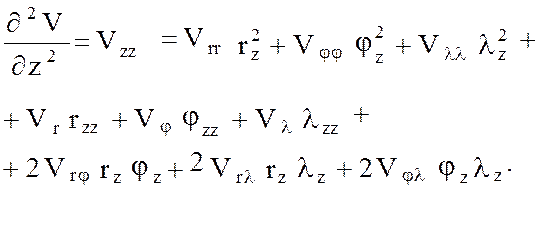 (11)
(11)
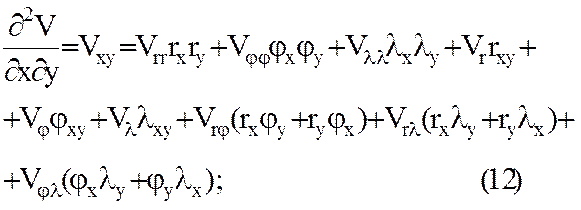
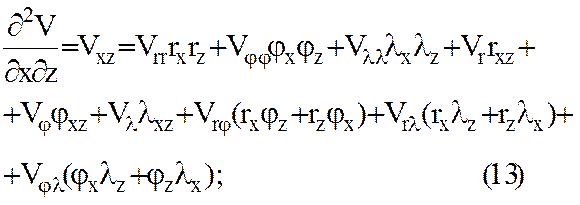
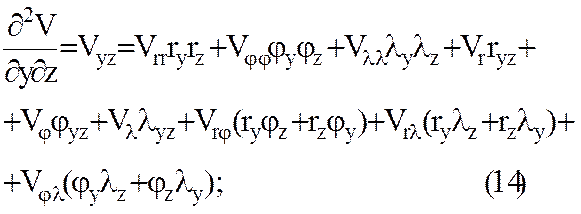
§ 3. Вычисление вторых производных потенциала
в горизонтной системе координат
Вычисление вторых производных гравитационного потенциала по формулам (9) – (14) продолжим следующим образом. Геоцентрические прямоугольные координаты 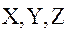 некоторой точки пространства связаны со сферическими координатами
некоторой точки пространства связаны со сферическими координатами 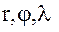 той же точки очевидными соотношениями
той же точки очевидными соотношениями
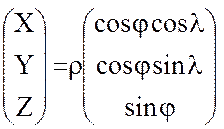 и
и 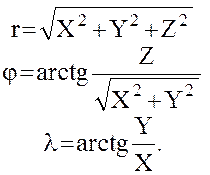 (15)
(15)
Далее, пользуясь рисунком 1, установим связь геоцентрической экваториальной системы координат  со спутникоцентрической горизонтной системой координат
со спутникоцентрической горизонтной системой координат 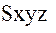 . В случае круговой орбиты приведение вектора
. В случае круговой орбиты приведение вектора 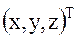 , описывающего положение точки в системе координат
, описывающего положение точки в системе координат 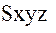 к вектору
к вектору 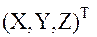 , описывающему положение той же точки в системе координат
, описывающему положение той же точки в системе координат  , достигается переносом центра системы и двумя поворотами осей:
, достигается переносом центра системы и двумя поворотами осей:
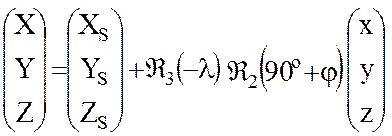 . (16)
. (16)
Первое вращение системы  вокруг оси
вокруг оси  на угол
на угол 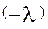 (напомним, что положительным считается вращение против часовой стрелки) приводит оси
(напомним, что положительным считается вращение против часовой стрелки) приводит оси
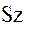 и
и 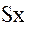 в плоскость
в плоскость 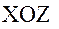 , т.е. в плоскость нулевого меридиана, от
, т.е. в плоскость нулевого меридиана, от
которого против часовой стрелки отсчитываются геоцентрические долготы
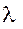 . Второе вращение вокруг оси
. Второе вращение вокруг оси 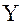 (или
(или 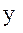 , поскольку после первого вращения направления осей
, поскольку после первого вращения направления осей 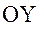 и
и 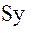 совпадают) против часовой стрелки
совпадают) против часовой стрелки
на угол 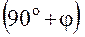 приводит к совпадению направлений осей
приводит к совпадению направлений осей 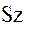 и
и 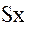 с осями
с осями 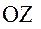 и
и 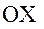 соответственно. Матрицы
соответственно. Матрицы 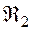 и
и 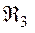 суть стандартные матрицы вращений вокруг осей 2 и 3.
суть стандартные матрицы вращений вокруг осей 2 и 3.
Раскрывая (16), получаем соотношения
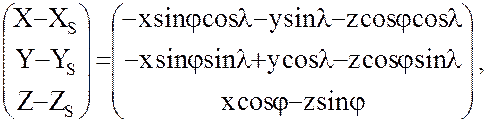 (17)
(17)
которые будут нами ниже использованы для вычисления входящих в выражения (9) – (14) производных. Эта процедура хотя и проста, но достаточно громоздка, что позволяет, подробно остановившись на вычислении одной из шести производных, (например, следуя сделанному ранее выбору, производной 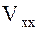 (9)), вывод формул для других производных снова рекомендовать читателю для самостоятельных упражнений в дифференцировании.
(9)), вывод формул для других производных снова рекомендовать читателю для самостоятельных упражнений в дифференцировании.
Обратимся далее к вычислению входящих в правую часть равенства (9) производных первого и второго порядков от сферических геоцентрических экваториальных координат 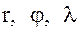 по прямоугольным спутникоцентрическим горизонтным координатам
по прямоугольным спутникоцентрическим горизонтным координатам 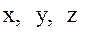 :
:
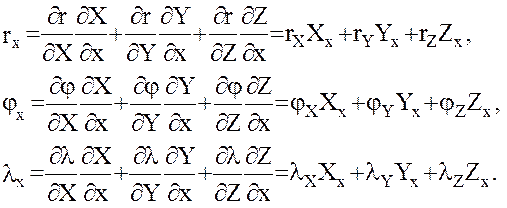 (18)
(18)
Вычисление вторых производных 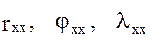 выполним путем дифференцирования равенств (18):
выполним путем дифференцирования равенств (18):
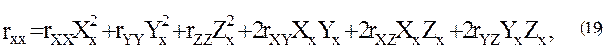
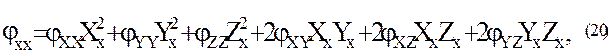
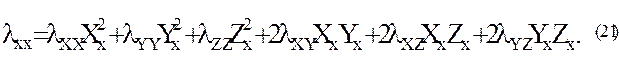
Прямое дифференцирование равенств (15) дает:
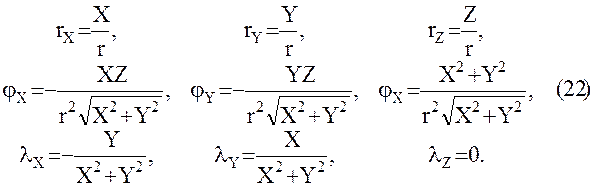
В свою очередь, дифференцируя формулу (17), получаем:
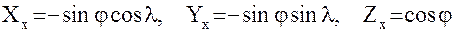 . (23)
. (23)
Тогда
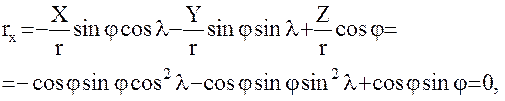
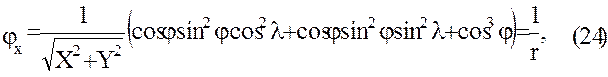
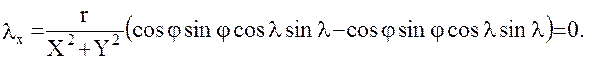
Дважды дифференцируя формулы (15), получим соотношения, позволяющие вычислить следующие вторые производные:
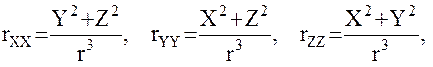
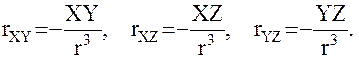 (25)
(25)
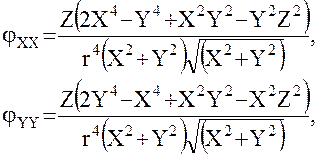
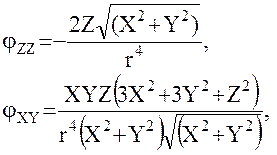 (26)
(26)
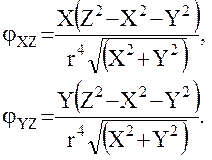
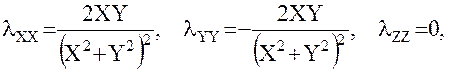
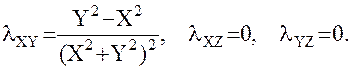 (27)
(27)
Формулы для вычисления входящих в (19) - (21) производных от геоцентрических прямоугольных координат по спутникоцентрическим прямоугольным координатам получим дифференцированием равенств (17):
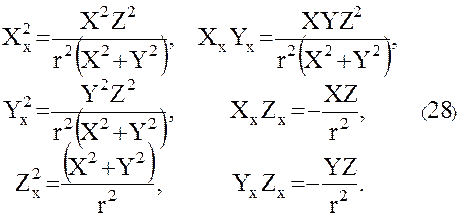
Подстановка (25) и (28) в (22) дает: 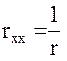 , подстановка (26) и (28) в (23) дает:
, подстановка (26) и (28) в (23) дает: 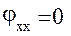 , подстановка (27) и (28) в (24) дает:
, подстановка (27) и (28) в (24) дает: 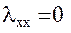 . Тогда выражение (9) после выполнения всех необходимых подстановок примет вид:
. Тогда выражение (9) после выполнения всех необходимых подстановок примет вид:
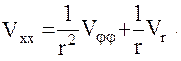
Приведем далее итоговую сводку формул, связывающих вторые производные гравитационного потенциала по осям горизонтной системы координат со вторыми его производными по сферическим координатам:
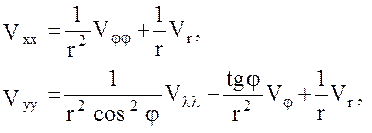
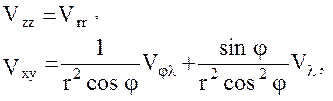 (29)
(29)