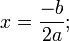Методические указания по выполнению отдельных разделов контрольно-курсовой работы
Ниже приведены алгоритмы решения заданий
| № Вар. | Название | Метод вычисления |
| Нахождение наибольшего общего делите (НОД) и наименьшего общего кратного (НОК) | Алгоритм Евклида для нахождения НОД: 1. большее число делим на меньшее 2. если делиться без остатка – это НОД 3. если есть остаток, то большее число заменяем на остаток от деления (r=a1-(a1/a1)a2) 4. переходим к пункту 1. Нахождение НОК: НОК( a , b) = a*b / НОД(a, b) | |
| Расширенный алгоритм Евклида | НА ВХОДЕ: два неотрицательных числа a и b: a>=bНА ВЫХОДЕ: d=НОД(a,b) и целые x,y: ax + by = d.1. Если b=0 положить d:=a, x:=1, y:=0 и возвратить (d,x,y)2. Присвоить x2:=1, x1:=0, y2:=0, y1:=13. Пока b>0 3.1 q:=[a/b], r:=a-qb, x:=x2-qx1, y:=y2-qy1 3.2 a:=b, b:=r, x2:=x1, x1:=x, y2:=y1, y1:=y4. Присвоить d:=a, x:=x2, y:=y2 и возвратить (d,x,y) | |
| Нахождение обратного элемента | Важно:Элемент a во множестве чисел n обратим тогда и только тогда, когда НОД(a,n)=1. То есть ответ есть не всегда. Из определения обратного элемента прямо следует алгоритм. НА ВХОДЕ: а из множества чисел n.НА ВЫХОДЕ: обратный к а в кольце, если он существует.1. Использовать расширенный алгоритм Евклида для нахождения x и y, таких что ax + ny = d, где d=НОД(a,n).2. Если d > 1, то обратного элемента не существует. Иначе возвращаем x. 4. Выход d,x,y такие что d=НОД(a,b)=ax+by | |
| Возведение в степень по модулю | 1. Присваиваем начальные значения переменным: S=1, V=W,c=a 2. Если V=0, то СТОП 3. Если значение V является нечетным (V mod 2=1), то присваиваем новые значения переменным: Z=Sc mod n (n - множество чисел) и V=(v-1)/2 и переходим к шагу 5. В противном случае переходим к шагу 4 4. Выполняем присваивание V=V/2 5. Выполняем присваивание c=c2 mod n 6. Переходим к шагу 2 ВЫХОД: Значение S=aW mod n | |
| Нахождение простых чисел в диапазоне от a до b | ВАЖНО:простым числом называется число, которое делится без остатка только на единицу и само на себя. 1. Определяется диапазон чисел 2. Используется алгоритм Евклида для нахождения наибольшего общего делителя (НОД)для чисел в диапазоне от а до и 3. Если НОД>1, то выполняется шаг 7 4. Для чисел проверяется отношение 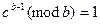 5. Если сравнение не выполняется, то переход к шагу 7 6. Выдается последовательность простых чисел 7. Выдается результат, что число составное 5. Если сравнение не выполняется, то переход к шагу 7 6. Выдается последовательность простых чисел 7. Выдается результат, что число составное | |
| Умножение матрицы на простое число | 1. Проверить является ли число простым (см. вариант 5) 2. Умножить матрицу на число (называемое скаляр). Если A — матрица  и x — скаляр, то C = xA — матрица и x — скаляр, то C = xA — матрица  , в которой , в которой 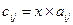 . 3. При делении . 3. При делении 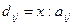 | |
| Умножение матриц | Две матрицы различного размера могут быть перемножены, если число столбцов первой матрицы совпадает с числом строк второй матрицы. Если A — матрица размера  , а матрица B размера , а матрица B размера  , то произведением будет матрица C размером , то произведением будет матрица C размером 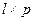 . Если элемент матрицы A обозначить . Если элемент матрицы A обозначить 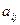 , а каждый элемент матрицы B обозначить , а каждый элемент матрицы B обозначить 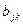 , то элемент матрицы C — , то элемент матрицы C — 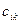 — вычисляется следующим образом: — вычисляется следующим образом: 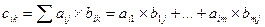 | |
| Нахождение определителя матрицы | Определитель (детерминант) — квадратная матрица A размера  , обозначаемая как det (A) — скалярное вычисление рекурсивно, как это показано ниже: 1. , обозначаемая как det (A) — скалярное вычисление рекурсивно, как это показано ниже: 1. 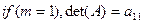 2. 2. 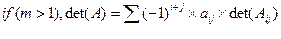 , где Aij получается из A удалением i -той строки j -того столбца. Детерминант определяется только для квадратной матрицы , где Aij получается из A удалением i -той строки j -того столбца. Детерминант определяется только для квадратной матрицы | |
| Решение квадратного уравнения вида ax2+bx+c=0 | 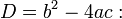
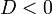 корней нет. корней нет. | |
| Сложение и вычитание матриц | Операция сложения двух матриц может применяться, если матрицы имеют одинаковое число столбцов и строк. Сложение записывают как C =A + B. В этом случае полученная в результате матрица C имеет тот же самый номер строк и столбцов, как A или B. Каждый элемент C — сумма двух соответствующих элементов A и B: 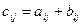 Операция вычитания производится аналогично сложению, за исключением того, что каждый элемент В вычитается из соответствующего элемента A: Операция вычитания производится аналогично сложению, за исключением того, что каждый элемент В вычитается из соответствующего элемента A: 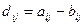 . . | |
| Нахождение частного решения уравнения вида ax=b(mod n) | Уравнение этого типа может не иметь ни одного решения или иметь ограниченное число решений. Предположим, что НОД (a, n) = d. Если d не делит b, решение не существует. Если d делит b, то имеется d решений. Если d делит b, то для того, чтобы найти решения, выполняются следующие действия: 1. Сократить уравнение, разделив обе стороны уравнения (включая модуль) на d. 2. Умножить обе стороны сокращенного уравнения на мультипликативную инверсию, чтобы найти конкретное решение x0. | |
| Программа нахождения частного решения линейных диофантовых уравнений ax+by=c | Найти значения целых чисел для x и y, которые удовлетворяют этому уравнению. Этот тип уравнения либо не имеет решений, либо имеет бесконечное число решений. Пусть d = НОД (a, b). Если d не делит c, то уравнение не имеет решения. Если d делит c, то мы имеем бесконечное число решений. Одно из них называется частным, остальные — общими. Частное решение Если d делит c, то можно найти частное решение вышеупомянутого уравнения, используя следующие шаги. 1. Преобразуем уравнение к a1x + b1y = c1, разделив обе части уравнения на d. Это возможно, потому, что d делит a, b, и c в соответствии с предположением. 2. Найти s и t в равенстве a1s + b1t = 1, используя расширенный алгоритм Евклида. 3. Частное решение может быть найдено: Частное решение: X0 = (c/d)s и y0 = (c/d) t | |
| Программа решения уравнения вида ax+c=b(mod n) | Сначала нужно привести уравнение к форме ax=b(mod n). Для этого к обеим сторонам уравнения прибавляется или отнимается число с. Затем выполняются действия из задания 11. | |
| Программа нахождения арифметической прогрессии | Арифметическая прогрессия — числовая последовательность вида 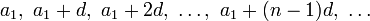 , то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа , то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа 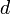 (шага или разности прогрессии): (шага или разности прогрессии): 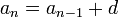 | |
| Программа нахождения геометрической прогрессии | Формула геометрической прогрессии для нахождения членов прогрессии 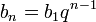 . Для решения задачи определить интервал чисел . Для решения задачи определить интервал чисел | |
| Сценарий сортировки методом пузырька | Алгоритм состоит из повторяющихся проходов по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются N-1 раз или до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При каждом проходе алгоритма по внутреннему циклу, очередной наибольший элемент массива ставится на своё место в конце массива рядом с предыдущим «наибольшим элементом», а наименьший элемент перемещается на одну позицию к началу массива | |
| Сценарий сортировки методом Шелла | При сортировке Шелла сначала сравниваются и сортируются между собой значения, стоящие один от другого на некотором расстоянии 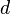 (о выборе значения (о выборе значения 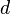 ). После этого процедура повторяется для некоторых меньших значений ). После этого процедура повторяется для некоторых меньших значений 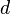 , а завершается сортировка Шелла упорядочиванием элементов при , а завершается сортировка Шелла упорядочиванием элементов при 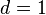 (то есть обычной сортировкой вставками). (то есть обычной сортировкой вставками). | |
| Сценарий сортировки вставками | На каждом шаге алгоритма мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированном списке, до тех пор, пока набор входных данных не будет исчерпан. Метод выбора очередного элемента из исходного массива произволен; может использоваться практически любой алгоритм выбора. Обычно (и с целью получения устойчивого алгоритма сортировки), элементы вставляются по порядку их появления во входном массиве | |
| Сценарий сортировки методом выбора | Исходный массив длиной N разбивается на две части: итог и остаток. Участок массива, называемый итогом, располагается с начала массива и должен быть упорядоченным, а участок массива, называемый остатком, располагается вплотную за итогом и содержит исходные числа не отсортированной части исходного массива | |
| Сценарий быстрой сортировки | Выбираем в массиве некоторый элемент, который будем называть опорным элементом. Известные стратегии: выбирать постоянно один и тот же элемент, например, средний или последний по положению; выбирать элемент со случайно выбранным индексом. Реорганизуем массив таким образом, чтобы все элементы со значением меньшим или равным опорному элементу, оказались слева от него, а все элементы, превышающие по значению опорный — справа от него. Обычный алгоритм операции: Два индекса — l и r, приравниваются к минимальному и максимальному индексу разделяемого массива, соответственно. Вычисляется индекс опорного элемента m. Индекс l последовательно увеличивается до тех пор, пока l-й элемент не окажется больше либо равен опорному. Индекс r последовательно уменьшается до тех пор, пока r-й элемент не окажется меньше либо равен опорному. Если r = l — найдена середина массива — операция разделения закончена, оба индекса указывают на опорный элемент. Если l < r — найденную пару элементов нужно обменять местами и продолжить операцию разделения с тех значений l и r, которые были достигнуты. Следует учесть, что если какая-либо граница (l или r) дошла до опорного элемента, то при обмене значение m изменяется на r-й или l-й элемент соответственно, изменяется именно индекс опорного элемента и алгоритм продолжает свое выполнение. Рекурсивно упорядочиваем подмассивы, лежащие слева и справа от опорного элемента. Базой рекурсии являются наборы, состоящие из одного или двух элементов. Первый возвращается в исходном виде во втором, при необходимости, сортировка сводится к перестановке двух элементов. Все такие отрезки уже упорядочены в процессе разделения. |
Оформление пояснительной записки
Пояснительная записка пояснительная записка набирается на компьютере в WORD(под Windows).
При использовании WORD, текст набирается шрифтом Times New Roman (Cyr) величиной 14 пунктов с одинарным интервалом. Формат бумаги - А4. Абзацный отступ - 1,25 см. Все поля страницы – по 2 см, переплет – 1 см. Текст на странице выравнивается по ширине.
Таблицы желательно располагать на странице без разрыва, а в случае переноса на другую страницу – дублируется шапка таблицы.
Рисунки располагаются по тексту пояснительной записки. В порядке исключения рисунки могут быть выполнены на отдельных листах белой бумаги, либо на кальке черной тушью или пастой. Рисунки имеют подрисуночную надпись и нумерацию – либо сквозную, либо по разделам.
Формулы следует выполнять в редакторе Microsoft Equation со следующими размерами:
обычный .................................... 18 пт;
крупный индекс ........................ 14 пт;
мелкий индекс .......................... 12 пт;
крупный символ ....................... 24 пт;
мелкий символ .......................... 10 пт.
Шрифты: Times New Roman (Cyr), Symbol.
Ссылки на литературу даются в квадратных скобках.
Желательно проверять орфографию и грамматику текста пояснительной записки перед распечаткой – для этого в редакторах имеются специальные опции!
Образец выполнения титульного листа прилагается (приложение 3).

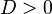 корней два, и они вычисляются по формуле:
корней два, и они вычисляются по формуле: 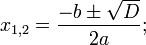 (1)
(1)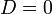 корень один :
корень один :