ГОСТ 28147-89. Режим гаммирования.

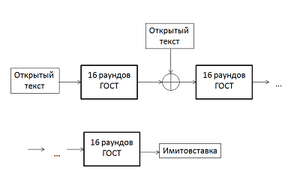
При работе ГОСТ 28147-89 в режиме гаммирования описанным ниже образом формируется криптографическая гамма, которая затем побитно складывается по модулю 2 с исходным открытым текстом для получения шифротекста. Шифрование в режиме гаммирования лишено недостатков, присущих режиму простой замены^[2]. Так, даже идентичные блоки исходного текста дают разный шифротекст, а для текстов с длиной, не кратной 64 бит, "лишние" биты гаммы отбрасываются. Кроме того, гамма может быть выработана заранее, что соответствует работе шифра в поточном режиме.

Выработка гаммы происходит на основе ключа и так называемой синхропосылки, которая задает начальное состояние генератора. Алгоритм выработки следующий:

1. Синхропосылка шифруется с использованием описанного алгоритма простой замены, полученные значения записываются во вспомогательные 32-разрядные регистры N₃ и N₄ - младшие и старшие биты соответственно.
2. N₃ суммируется по модулю 2³² с константой C₂ = 1010101₁₆
3. N₄ суммируется по модулю 2³²-1 с константой C₁ = 1010104₁₆
4. N₃ и N₄ переписываются соответственно в N₁ и N₂, которые затем шифруются с использованием алгоритма простой замены. Полученный результат является 64 битами гаммы.
5. Шаги 2-4 повторяются в соответствии с длиной шифруемого текста.

Для расшифровывания необходимо выработать такую же гамму, после чего побитно сложить её по модулю 2 с зашифрованным текстом. Очевидно, для этого нужно использовать ту же синхропосылку, что и при шифровании. При этом, исходя из требований уникальности гаммы, нельзя использовать одну синхропосылку для шифрования нескольких массивов данных. Как правило, синхропосылка тем или иным образом передается вместе с шифротекстом.

Особенность работы ГОСТ 28147-89 в режиме гаммирования заключается в том, что при изменении одного бита шифротекста изменяется только один бит расшифрованного текста. С одной стороны, это может оказывать положительное влияние на помехозащищённость; с другой - злоумышленник может внести некоторые изменения в текст, даже не расшифровывая его

Билет

1. ГОСТ 28147-89. Режим выработки имитовставки.

Этот режим не является в общепринятом смысле режимом шифрования. При работе в режиме выработки имитовставки создаётся некоторый дополнительный блок, зависящий от всего текста и ключевых данных. Данный блок используется для проверки того, что в шифротекст случайно или преднамеренно не были внесены искажения. Это особенно важно для шифрования в режиме гаммирования, где злоумышленник может изменить конкретные биты, даже не зная ключа; однако и при работе в других режимах вероятные искажения нельзя обнаружить, если в передаваемых данных нет избыточной информации.

Имитовставка вырабатывается для M ≥ 2 блоков открытого текста по 64 бит. Алгоритм следующий:

1. Блок открытых данных записывается в регистры N₁ и N₂, после чего подвергается преобразованию, соответствующему первым 16 циклам шифрования в режиме простой замены
2. К полученному результату побитно по модулю 2 прибавляется следующий блок открытых данных. Последний блок при необходимости дополняется нулями. Сумма также шифруется в соответствии с пунктом 1.
3. После добавления и шифрования последнего блока из результата выбирается имитовставка длиной L бит: с бита номер 32-L до 32 (отсчёт начинается с 1). Стандарт рекомендует выбирать L исходя из того, что вероятность навязывания ложных данных равна 2^-L. Имитовставка передается по каналу связи после зашифрованных блоков.

Для проверки принимающая сторона после расшифровывания текста проводит аналогичную описанной процедуру. В случае несовпадения результата с переданной имитовставкой все соответствующие M блоков считаются ложными.

Следует отметить, что выработка имитовставки может проводиться параллельно шифрованию с использованием одного из описанных выше режимов работы

2. Алгоритм Диффи-Хеллмана

Предположим, что обоим абонентам известны некоторые два числа g и p, которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение A = g^amod p и пересылает его второму, а второй вычисляет B = g^bmod p и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение B^amod p = g^abmod p, а второй абонент на основе имеющегося у него b и полученного по сети A вычисляет значение A^bmod p = g^abmod p. Как нетрудно видеть, у обоих абонентов получилось одно и то же число: K = g^abmod p. Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления g^abmod p по перехваченным g^amod p и g^bmod p, если числа p,a,b выбраны достаточно большими.

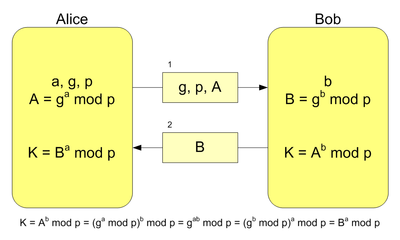
Алгоритм Диффи — Хеллмана, где K — итоговый общий секретный ключ

При работе алгоритма, каждая сторона:

1. генерирует случайное натуральное число a — закрытый ключ
2. совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где

p является случайным простым числом

g является первообразным корнем по модулю p

1. вычисляет открытый ключ A, используя преобразование над закрытым ключом

A = g^a mod p

1. обменивается открытыми ключами с удалённой стороной
2. вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a

K = B^a mod p

К получается равным с обоих сторон, потому что:

B^a mod p = (g^b mod p)^a mod p = g^ab mod p = (g^a mod p)^b mod p = A^b mod p

В практических реализациях, для a и b используются числа порядка 10¹⁰⁰ и p порядка 10³⁰⁰. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.

3. Схема шифрования Эль Гамаля.

Асимметричный алгоритм, предложенный в 1985 году Эль-Гамалем (T. ElGamal), универсален. Он может быть использован для решения всех трех основных задач: для шифрования данных, для формирования цифровой подписи и для согласования общего ключа. Кроме того, возможны модификации алгоритма для схем проверки пароля, доказательства идентичности сообщения и другие варианты. Безопасность этого алгоритма, так же как и алгоритма Диффи-Хеллмана, основана на трудности вычисления дискретных логарифмов. Этот алгоритм фактически использует схему Диффи-Хеллмана, чтобы сформировать общий секретный ключ для абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ.

И в случае шифрования, и в случае формирования цифровой подписи каждому пользователю необходимо сгенерировать пару ключей. Для этого, так же как и в схеме Диффи-Хеллмана, выбираются некоторое большое простое число Р и число А, такие, что различные степени А представляют собой различные числа по модулю Р. Числа Р и А могут передаваться в открытом виде и быть общими для всех абонентов сети.

Затем каждый абонент группы выбирает свое секретное число Х_i, 1 < Х_i < Р-1, и вычисляет соответствующее ему открытое число 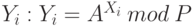. Таким образом, каждый пользователь может сгенерировать закрытый ключ Х_i и открытый ключ Y_i.

Информация о необходимых параметрах системы сведена в следующую таблицу.

	Общие параметры	Открытый ключ	Закрытый ключ
Пользователь 1	Р, А	Y1	Х1
…	…	…
Пользователь i	Yi	Хi

Шифрование

Теперь рассмотрим, каким образом производится шифрование данных. Сообщение, предназначенное для шифрования, должно быть представлено в виде одного числа или набора чисел, каждое из которых меньше Р. Пусть пользователь 1 хочет передать пользователю 2 сообщение m. В этом случае последовательность действий следующая.

1. Первый пользователь выбирает случайное число k, взаимно простое с Р-1, и вычисляет числа

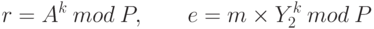
где Y₂ – открытый ключ пользователя 2. Число k держится в секрете.

1. Пара чисел (r, е), являющаяся шифротекстом, передается второму пользователю.
2. Второй пользователь, получив (r,e), для расшифрования сообщения вычисляет

где Х₂ – закрытый ключ пользователя 2. В результате он получает исходное сообщение m.

Если злоумышленник узнает или перехватит Р, А, Y₂, r, e, то он не сможет по ним раскрыть m. Это связано с тем, что противник не знает параметр k, выбранный первым пользователем для шифрования сообщения m. Вычислить каким-либо образом число k практически невозможно, так как это задача дискретного логарифмирования. Следовательно, злоумышленник не может вычислить и значение m, так как m было умножено на неизвестное ему число. Противник также не может воспроизвести действия законного получателя сообщения (второго абонента), так как ему не известен закрытый ключ Х₂ (вычисление Х₂ на основании Y₂ — также задача дискретного логарифмирования).

По аналогичному алгоритму может производиться и согласование ключа, используемого для симметричного шифрования больших объемов данных. Более того, алгоритм Эль-Гамаля на практике целесообразно использовать именно для согласования общего ключа сессии, а не прямого шифрования больших сообщений. Это связано с тем, что в алгоритме используются операции возведения в степень и умножения по большому модулю. Так же как и в алгоритмах RSA и Диффи-Хеллмана, операции производятся над большими, состоящими из нескольких сотен или тысяч бит, числами. Поэтому шифрование больших сообщений производится крайне медленно.

Билет

1. Безопасные хэш-функции. Функции хэширования.

Хэш-функция — это преобразование, получающее из данных произвольной длины некое значение (свертку) фиксированной длины. Простейшими примерами являются контрольные суммы (например, crc32). Бывают криптографические и программистские хэши. Криптографический хэш отличается от программистского следующими двумя свойствами: необратимостью и свободностью от коллизий. Обозначим m – исходные данные, h(m) – хэш от них. Необратимость означает, что если известно число h0, то трудно подобрать m такое, что h(m) = h0. Свободность от коллизий означает, что трудно подобрать такие m1 и m2, что m1 не равно m2, но h(m1) = h(m2).

Криптографические хэш-функции разделяются на два класса:

• хэш-функции без ключа (MDC (Modification (Manipulation) Detect Code) - коды),
• хэш-функции c ключом (MАC (Message Authentication Code) - коды).
• Хэш-функции без ключа разделяются на два подкласса:
• слабые хэш-функции,
• сильные хэш-функции.

Слабой хэш-функцией называется односторонняя функция H(x), удовлетворяющая следующим условиям:

1. аргумент x может быть строкой бит произвольной длины;
2. значение H (x)должно быть строкой бит фиксированной длины;
3. значение H (x)легко вычислить;
4. для любого фиксированного x вычислительно невозможно найти другой x'!=x, такой что H(x')=H(x). Пара x'!=x, когда H(x')=H(x)называется коллизией хэш-функции.

Сильной хэш-функцией называется односторонняя функция H(x), удовлетворяющая условиям 1–3 для слабой хэш-функции и свойству 4': 4') вычислительно невозможно найти любую пару x'!=x, такой что H(x')=H(x).

Поскольку из свойств 1–2 следует, что множество определения хэш-функции значительно шире множества значений, то коллизии должны существовать. Свойство 4 требует, чтобы найти их для заданного значения х было практически невозможно. Требование 4' говорит о том, что у сильной хэш-функции вычислительно невозможно вообще найти какую-либо коллизию.

Хэш-функцией с ключом (MAC) называется функция H(k,x), удовлетворяющая свойствам:

1. аргумент хфункции H(k, x)может быть строкой бит произвольной длины;
2. значение H(k, x)должно быть строкой бит фиксированной длины;
3. при любых kи xлегко вычислить H(k, x);
4. для любого хдолжно быть трудно вычислить H(k, x),не зная k;
5. должно быть трудно определить kдаже при большом числе неизвестных пар {x, H(k, x)}при выбранном наборе хили вычислить по этой информации H(k, x')для x'!=x.

Зачем нужна хэш-функция? Дело в том, что многие криптографические преобразования (в частности, вычисление и проверка электронной цифровой подписи, ЭЦП) выполняются над данными фиксированного размера. Поэтому перед просталением электронной подписи под многомегабайтным файлом обычно рассчитывают значение хэш-функции от него, а уже от этого значения считают ЭЦП. Кроме того, удобно, например, пароли в базе хранить не в открытом виде, а в хэшированном (так сделано во всех юниксах).

Некоторые алгоритмы хэш-функций:

• MD 2.Message Digest. Алгоритм криптографической сверки. Порождает 128- bit блок от сообщения произвольной длины.
• MD 4.Другой алгоритм свертки. Порождает 128-bit блок.
• MD 5.Существенно переделанный MD 4. Автор тот же – Риверст.
• SHA.Результирующий хэш равен 160-bit.
• ГОСТ Р34.11–94.Российский алгоритм. Длина свертки – 256 бит (очень удобно для формирования по паролю ключа для ГОСТ 28147–89).

2. Алгоритм SHA.