DES стандарт. Режим с обратной связью по шифртексту.

Режим обратной связи по шифротексту (CFB — Cipher Feed Back) (см. Рис.9). В режиме СFB вырабатывается блочная «гамма» Z₀,Z₁,...Z_i = DESk(C_{i - 1})

. Начальный вектор C₀ сохраняется в секрете.

Расширенный алгоритм Евклида.

Расширенный алгоритм Евклида

Для различных приложений очень важно уметь представлять наибольший общий делитель целых чисел а и b в виде (теорема 2.2.3). Очевидно, один из способов состоит в применении алгоритма Евклида и затем «обратного» прохода. Например, для получаем

откуда следует, что 18 — наибольший общий делитель чисел 612 и 342. Проведя вычисления в обратном порядке, получим

т.е. и мы решили нашу задачу.

Другой подход к решению этой задачи, имеющий, как мы убедимся в дальнейшем, много приложений, состоит в применении расширенного алгоритма Евклида. Значения вычисляются в серии шагов, в каждом из которых мы выражаем а, - (вычисленное в процессе работы алгоритма Евклида, разд. 2.2.2) в форме

А именно рассмотрим последовательность

В левом столбце — последовательность делений, которая нам уже встречалась раньше и которая теперь разрешена относительно остатков. В правом столбце каждый остаток выражен в виде мы хотим вычислить Очевидно, что Сравнивая обе части на шаге, имеем откуда получается следующая индуктивная процедура вычисления

Конечно, мы мажем также вычислить как но приведенное выше выражение подчеркивает, что вычислено таким же способом, как Мы получили следующий алгоритм.

ХБА. Расширенный алгоритм Евклида (Extended Euclidean Algorithm)

Вход:

Выход: такие, что

1. [Инициализация]

2. [Основной цикл] Пока выполнять

3. [Выход] Вернуть

Анализ времени работы аналогичен проведенному для ЕА, детали мы оставляем читателю. Применяя расширенный алгоритм Евклида в нашем примере получим:

Заметим, что равенство выполняется на каждом шаге. Алгоритм выдает проверим ответ:

Билет

Китайская теорема об остатках.

Китайская теорема об остатках (CRT — Chinese Reminder Theorem) используется, чтобы решить множество уравнений с одной переменной, но различными взаимно простыми модулями, как это показано ниже:

Китайская теорема об остатках утверждает, что вышеупомянутые уравнения имеют единственное решение, если модули являются взаимно простыми.

Пример 12.35

Следующий пример содержит систему уравнений с различными модулями:

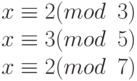
Для этой системы уравнений x = 23. Это значение удовлетворяет все уравнения: , , .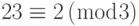

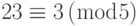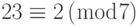Решение

Решение системы уравнений выполняется в следующем порядке:

1. Найти . Это общий модуль.
2. Найти M₁ = M/m₁, M₂ = M/m₂,…., M_k = M/m_k.
3. Используя соответствующие модули m₁, m₂,…., m_k, найти мультипликативную инверсию M₁, M₂,…, M_k. Обозначим ее M₁^-1, M₂^-1,…, M_k^-1.
4. Решение системы уравнений

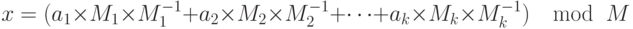
Обратите внимание, что система уравнений может иметь решение, даже если модули не взаимно простые. Однако в криптографии мы интересуемся только решением уравнений с взаимно простыми модулями.

Пример 12.36

Найдите решение системы уравнений

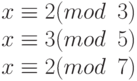
Из предыдущего примера мы уже знаем, что ответ x = 23. Определим его в четыре шага.

Решение

1. 
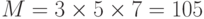
2. M₁ = 105/3 = 35, M₂ = 105/5 =21, M₃ = 105/7 = 15
3. Инверсии M₁^-1 = 2, M₂^-1 = 1, M₃^-1 = 1
4. 

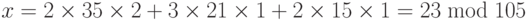
Пример 12.37

Найти целое, которое дает в остатке 3, если его разделить на 7 и 13, но без остатка делится на 12.

Решение

Это проблема китайской теоремы об остатке. Мы можем составить три уравнения и найти значение x.

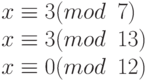
Если проведем четыре шага, мы найдем x = 276. Можем проверить, что 276 = 3 mod 7, 276 = 3 mod 13 и 276 делится на 12 (частное 23 и остаток 0).

Приложения

Китайская теорема об остатках часто применяется в криптографии. Одно из таких применений – решение квадратных уравнений — будет обсуждаться в следующей секции. Другое приложение — представление очень большого числа в виде списка малых целых чисел.

Пример 12.38

Предположим, нам надо вычислить z = x + y, где x = 123 и y = 334, но система принимает только числа меньше 100. Эти числа можно представить следующими уравнениями:

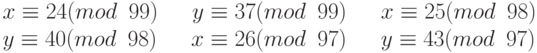
Сложим каждое уравнение x с соответствующим уравнением y:

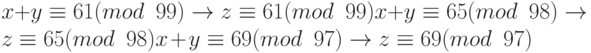
Теперь эти три уравнения могут быть решены, используя китайскую теорему об остатках, чтобы найти z. Один из приемлемых ответов равен z = 457.

Квадратичные вычеты.

В уравнении 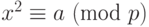. a называется квадратичным вычетом (QR), если уравнение имеет два решения; a называется квадратичным невычетом (QNR), если уравнение не имеет решений. Может быть доказано, что в Z_P* с p – 1 элементами (p – 1)/2 элементов — квадратичные вычеты и (p – 1)/2 являются квадратичными невычетами.

Пример 13.3

Есть 10 элементов в Z_11*. Пять из них – квадратичные вычеты, и пять — невычеты. Другими словами, Z_11* может быть разделен на два отдельных множества, QR и QNR, как это показано на рис. 13.1.